Fluid Mechanics and Machinery: Unit 3: Dimensional Analysis and Model Studies
Solved Examples Based on Model Analysis
Fluid Mechanics
Solved Examples Based on Model Analysis: Dimensional Analysis and Model Studies - Fluid Mechanics and Machinery
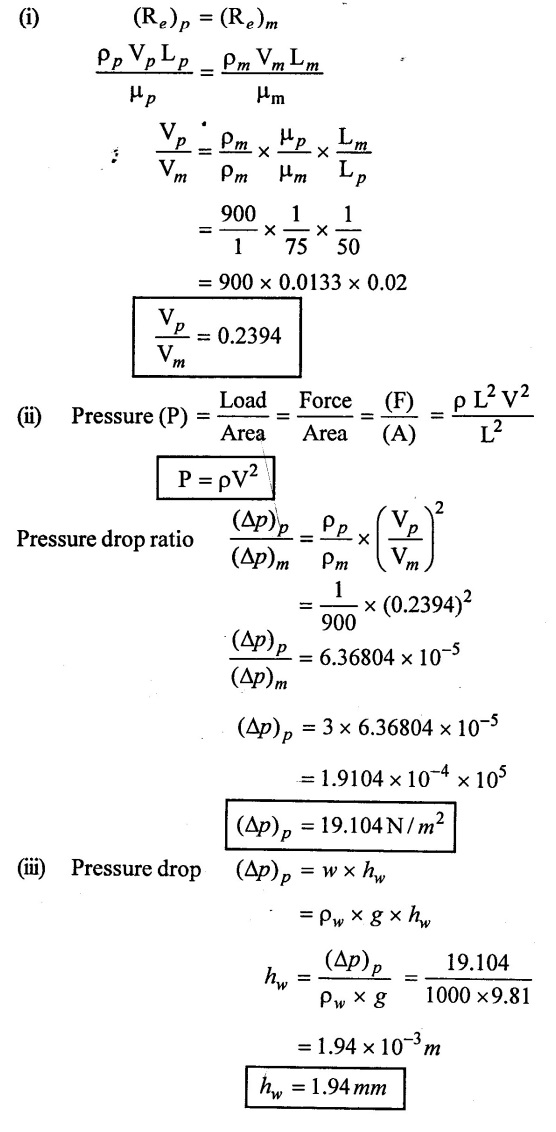
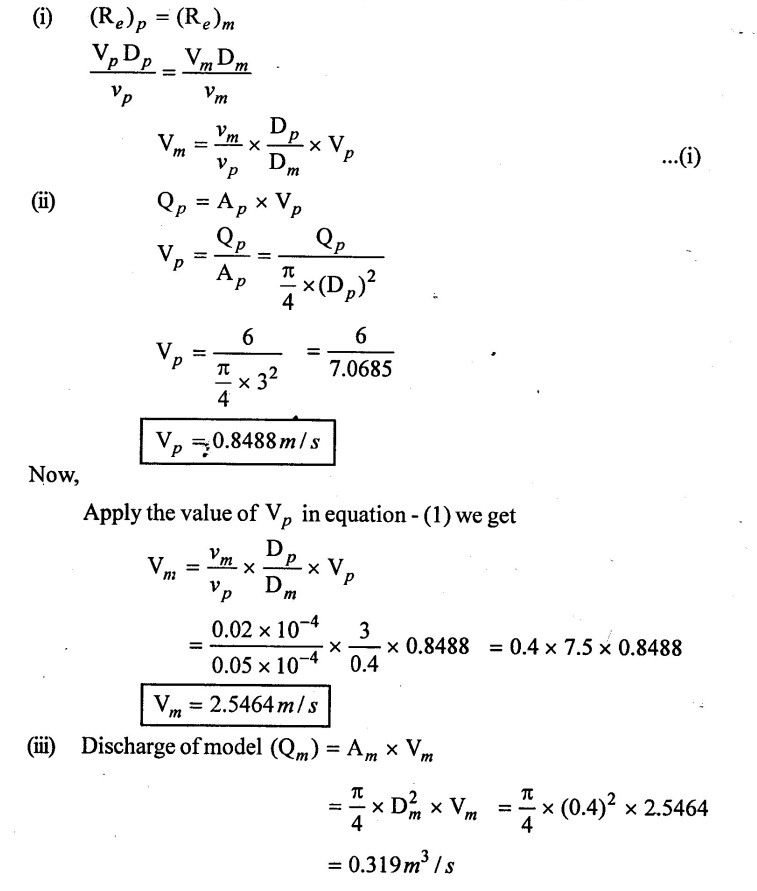
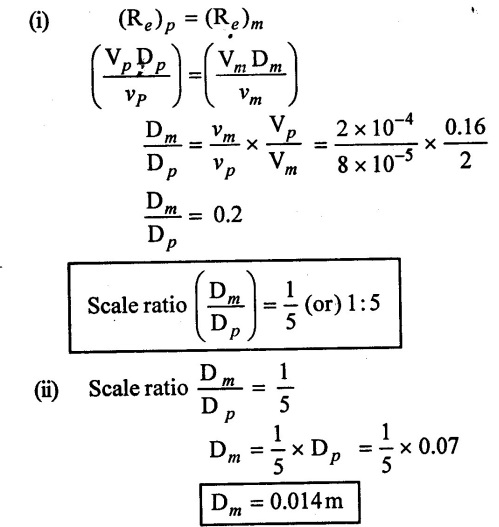
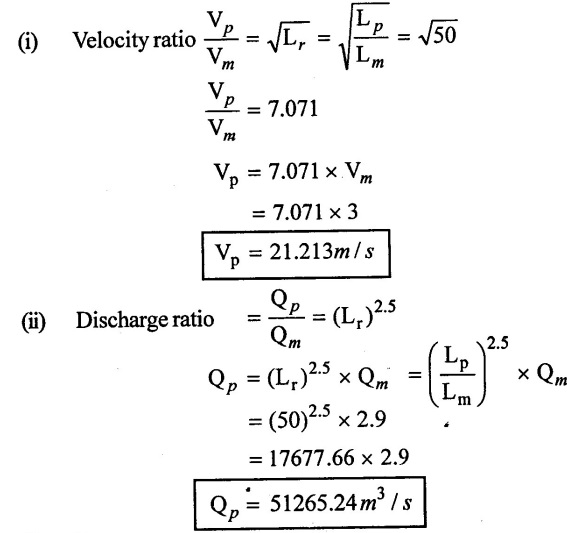
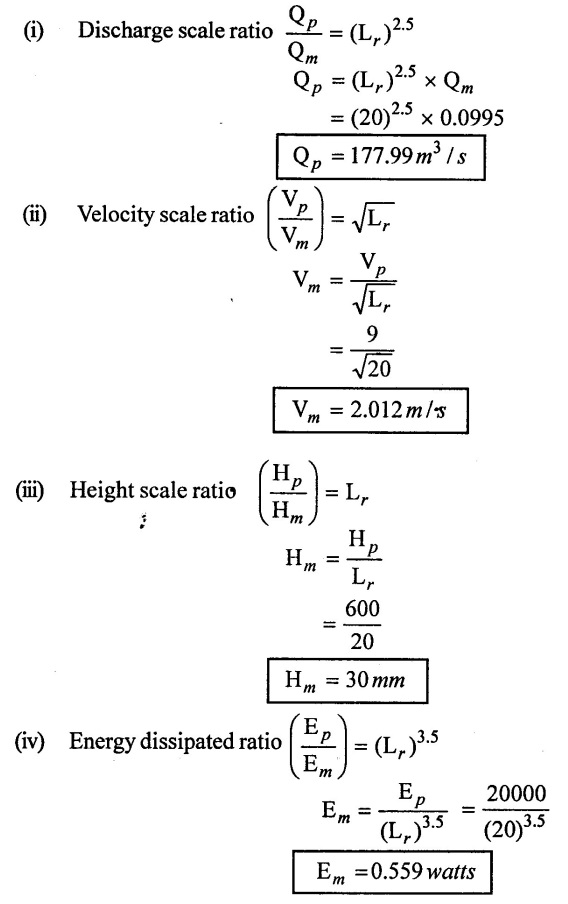
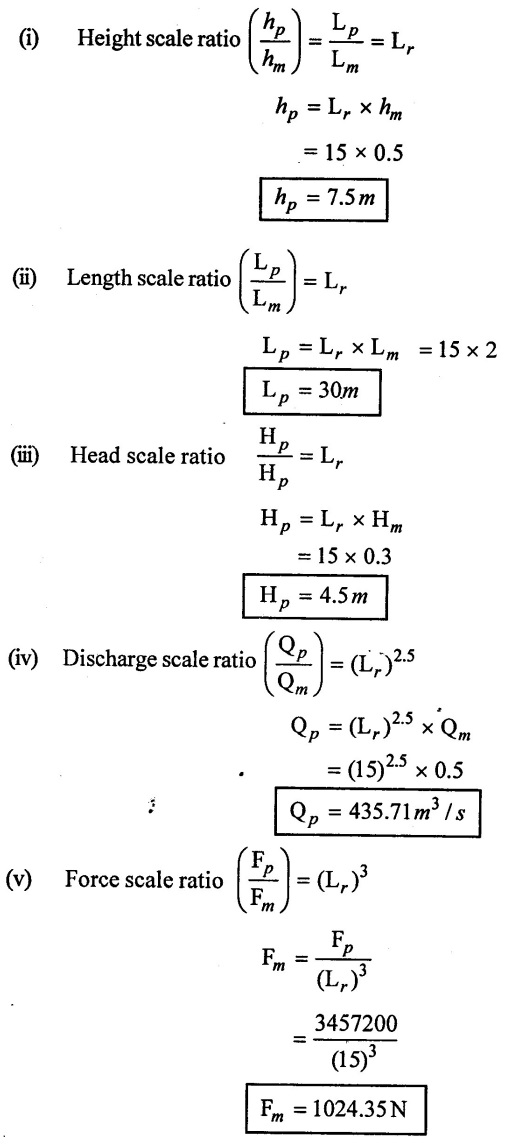
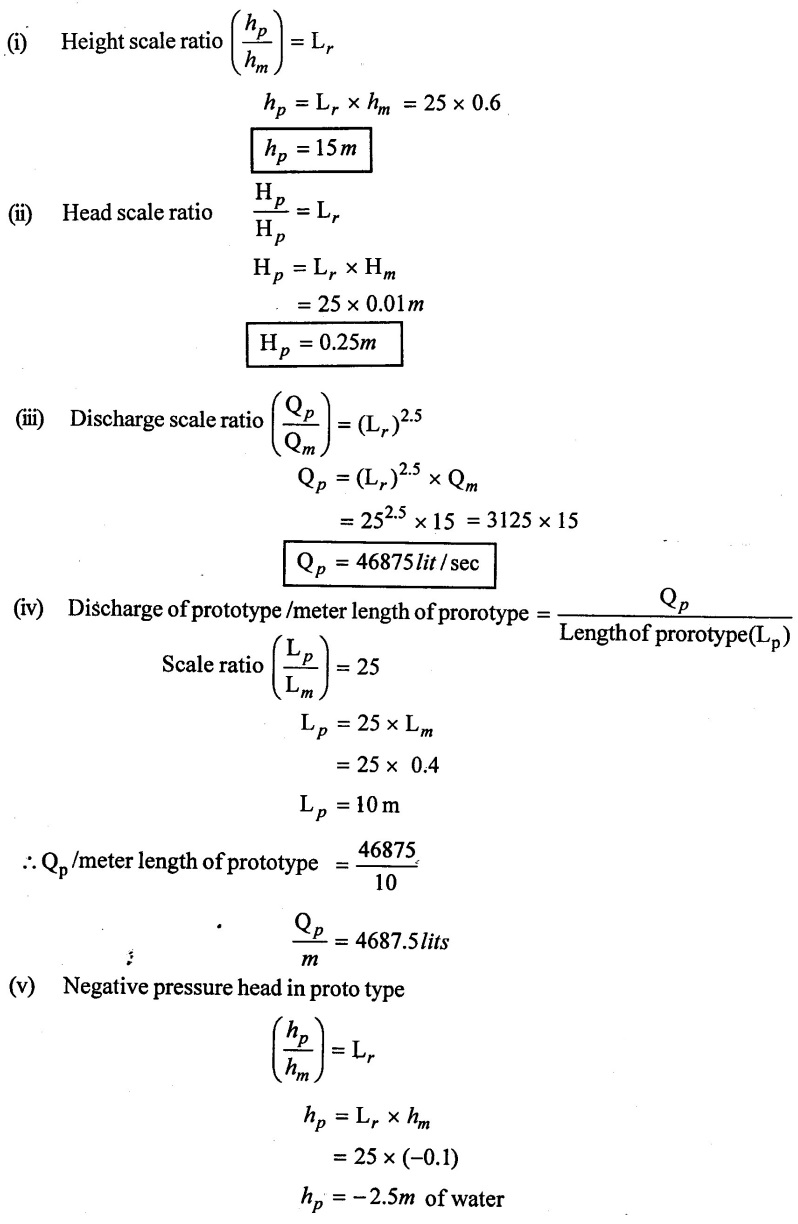
SOLVED EXAMPLES BASED ON MODEL ANALYSIS Example - 23 A pipe of diameter 2m is required to transport a lubricating oil of specific gravity 0.8 and dynamic viscosity 5×10-2 poise at the rate of 0.5m3/s. Test were conducted in model pipe of 0.3m diameter using water as a flowing medium and viscosity of water is 2 × 10-2 poise. Find the velocity and rate of flow in the model. Given data: To find: (i) Velocity (Vm) (ii) Rate of flow (Qm) Solution: (i) Given problem is based on closed pipe flow. So here using Reynolds's model law. (ii) Reynolds's model law says that Reynolds number in the model and prototype are equal. (i.e) (Re)model = (Re)prototype (iii) Hence (iv) Rate of flow in prototype (v) Vm = 13.334 × Vp = 13.334 × 0.159 (vi) Rate of flow in model Result : (i) Velocity (Vm) = 2.122 m/s (ii) Rate of flow (Qm) = 0.1499m3/s Example - 24 Oil is flowing through a pipe of diameter 40cm at a velocity of 6m/s. Find the velocity of water flowing in another pipe of diameter 15cm. If the condition of dynamic similarity is satisfied between the two pipes. The viscosity of oil and water is given as 0.002Ns/m2 and 0.0045 Ns/m2 respectively. The specific gravity of oil is 0.7. Given data: To find: Velocity of pipe at -2 Solution In this case fluid flow in closed pipe so apply Reynolds model law. Result, Velocity of pipe at 2 (V2) = 25.2 m/s Example - 25 The ratio of lengths of a air planes (prototype) and its model is 40:1 the speed of air planes is 15m/s. The model is to be tested in a wind tunnel. Find the speed of the air in wind tunnel. Also determine the ratio of the drag force between the model and its prototype. Take the value of kinematic viscosity for atmosphere air and wind tunnel air are 0.013 stokes and 0.017 stokes respectively and also density of air as 1.24kg/m3 same for model and prototype. Given data: To find: (i) Velocity of model (ii) Ratio of drag force between model Solution: In this case for airplanes, apply reynolds model law Result: (i) Velocity of model (Vm) = 784.61 m/s (ii) Ratio of Resistance force Example - 26 A ship 400m long moves in sea-water, whose density 1050 kg/m3. The ratio between model and prototype are 1:200 respectively of this ship is to be tested in a wind tunnel. The velocity of air in the wind tunnel around the model is 40m/s and resistance of the model is 80N. Determine the velocity of ship in sea-water and also the resistance of the ship in sea-water. The density of air is given as 1.24kg/m3. Take the kinematic viscosity of sea-water and air as 0.015 stokes and 0.019 strokes respectively. Given data: To find: Solution: In this case for ship, apply the Reynold's model law (iii) Resistance (F) = Mass × Acceleration Result, (i) Velocity of prototype (Vp) = 0.1578 m/s (ii) Resistance of prototype (Fp) = 42170.56 N. Example - 27 A model of an air duct is built to 1/50 scale is geometrically similar and tested with water which is 75 times more viscosity and 900 times density than air. When tested under dynamically in similar conditions, the pressure drop is 3 bar in model. Find corresponding pressure drop in prototype an express in water column. Given data: Pressure drop in model (Δp)m = 3 bar To find: Pressure drop in prototype (Δp)p Solution: In this case for air duct, apply Reynolds's model law (Re)p = (Re)m Result Pressure drop in mm of water column (hw) = 1.94 mm. Example - 28 A torpedo shaped object, 700mm diameter us to move in air at 50 m/s and its drag is to be estimated from tests in water on a 1th/4 of the scale model. Determine the 4 necessary speed of the model and the drag of the full scale object if that of the model is 900N. The viscosity of air and water are 1.76 × 10-5 Ns/m2 and 1.06 × 103 Ns/m2 respectively. Take ρair = 1.24kg/m3 and ρwater = 1000 kg/m3. Given data: To find: (i) Speed of the model (Vm) (ii) Dray force of the prototype (FD)p Solution: In this case for air duct, apply Reynolds model law Result (i) Velocity of model (Vm) = 14.936 m/s (ii) Drag force in prototype (FD)p = 200.103 N Example - 29 A 1:20 model of a car is tested in a wind tunnel. The car velocity is 90 kmph. If the drag is 500N. What is the drag and power required to over come the drag in the model. Assume dynamic viscosity and density of air for model and prototype to be same. Given data: To find (i) Drag force in the model (FD)m (ii) Power required in the model (Pm) Solution In this case the car is tested in a wind tunnel. So here Reynolds model law is applied. Result: (i) Drag force in the model (FD)m = 500N (ii) Power required in the model (Pm) =250 Kw. Example - 30 A pipe of 3m diameter is transporting oil of kinematic viscosity v = 0.05 stroke at a rate of 6000 Lps. If a 0.4m diameter pipe with water having v = 0.02 stroke is used for model testing, velocity and rate of flow in the model. Given data: To find: (i) Velocity of model (Vm) (ii) Rate of flow of model (Qm) Solution: In this case for closed pipe Reynolds model law is applied. Result: (i) Velocity of model (Vm) = 2.5464 m/s (ii) Discharge of model (Qm) = 0.379m3 / s Example - 31 The velocity of water in the model is 2 m/s through circular pipe and velocity of oil in the prototype is 0.16 m/s through 70 mm diameter pipe. Assume kinematic viscosity of water 2 × 10-4m2/s and that of oil is 8 × 10-5 m2/s. Find the scale ratio and diameter of the model pipe. Given data: To find : (i) Scale ratio (ii) Diameter of model (Dm). Solution: In this case for closed pipe, Reynolds model law is applied. Result: Example - 32 A ship has a length of 200m and area 5000m2. A model of this ship 10m in length. When towed in fresh water density and viscosity are 1000kg/m3 and 2 × 10-2 poise respectively. Velocity of model is 3 m/s produces at a resistance of 50 N. Calculate (i) Speed of the ship (prototype) (ii) Shaft power required to propel the ship at this speed through sea water of ρ = 1030kg/m2 and μ = 5 × 10-2 poise. Take propeller efficiency as 80 %. Given data: To find: (i) Speed of the ship (Vp) (ii) Shaft power (or) power input (Pp) Solution: In this case for ship motion, Reynolds model law is applied. Result: (i) Velocity of ship (Vp) = 0.36375 m/s (ii) Shaft power required (Pi) = 137.705 watts. Example - 33 In the model test of a spill way the discharge per meter length is 1/8m3 / sec. If the scale of the model is 1/64. Find the discharge per meter run of the prototype. Given data: To find: Discharge of the prototype per mete length Solution: In this case for spill way. So Froude's model law is applied. Discharge of prototype per metre length (qp) = 64 m3/s/m Example - 34 In 1 in 50 model of a spillway, the velocity and discharge are 3 m/s and 2.9m3/s. Find the velocity and discharge in the prototype. Given data: Scale ratio Velocity of model (Vm) = 3 m/s Discharge of model (Qm) = 2.9m3 / s To find: (i) Discharger of prototype (Qp) Velocity of prototype (Vp) Solution: In this case for spillway, frounde's model law is applied. Result: (i) Velocity in prototype (Vp) =21.213 m/s (ii) Discharge in prototype (Qp) = 51265.24 m3 / s Example - 35 A ship model of scale 1/75 is towed through sea water at a speed of 2 m/s. A force of 3N is required to tow the model. Determine the speed of ship and the propulsive force on the ship, if prototype is subjected to wave resistance only. Given data: Scale ratio Speed of model (Vm) = 2m/s Force required on model (Fm) = 3N To find: (i) Speed of ship prototype (Vp) (ii) Propulsive force (Fp) Solution: In this case, ship is subjected to wave resistance only. So froude's model law is applied here Result: (i) Speed of ship (Vp) = 17.32 m/s (ii) Propulsive force of ship (Fp) = 1.265 × 106 N Example - 36 The characteristics of the spillway are to be studied by means of a geometrically similar model constructed to the scale ratio 1:20. The flow rate in the model is 0.0995 cumecs and the velocity, high and energy disipated in the prototype are 9 m/s, 600mm and 20,000 watts respectively. To find the flow rate of prototype and velocity, height and energy dissipated in the model. Given data: Scale ratio Flow rate of the model (Qm) = 0.0995 cumecs = 0.995 m3/s Velocity of the prototype (Vp) = 9m/s Height of the prototype (Lp)= 600 mm Energy dissipated of the prototype (Ep) = 20,000 watts To find: (i) Discharge of prototype (Qp) (ii) Velocity of model (Vm) (iii) Height of model (Hm) (iv) Energy dissipated of model (Em) Solution: In this case, for spillway, Froude's model law is applied. Result: (i) Discharge of prototype (Qp) = 177.99 m3 / s (ii) Velocity of model (Vm) = 2.012m/s (iii) Height of model (Hm) = 30mm (iv) Energy dissipated of model (Em) = 0.559 watts Example - 37 A 0.5m height and 2m long model of spill way discharge 0.5 m3/s discharges under a head of 0.3m. If a 1:15 Scale ratio of this model determine prototype (spillway) dimensions, head and discharge of prototype. If prototype force of 3457200N, determine force on the model. Given data : Height of model (hm) = 0.5m Length of model (Lm) = 2m Discharge of model (Qm) = 0.5m3 / s Head of model (Hm) = 0.3m Scale ratio Force of prototype (Fp) = 3457200N To find: (i) Prototype dimension (a) height (hp) (b) Length (Lp) (ii) Head of prototype (Hp) (iii) Discharge of prototype (Qp) (iv) Force of model (Fm) Solution: In this case for spillway, Frounde's model law is applied here. Result: (i) Height of prototype (hp) = 7.5m (ii) Length of prototype (Lp) = 30m (iii) Head of prototype (Hp) = 4.5m (iv) Discharge of prototype (Qp) = 435.71m3 / s (v) Force of model (Fm) = 1024.35 N Example - 38 A spill way model is to be built in geometrically similar scale of 1/25 and length of 400 mm. The model is 0.6 m high and head 0.01m. Find the height and head of the prototype. If the flow over the model is 15 lit/sec, what flow per meter length of prototype. The negative pressure in the model is 100mm. What is the negative pressure is prototype? It is possible?. Given data: Scale ratio length of model (Lm) = 400 mm = 0.4 m Height of the model (hm) = 0.6m Head of the model (Hm) = 0.01m Flow rate of the model (Qm) = 15 lit/sec = 15 × 10-3 m3/s Negative pressure of model = -100 mm - 0.1 m To find: (i) Height of the prototype (hp) (ii) Head of the prototype (Hp) (iii) Flow rate of prototype/meter length of prototype (iv) Negative pressure of prototype (Pp) Solution: In this case, for spill way Frounde's model law is applied. This negative pressure is possible because the maximum possible negative pressure head is-7.5m of water. Result: (i) Height of the prototype (hp) = 15m Head of the prototype (Hp) = 0.25 (iii) Discharge of prototype / meter length (iv) Negative presure head in prototype = -2.5 m of water. Example - 39 A model in the scale 1/20 of a boat is towed in towed in water. The prototype is moving in sea water of density 1030kg/m3 at a velocity of 25 m/s. Find the corresponding velocity of the model in water and resistance due to wave in the model if the resistance in prototype due to the wave is 800N. Given data: Scale ratio Density of sea water in prototype (ρp) = 1030kg/m3 Velocity of prototype (Vp) = 25 m/s Resistance on prototype (FR) p = 800 N Density of water in model (ρm) = 1000 kg/m3 To find: (i) Velocity of model (Vm) (ii) Resistance force of model (FR)m Solution: In this case considering wave resistance of boat. So Froude's model law is applied. Result: (i) Velocity of model (Vm) = 5.59 m/s Resistance of model (FR)m = 0.0965 N Example - 40 The pressure drop in an aeroplane model of size 1/40 of its prototype is 80N/cm2. The model is tested in water. Find the corresponding pressure drop in the prototype. Take density of air = 1.24kg/m3. The viscosity of water is 0.01 poise while the viscosity of air is 0.00018 poise. Given data: To find: Pressure drop (ΔP)p Solution: Since both pressure force and viscous force are involved in this case. So both Euler's and Reynolds's model laws must be applicable. (ii) By Euler's model law Em = Ep Result: Pressure drop in prototype (ΔP)p = 0.01306N/cm2 Example - 41 A 1:64 Model is constructed of an open channel in concrete which has manning's N = 0.014. Find the value of N for the model. Give data: Linear scale ratio (Lr) = 64 Value of N for Prototype (Np) = 0.014 To find: Value of N for model (Nm) Solution: By manning's formula Where m = Hydraulic mean depth in m i = Slope of the bed of the channel Manning's formula for model is Mannings formula for prototype is Dividing the equation (2) by equation (1) we get For dynamic similarity, Froude model law is used Now equation (3) becomes Result : Value of N for model (Nm) = 0.007

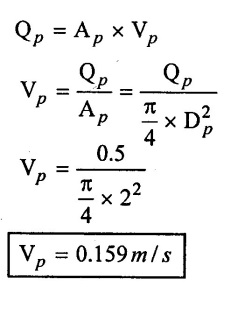

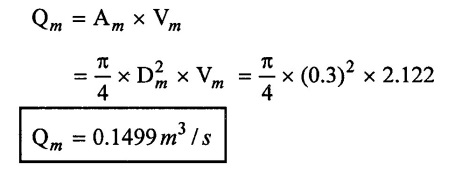



 its prototype.
its prototype.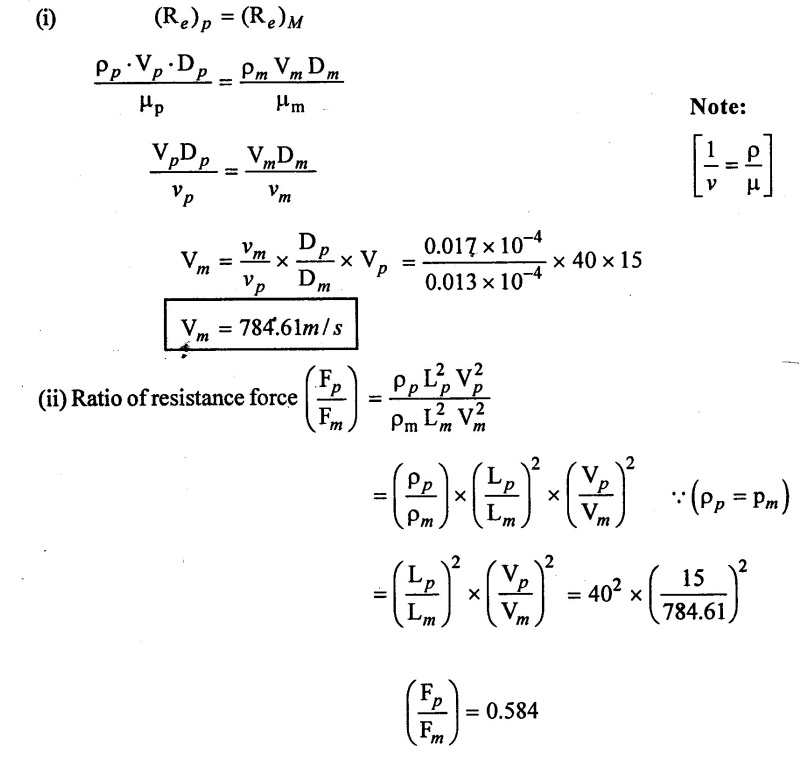
 = 0.584
= 0.584
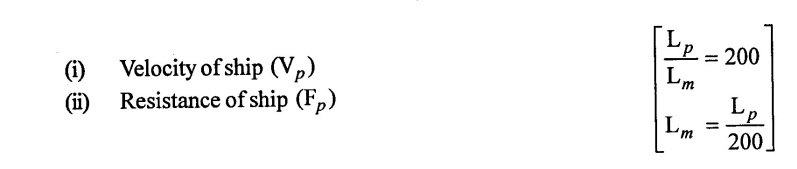
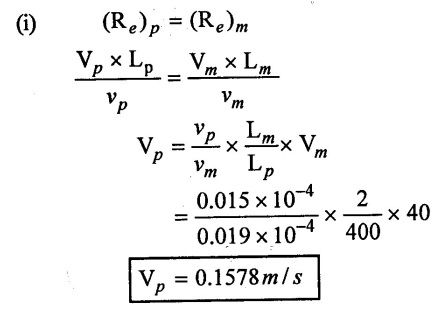








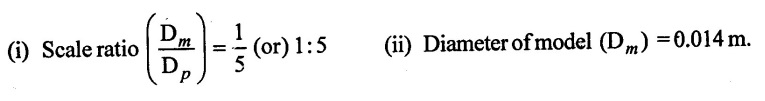
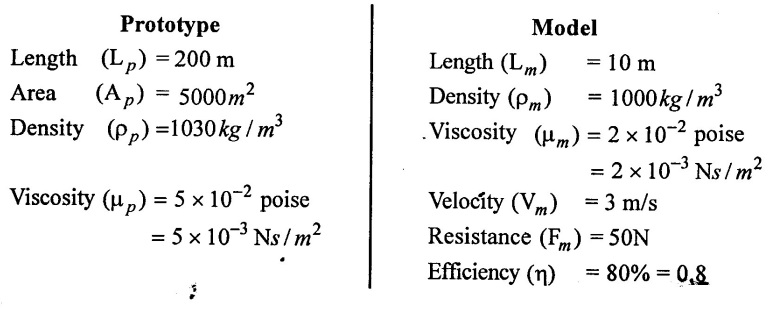

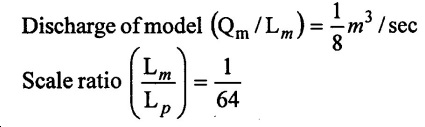
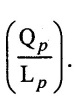
 Result:
Result: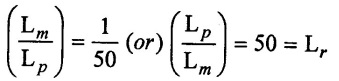
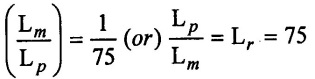

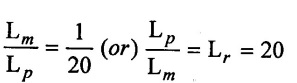
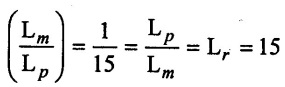
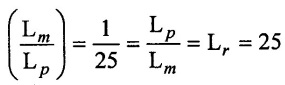
 = 4687.05 lit/sec.
= 4687.05 lit/sec.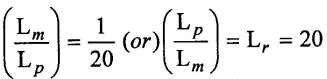


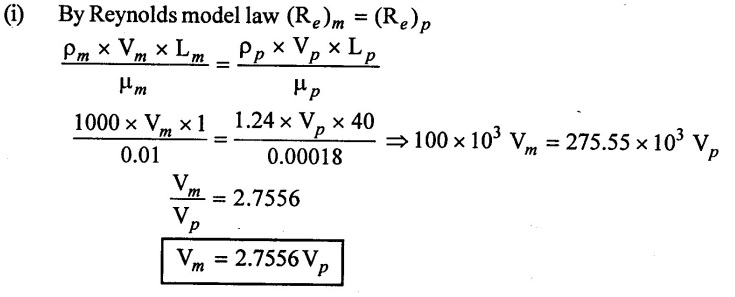

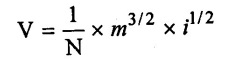
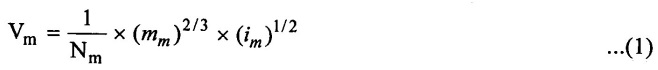

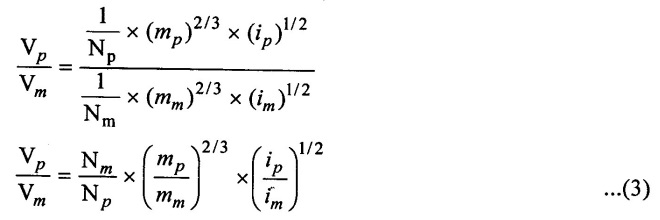


Fluid Mechanics and Machinery: Unit 3: Dimensional Analysis and Model Studies : Tag: : Fluid Mechanics - Solved Examples Based on Model Analysis
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
