Fluid Mechanics and Machinery: Unit 3: Dimensional Analysis and Model Studies
Solved Examples Based on Dimensional Analysis
Fluid Mechanics
Solved Examples Based on Dimensional Analysis: Dimensional Analysis and Model Studies - Fluid Mechanics and Machinery
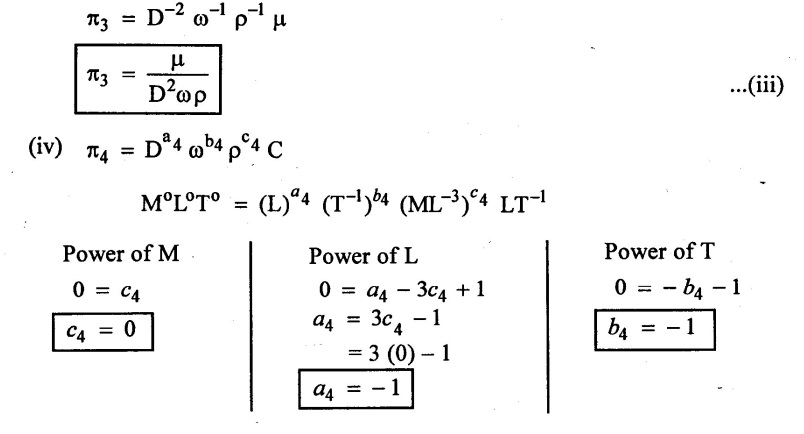
SOLVED EXAMPLES BASED ON DIMENSIONAL ANALYSIS Example - 1 Determine the dimensions of the quantities given below (i) Angular velocity (ii) Angular acceleration (iii) Discharge (iv) kinematic viscosity (v) Force (vi) specific weight (vii) Dynamic viscosity (viii) Torque (ix) power (x) momentum Given data: (i) Angular velocity (ii) Angular acceleration (iii) Discharge (iv) Kinematic viscosity (v) Force (vi) Specific weight (vii) Dynamic viscosity (viii) Torque (ix) power (x) momentum To find Dimensions of the Quantities. Solution: Result: (i) Angular velocity (ω) = T-1 (ii) Angular acceleration (α) = T-2 (iii) Discharge (Q) = L3 T-1 (iv) Force (F) = MLT-2 (v) Specific weight (w) = ML-2T-2 (vi) Torque (T) = ML2T-2 (vii) Power (P) = ML2T-3 (viii) Dynamic viscosity (μ) = ML-1T-1 (xi) Kinematic viscosity v = L2 T-1 (x) Momentum = MLT-1 Example - 2 Check the dimensional homogeneity for the equation P = w Q H Given data: P = w Q H To find: Check the dimensional homogeneity Solution: P = w Q H Dimensions of LHS = Dimensions of RHS Result: The dimensions on both sides are equal. So the given equation is dimensionally homogeneous. Example - 3 The time period (t) of a pendulum depends upon the length (l) of the pendulum and acceleration due to gravity (g). Derive an expression for the time period. Given data: Time period (t) depends upon (a) Length of pendulum (l) (b) Acceleration due to gravity (g) To find: Derive the function equation Solution: Time period (t) = seconds = T Gravity (g) = m/s2 = LT-2 Length (l) = L By using Rayleigh's Ritz method. Step - 1: Write the functional equation (based on given data) t = f (l, g) Step - 2: Write the functional equation with constant (k) and arbitary powers like as a, b, c, ...z. t = k (la, gb) …(1) Step - 3: Find the value of arbitary powers Apply MLT system in equation (1) on both sides. T1 = k [La (LT-2)b] Power of T 1 = -2b Power of L 0 = a + b a = -b Step - 4 Apply a,b values in equation (1) Result: Functional Equation is Example - 4 Find an expression for the drag force on smooth sphere of diameter D, moving with a uniform velocity V, in a fluid of density p and dynamic viscosity μ using Rayleigh's Ritz method. Given data: Drag force (F) depends on (i) Diameter (D) (ii) velocity (V) (iii) Density (ρ) (iv) Dynamic viscosity (μ) To find: Derive the functional equation Solution: Drag force (F) = N = kg·m/s2 = MLT-2 Diameter (D) = M = L Vilocity (V) = m/s = LT-1 Density (ρ) = kg/m3 = ML-3 Dynamic vescosity (μ) = N - s/m2 = ML-1T-1 Step - 1 Write the functional equation based on given F = f (D, V, ρ, μ) Step - 2 Write the functional equation with constant (k) and arbitary powers like as a, b, c,..z. F = k (Da, Vb, ρc‚ μd) ...(1) Step - 3 Find the values of arbitary Powers Apply MLT system in equation (1) on both sides. MLT-2 = k [La (LT-1)b (ML-3)c (ML-1T-1)d Power of M 1 = c + d ...(2) Power of L 1 = a + b -3 c – d ...(3) Power of T -2 = -b – d ...(4) There are four unknows (a, b, c & d) from the above equations. So express the three unknows interms of the other one unknowns which is important property like dynamic viscosity, hence expressing a, b, and c interms of d. From equation (2) 1 = c + d From equation (4) -2 = - b - d Apply the values of b and c in equation - (3) 1 = a + b − 3c – d a = 1b + 3c + d = 1 − (2 − d) + 3 (1 − d) + d = 1 – 2 + d + 3 - 3 d + d = 4 - 2 + 2d - 3d Step - 4 Apply a, b, c values in equation - (1) Result: Functional Equation Example - 5 Find the expression for the power (P) developed a pump when P depends upon the head (H), discarge (Q) and specific weight (w) of the fluid, using Rayleigh's method. Given dada: Power (P) depends on Head (H) Discharge (Q) Specific weight (w) To find: Derive the functional equation Solution: Power (P) = ML2 T-3 Head (H) = L Discharge (Q) = L3T-1 Specific weight (w) = ML-2T-2 Step - 1 Write the functional equation based on given P = f (H, Q, w) Step - 2 Write the functional equation with constant (k) and arbitary powers like as a, b, c,..z P = k (Ha, Qb, wc) ….(1) Step - 3 Find the value of arbitary powers Apply MLT system in equation (1) on both sides. ML2T-3 = k [(La) (L3T-1)b (ML-2T-2)c] Power of M 1 = c Power of L 2 = a + 3b - 2c ….(2) Power of T -3 = -b - 2c b = -2c + 3 b = -2 × (1) + 3 b = -2 + 3 b = 1 Apply the values of b & c in equation (2) 2 = a + 3b - 2c 2 = a + 3(1) − 2(1) 2 = a + 3 - 2 2 = a + 1 a = 2 - 1 a = 1 Step - 4 Apply the values of a, b, & c, in equation - (1) P = k (H1‚Q1‚w1) P = k H Q w Result:- Functional equation P = k H Q w. Example - 6 The efficiency (77) of a fan depends on the density (ρ) Dynamic viscosity(μ), angular velocity(ω), Diameter(D), and discharge (Q). Express (η) interms of dimensionless parameters using Rayleigh Ritz method. Given dada: Efficiency (η) depends on (i) Density (ρ) (ii) Dynamic viscosity(μ) (iii) Angular velocity(ω) (iv) Diameter(D) (v) Discharge (Q). Solution: Efficiency (η) = M°L°T° Density (ρ) = ML-3 Dynamic viscosity (μ) = ML-1T-1 Diameter (D) = L Angular velocity (ω) = T-1 Discharge (Q) = L3T-1 Step - 1 Write the functional equation based on given η = ƒ(ρ, μ, ω, D, Q) Step - 2 Write the functional equation with constant and arbitary powers a, b, c,..z η = k [ρa, μb, ωc, Dd, Qe] ...(1) Step - 3 Find the values of arbitary powers Apply MLT system in equation (1) on both sides. M°L°T° = k [(ML-3)a (ML-1T-1)b (T-1)c (L)d (L3T-1)e] Power of M 0 = a + b ...(2) Power of L 0 = -3a - b + d + 3e ...(3) Power of T 0 = -b – c – e ...(4) There are five unknows from the above equations. So Express the three unknowns interms of the other two unknows which are important viscosity and discharge are more important in this problem. Hence expressing a, c and d in terms of b and e. From equation (2) 0 = a + b a = - b From equation (3) 0 = -3a - b + d + 3e d = 3a + b - 3e d = 3(-b) + b - 3e d = -3b + b - 3e d = - 2b - 3e From equation - (4) 0 = -b – c - e c = -b - e Step - 4 a, c and d values are apply equation (1) Result: Functional Equation Example – 7 The pressure drop AP in a pipe diameter (D) and length (l) depends on the density (ρ) and viscosity (μ) of flowing mean velocity (V) of flow and average height of protuderance (t). Show that pressure drop can be expressed in the form Given data: Pressure drop ΔP depends on (i) Diameter (D), (ii) Length (L) (iii) Density (ρ) (iv) viscosity(μ) (v) velocity(V) (vi) Height (t) To find: Solution: Pressure drop ΔP = ML-1T-2 Diameter (D) = L Length (l) = L Density (ρ) = ML-3 viscosity (μ) = ML-1T-1 velocity(V) = LT-1 Height (t) = L Step - 1 ΔP = f (D,l,ρ,μ,V,t) Step - 2 ΔP = k [DalbρcμdVetf] ...(1) Step - 3 Apply MLT system in equation – (1) on both sides ML-1T-2 = k [La, Lb, (ML-3), (ML-1T-1), (LT-1)e, Lf] Power of M 1 = c + d; ...(2) Power of L -1 = a + b -3c - d + e + f ...(3) Power of T -2 = -d – e ...(4) There are six unknowns from the above equations. So express the three unknowns interms of the other three are more important in this problem. Hence expressing a, c, e in terms of b, d, & f, From equation - (2) 1 = c + d c = 1 - d From equation - (4) -2 = - d - e e = 2 - d From equation - (3) -1 = a + b - 3c - d + e + f Apply the values of c & e in equation – (3) we get Step - 4 Apply the values of a, c, & e in equation – (1) Result: Functional Equation Example - 8 The Resistance force R of a supersonic plane during flight can be considered as dependant upon the length of the aircraft (l), velocity (V), air viscosity (μ), air density (ρ), and bulk modulus of air (k). Express the functional relationship between these variables and the resistance force using Rayleigh's Ritz method. Given data: The Resistance force (R) depends upon (i) Length (l) (ii) velocity (V) (iii) viscosity (ρ) (iv) Density (ρ) (v) Bulk modulus (k). To find: Derive the functional equation Solution: Resistance force (R) = MLT-2 velocity (V) = LT-1 Length (l) = L viscosity (μ) = ML-1T-1 Density (ρ) = ML-3 Bulk modulus (k) = ML-1T-2 Step - 1 R = f [l, V, μ, ρ, k] R = K [la, Vb, μc, ρd, ke] Step - 3 Apply MLT system in equation (1) There are five unknowns from the above equations. So expressing the three unknowns in terms of two unknowns important property. So express the value of a,b and d in terms of c and e. From equation - (2) 1 = c + d + e From equation - (4) -2 – b - c - 2e From equation - (3) apply the values of b & d in equation -- (5) Step - 4 apply values of a, b, and d in equation - (1) Result: Functional Equation is Example - 9 A partially sub - merged body is towed in water. The resistance R to its motion depends on the density (ρ), the viscosity (μ) of water, length (l) of the body, velocity(V), of the body and the acceleration due to gravity (g). Show that the resistance to the motion can be expressed in the form of Given data: Resistance force (R) depends on, (i) Density (ρ) (ii) Viscosity (μ) (iii) length (l) (iv) velocity (V) (v) acceleration (g). To find: Show R = Solution: Resistance force (R) = MLT-2 Density (ρ) = ML-3 Viscosity (μ) = ML-1T-1 length (l) = L velocity (V) = LT-1 acceleration (g) = LT-2 Step - 1: R = ƒ(ρ, μ, l, V, g) Step - 2 Step - 3 Apply MLT system in equation - (1) There are five unknowns from the above equations. So expressing the three unknowns interms of two unknowns which are important property of this problem. Hence viscosity and gravity are important property. So express a, c and d interms of b and e. From equation - (2) 1 = a + b a = 1- b From equation - (4) - 2 = -b – d - 2e d = 2 - b - 2e From equation - (3) c = 1 + 3a + b – d – e ...(5) Apply the values of a & d in equation (5) Step - 4 Apply the values of a, c and d in equation - (1) Result. Functional Equation Example - 10 Show by dimensional analysis, that the power (P) developed by a hydraulic turbine is given by Where ρ is mass density, N is the rotational speed, D is the diameter of runner, H is the working head g is the gravitational acceleration. Given data: Power (P) depends on (i) Density (ρ) (ii) Rotational speed (N) (iii) Diameter (D) (iv) Head (H) (v) gravitational acceleration (g). To find: Show that Solution: Assume Rayleigh's Ritz method Power (P) = ML2 T-3 Rotational speed (N) = T-1 Density(ρ) = ML-3 Diameter (D) = L Head (H) = L acceleration due to gravity (g) = LT-2 Step - 1 P = ƒ (D, N, ρ, H, g) Step – 2 Step - 3 Apply MLT system in equation - (1) Expressing the three unknown variables in terms of two unknowns which are important property of this problem. Here H & g are the important property. So express a, b & c in terms of d & e. From equation (2) c = 1 From equation – (4) b = 3 - 2e From equation - (3) a = 2 + 3c – d - e a = 2 + 3 (1) – d - e a = 5 – d - e Step - 4 Apply the values a, b & c in equation – (1) Result: Functional Equation Example - 11 The Resulting force R of a supersonic plane during flight can be considered as dependent upon the diameter of the air craft (D), velocity (V), air viscosity (μ), air density (ρ) and bulk modulus of air (k). Express the functional force, using Buckingham's π-theorem. Given data: The Resistance force R depends upon (i) diameter (D) (ii) velocity (V) (iii) viscosity (μ) (iv) Density (ρ) (v) Bulk modulus (k) To find Express the functional Relationship between variables. Solution: Resistance force (R) = MLT-2 Diameter (D) = L Velocity (V) = LT-1 Viscosity (μ) = ML-1T-1 density (ρ) = ML-3 Bulk modulus (k) = ML-1T-2 Step - 1 Write the functional Equation R = ƒ (D, V, μ, ρ, k) The functional equation is must be equal to zero. So that the above equation can be written as f1 (D, V, μ, ρ, k) = 0 Step - 2 To findout of π-terms. Total number of variables (n) = 6 Number of fundamental dimension (m) = 3 ⸫ Number of dimensionless groups (oг) л-terms = n − m = 6 - 3 Number of π-term is = 3 Hence f1 (π1, π2, π3) = 0 ...(1) Step - 3 Select Repeating variables. Each π-term contains following three repeating variables (i) Geometric property = Diameter (D) (ii) Flow property = Velocity (V) (iii) Fluid property = Density (ρ) ⸫ Repeating variables = D, V, ρ Step - 4 Write the each л-terms with arbitary powers Every π -term contains (m + 1) variables (or) three repeating variables and one non-repeating variables in the sequence of given based. Repeating variables write with arbitary powers. Example a1 b1 c1 a2 b2 c2.... etc. The first л-term is non-repeating variable should be selected as dependent variable. Hence the dependent variable is Resistance force (R) and other all variables are independent variables. Step – 5 Find out arbitary powers value of Each π -terms using dimensional homogeneity Apply the values of b2 & c2 in equation – (3) Power of T 0 = - b3 - 2 b3 = - 2 Apply the values of b3 & c3 in equation (4) Step – 6 All the π-terms values are (equation i, ii, & iii) substitute in equation - (1) Step - 7 The required expression can be obtained by expressing any one of the π-terms as a function of others with constant (ϕ) Result. Functional Equation Example - 12 The efficiency (η) of a fan depends on density (ρ), viscosity (μ), speed (N), Diameter (D) of the rotor and discharge (Q). Express the efficiency (n) in terms of dimension less parameter using Buckingham's л-theorem. Given data: The efficiency (η) depends on (i) Density (ρ) (ii) viscosity (μ) (iii) speed (N) (iv) Diameter (D) (v) Discharge (Q). To find: Express the functional relationship between variables. Solution: π = M°L°T° Density (ρ) = ML-3 viscosity (μ) = ML-1T-1 speed (N) = T-1 Diameter (D) = L Discharge (Q) = L3 T-1 Efficiency (η) = M°L°T° Step - 1 Write the functional equation η = ƒ (ρ, μ, N, D, Q) Also written as, f1 (η, ρ, μ, N, D, Q) = 0 Step - 2 Find out the Number of π-terms Total Number of variables (n) = 6 Fundamental dimensions (m) = 3 Number of π-terms = n – m = 6 - 3 Number of π-terms is 3 Hence, f1 (π1, π2, π3) = 0 Step - 3 Select Repeating variables Geometric property = Diameter (D) Flow Property = Speed (N) Fluid property = Density (ρ) ⸫ Repeating variables = D, N, ρ Step - 4 Write the each π-terms with arbitary powers. Step - 5 Find out the arbitary values of each π-terms using dimensional homogeneity. Apply the values of a2, b2 & c2 in π2 terms. Step - 6 Apply the values of π1, π2 & π3 îз in equation (1) Step - 7 Expressing any one of the π-terms as a functions of others with constant ϕ Result. Functional Equation Example - 13 Show that the velocity through a nozzle jet is given by Given data: Velocity (V) is depends on the (i) Head (H) (ii) Diameter (D) (iii) viscosity (μ) (iv) Density (ρ) (v) Acceleration due to gravity (g) To find: Derive functional equation Solution: π = M°L°T° Head (H) = L Diameter (D) = L viscosity (μ) = ML-1T-1 Density (ρ) = ML-3 gravity (g) = LT-2 Velocity (V) = LT-1 Step 1 Write the functional Equation V = f (H, D, μ, ρ, g) Also can be written as f1 (V, H, D, μ, ρ, g) = 0 Step - 2 Find out the number of π-terms. Total number of variables (n) = 6 Fundamental dimensions (m) = 3 Number of л-terms = (nm) = 6 - 3 = 3 Hence f1 (π1, π2, π3) = 0 ...(1) Step - 3 Select Repeating variables. Geometric property is Head (H) Flow property is gravity (g) Fluid property is density (ρ) ⸫ Repeating variables = H, g, ρ • Fluid Mechanics and Machinery • Step - 4 Write each π-terms with arbitary powers. Step – 5 Findout arbitary power values for each π-terms using dimensional homogeneity. Apply the values of a2, b2 & c2 in π2-terms. Apply the values of a3, b3 & c3 in π3-terms. Step - 6 Apply the yalues of π1, π2 & π3 in equation - (1) f1 (π1, π2, π3) = 0 Step - 7 Expressing any one of the π-terms as a functions others with constant (ϕ) Result Functional Equation Example - 14 The pressure difference ΔP in a pipe of diameter (D) and length (l) due to turbulent flow depends on the velocity (V), Viscosity (μ), density (ρ) and roughness (k). using Buckingham's π-theorem express ΔP. Given data: Pressure difference ΔP depends on (i) diameter (D) (ii) length (l) (iii) velocity (V) (iv) viscosity (μ) (v) Density (ρ) (vi) Roughness (k). To find: Expressing the functional equation (ΔP) Solution: Pressure difference ΔP = ML-1T-2 diameter (D) = L velocity (V) = LT-1 length (l) = L viscosity (μ) = ML-1T-1 Density (ρ) = ML-3 Roughness (k) = L Step 1 Write the functional Equation ΔP = f (D, l, V, μ, ρ, k) Also can be written as f1 (ΔP, D, l, V, μ, ρ, k) = 0 Step - 2 To find the number of π-terms Total number of variables (n) = 7 Fundamental dimensions (m) = 3 number of π-terms = (n - m) = 7 – 3 = 4 Hence, f1 (π1, π2, π3, π4) = 0 ...(1). Step - 3 Select the Repeating variables Geometric property = length (l) Flow property = velocity (V) Fluid property = Density (ρ) Repeating variables = l, V, ρ Step - 4 Write the each π-terms with arbitary powers. Step - 5 To find each π-terms arbitary values by using dimensional homogeneity Apply the values of a4, b4 & c4 in π-terms. Step - 6 Apply the values of π1, π2 & π3 in π4 in equation - (1) f1 (π1, π2, π3, π4) = 0 Step - 7 Expressing any one of the π-terms as a functions of others with constant (ϕ) Result: Example - 15 The functional Torque (T) of a disc of diameter (D), rotating at a speed (N) in fluid of viscosity (μ), and density (ρ) in a turbulent flow is given by Given data: To find: Show that Solution: Torque (T) = ML2 T-2 Diameter (D) = L Rotational speed (N) = T-1 Density (ρ) = ML-3 Viscosity (μ) = ML-1T-1 Step 1 Write the functional Equation T = ƒ (D, N, μ, ρ) Also can be written as f1 = (T, D, N, μ, ρ) = 0 Step - 2 To findout number of л-terms Total number of variables (n) = 5 Fundamental dimensions (m) = 3 Number of л-terms = n – m = 5 = 2 Hence f1 (π1, π2) = 0. ….(1) Step 3 Select the repeating variables. Geometric property = Diameter (D) Flow property = Rotational speed (N) Fluid property = Density (ρ) ⸫ Repeating variables = D, N, ρ Step - 4 Write each л-terms with arbitary values. Step - 5 Find out arbitary values of each π-terms using dimensional homogeneity Apply the values of a1, b1 & c1 in л1-terms Step - 6 Apply the value of л-terms in equation - (1) Step - 7 Expressing any one of the π-terms as a function others with constant (ϕ) Result: Functional Equation Example - 16 Derive on the basis of dimensional analysis suitable parameters to present the thrust developed by a propeller. Assume that the thrust (P) depends upon the angular velocity (ω), speed of advance (V), Diameter (D), dynamic viscosity (μ), mass density (ρ), elasticity of the fluid medium which can be denoted by the speed of sound in the medium (C). Given data: Thrust (P) is depends upon the (i) Angular velocity (ω) (ii) speed (V) (iii) Diameter (D) (iv) Dynamic viscosity (μ) (v) mass density (ρ) (vi) Speed of sound (C) To find: Expressing the functional relationships between the variables. Solution: Thrust (or) Force (P) = MLT-2 Angular velocity (ω) = T-1 Velocity (or) Speed (V) = LT-1 Diameter (D) = L Dynamic viscosity (μ) = ML-1T-1 Mass density (ρ) = ML-3 Speed of sound (C) = LT-1 Step - 1 Write the functional Equation P = f (ω, V, D, μ, ρ, C) Also can be written as. f1 (P, ω, V, D, μ, ρ, C) = 0 Step - 2 Find the number of л-terms. Total number of variables (n) = 7 Fundamental dimensions (m) = 3 Number of л-terms = (n − m) = 7 − 3 = 4 Hence f1 (π1, π2, π3, π4) = 0 ….(1) Step - 3 Geometric property = Diameter (D) Flow property Angular velocity (ω) Fluid property = Density (ρ) Step – 4 write the each π-terms with arbitary powers. Step - 5 Find out arbitary values for each л-terms using dimensional homogeneity. Apply the values of a1, b1 & c1 in π1-terms. Apply the values of a2, b2 & c2 in π2 - terms Apply the values of a3, b3 & c3 in π3 - terms Apply the values of a4, b4 & c4 in π4 terms. Step - 6 Apply the values of л-terms in equation – (1) Step - 7 Expressing any oкe of л-term as a function of others with constant (ϕ) Result: Functional Equation Example - 17 Using Buckingham's π-theorem show that the discharge (Q) constant by an oil is given by Where, d is the Internal diameter of the ring, N is the rotational speed. ρ is density, μ is viscosity. σ is surface tension and w is the specific weight of oil. Given data. To find: Solution: Discharge (Q) = L3T-1 Diameter (d) = L Rotational speed (N) = T-1 Density (ρ) = ML-3 viscosity (μ) = ML-1T-1 Surface Tension (σ) = MT-2 Specific weight (w) = ML-2T-2 Step-1 Write the functional equation Q = ƒ (d, N‚ μ‚ μ‚ σ, w) Also can be written as f1 (Q, d, N, ρ, μ‚ σ, w) = 0 Step – 2 Find the number of π-terms Total number of variables (n) = 7 Fundamental dimensions (m) = 3 Number of л-terms = (n - m) = 7 – 3 = 4 Hence f1 (π1, π2, π3, π4) = 0 Step - 3 Select the Repeating variables. Geometric property = Diameter (d) Flow property = Rotational speed (N) Fluid property = Density (ρ) ⸫ Repeating variables d, N, ρ Step - 4 Write the each π-terms with arbitary powers Step - 5 Find out the arbitary values of each π-terms using dimensional homogeneity Step - 6 Apply the π-terms values in equation - (1) f1 (π1, π2, π3, π4) = 0 Step - 7 Expressing anyone of the π-term as a functions of others with constant (ϕ) Result: Functional equation Q = Example - 18. The Resulting force (F) of a subsonic plane during flight can be considered as dependant upon the length of air craft (l), velocity (V), air viscosity(μ), air density (ρ), and compressibility (C). Express the functional relationship between these variables and the resulting force using Buckingham's π-theorem. Given data: Resulting force (F) depends on the Length (l) Velocity (V) air viscosity (μ) air density (ρ) Compressibility (C) To find: Expressing the functional equation. Solution: Resulting force (F) = MLT-2 Length (l)= L Velocity (V) = LT-1 viscosity (μ) = ML-1T-1 density (ρ) = ML-3 Compressibility (C) = M-1LT2 Step - 1 Write the functional equation. F = ƒ (l, V, μ, ρ, σ, C) Also can be written as f1 (F, l, V, μ, ρ, σ, C) = 0 Step - 2 Find the number of л-terms. Total number of variables (n) = 6 Fundamental dimensions (m) = 3 Number of π-terms = (n - m) = 6 - 3 = 3 Hence f1 (π1, π2, π3) = 0 …(1) Step – 3 Select the repeating variables. Geometric property = length (l) Flow property = Velocity (V) Fluid property = Viscosity (μ) Repeating variables = l, V, μ Step – 4 Write the all the π-terms with arbitary powers Step - 5 Findout the arbitary values of each π-terms using dimensional homogeneity. Apply the values of а1‚ b1 & c1 in π1 terms Apply the values of a2, b2 & c2 in π2 - terms. Apply the values of a3, b3 & c3 in π3 - tеrms. Step - 6 Apply the π-terms values in equation (1) f1 (π1, π2, π3) = 0 Step - 7 Expressing any onе л-term value as a functions of other π -terms value with constant (ϕ) Result: Functional Equation F = Example - 19 Capillary rise (h) depends on density (ρ), acceleration (g), surface tension (σ) and radiuș of the tube (r). Show by using the Buckingham's π-theorem that Given data: Capillary rise (h) is depends on (i) density (ρ) (ii) acceleration (g) (iii) surface tension (σ) (iv) radius of tube (r). To find: Show that Solution: π = MoLoTo Capillary rise (h) = L Density (ρ) = ML-3 acceleration (g) = LT−2 surface tension (σ) = MT-2 Radius (r) = L Step - 1 Write the functional equation h = f (ρ g σ r) Also can be written as f1 (h ρ g σ r) = 0 Step - 2 Findout number of π-terms Total number of variables (n) = 5 Fundamendal dimensions (m) = 3 ⸫ Number of π-terms = (n - m) = 5 – 3 = 2 Hence f1 (π1, π2) = 0 …(1) Step - 3 Slect the repeating variables. (i) Fluid property = density (ρ) (ii) Flow property = acceleration-due to gravity (g) (iii) Geometric property = radius (r) [Note: Here the repeating variables should be re-arranged from regular procedure into given condition. The sequence of repeating variables may be rearranged such way (or) given condition.] ⸫ Repeating variables = ρ, g, r Step - 4 Write each π-terms with arbitary powers. Step - 5 Find out the arbitary power values of each π – terms using dimensional homogeneity. The values a1, b1 & c1 a is apply in π1 — terms. The values of a2, b2 & c2 is apply in π2 - terms Step - 6 Apply the values of π-terms (i.e equation (i) & ii) apply in equation - (1) Step - 7 Expressing any one of the π-terms as a functions of others with constant (ϕ) Result: Example - 20 Flow velocity (V), near a rotation disc depends on the angular velocity (ω), of the disc, radial distance (r), vertical distance (z), kinematic viscosity (v), prove that Given data: Flow velocity (V) depends on (i) angular velosity (ω) (ii) radial distance (r) (iii) vertical distance (z) (iv) kinematic viscosity (v) To find: Prove that Solution: π = M°L°T° Velocity (V) = LT-1 angular velocity (ω) = T−1 Radial distance (r) = L vertical distance (z) = L kinematic viscosity (v) = L2 T−1 Step - 1 Write the functional equation. V = f (ω, r, z, v) Also can be written as f1 (V, ω, r, z, v) = 0 Step - 2 Findout number of π-terms. Total number of variables (n) = 5 Fundamental dimensions (m) = 2 ⸫ Number of π - terms = (n - m) Note: Here M is absent only L & T occur in the given variables. So m = 2 and the repeating variables only 2 So number of π-terms = (n - m) = (5 - 2) = 3 Hence f1 (π1, π2, π3) = 0 ...(1) Step - 3 Select the repeating variables. (i) Geometry property = radial distance (r) (ii) Flow property = angular velocity (ω) So Repeating variables = r, ω Step - 4 Write the each π- terms with arbitary powers. Step - 5 Findout the arbitary power values of each π-terms using dimensional homogeneity Step - 6 The values of л – terms (i e equation (i), (ii) & (iii)) apply in equation (1) Step - 7 Expressing any one of the π-term as a functions others with constant (ϕ) Result: Example - 21 The velocity of propagation of surface waves in liquids depends on gravity (g), liquid depth (h), wave length (λ), mass density (ρ), of the liquid and its surface tension (σ). Perform dimensional analysis by Buckingham's π- method. Given data: Velocity (V) depends on (i) Acceleration due to gravity (g) (ii) liquid depth (h), (iii) Wave length (λ), (iv) Mass density (ρ), (v) surface tension (σ ). To find: Functional Equation by Buckingham's π- theorem method. Solution: Velocity (V) = LT-1 gravity (g) = LT-2 liquid Depth (h) = L Wave length (λ) = L Mass density (ρ) = ML-3 Surface Tension (σ ) = MT-2 Step - 1 Write the functional equation V = ƒ (g, h, λ, ρ, σ) Also can be written as f1 (V, g, h, λ, ρ, σ) = 0 Step - 2 Find out the number of π- terms. Total number of variables (n) = 6 Fundamental dimensions (m) = 3 ⸫ Number of π - terms = n - m = 6 - 3 = 3 Hence f1 (π1, π2, π3) = 0 …(1) Step - 3 Select the repeating variables (i) Geometric property = liquid depth (h) (ii) Flow property = gravity (g) (iii) Fluid property = density (ρ) So the repeating variables are h, g, p. Step - 4 Write the cach π - terms with arbitary powers. Step - 5 Find the arbitary power values of each π - terms using dimensional homogeneity Step - 6 The values of terms (i.e equation i, ii & iii) apply in equation (1) Step - 7 Expressing any one of the л-term as a function of others with constant (ϕ) Result Functional equation is ་ Example - 22 The discharge (Q) of a centrifugal pump depends upon the density of fluid (ρ), speed of the pump (N), diameter of the impeller (D), the manometric head (Hm) and the viscosity of fluid (μ). Show that Given data: Discharge Q is a function of (i) Density of fluid (ρ) (ii) Speed of pump (N) (iii) Diameter of impeller (d) (iv) manometric head (Hm) (v) viscosity of fluid (μ) To find: Show that Q = Solution: Discharge (Q) = L3T¬1 Density (ρ) = ML+ Speed (N) = T-1 Diameter (D) = L Mano metric head (Hm) = L Viscosity (μ) = ML-1T-1 Step - 1 Write the functional equation Q = ƒ (ρ, N, D, Hm‚ μ) Functional Equation is must be equal to zero. So above equation can be written as f1 (Q, ρ, N, D, Hm, μ) = 0 Step - 2 Find out number of π - terms Total number of variables (n) = 6 Fundamental dimensions (m) = 3 ⸫ Number of π-terms = n - m = 6 - 3 = 3 Hence f1 (π1, π2, π3) = 0 …(1) Step - 3 Select repeating variables. Geometric property = Diameter (D) Flow property = Speed (N) Fluid property = viscosity (μ) So the repeating variables are D, N, μ Step - 4 Write the each π- terms with arbitary powers. Step - 5 Findout the arbitary power values of each π - terms using dimensional homogeneity. Step - 6 Apply the values of π - terms (i.e equation i, ii, iii) in equation – (1) Step-7 Expressing any one of the л-terms as a function of othwers with constant (ϕ) Result:

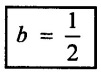


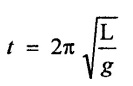
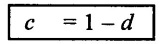


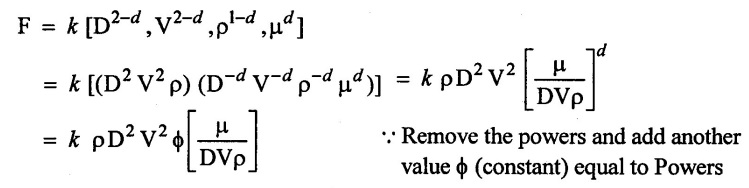

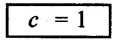
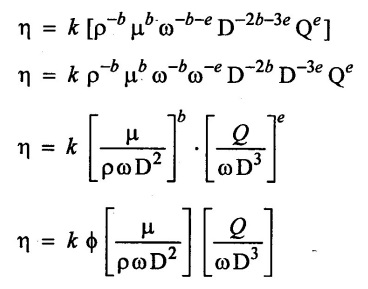
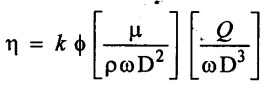
 using Rayleigh's Ritz method.
using Rayleigh's Ritz method.

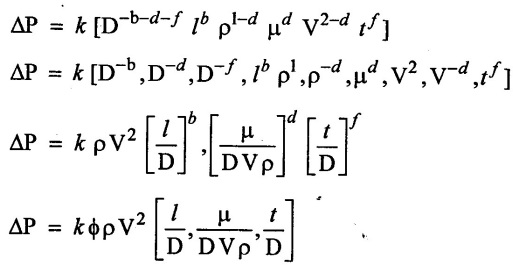


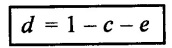



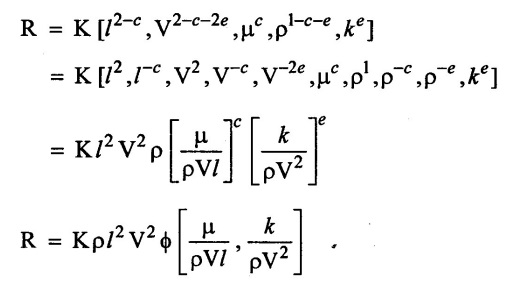
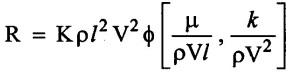




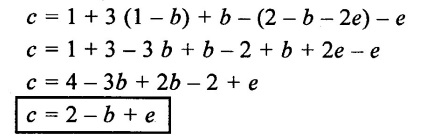





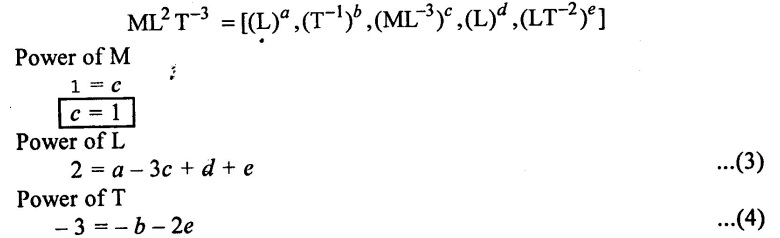
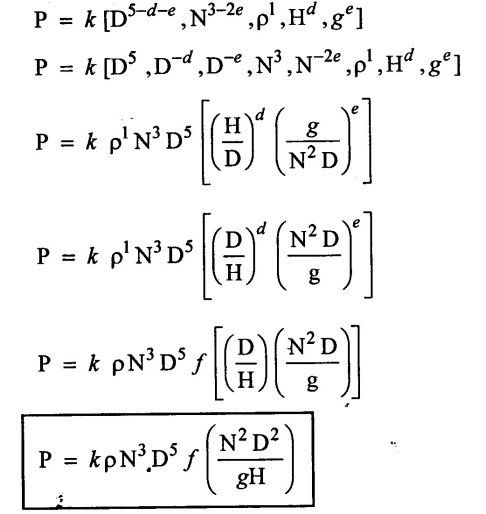
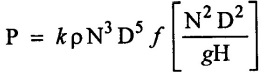


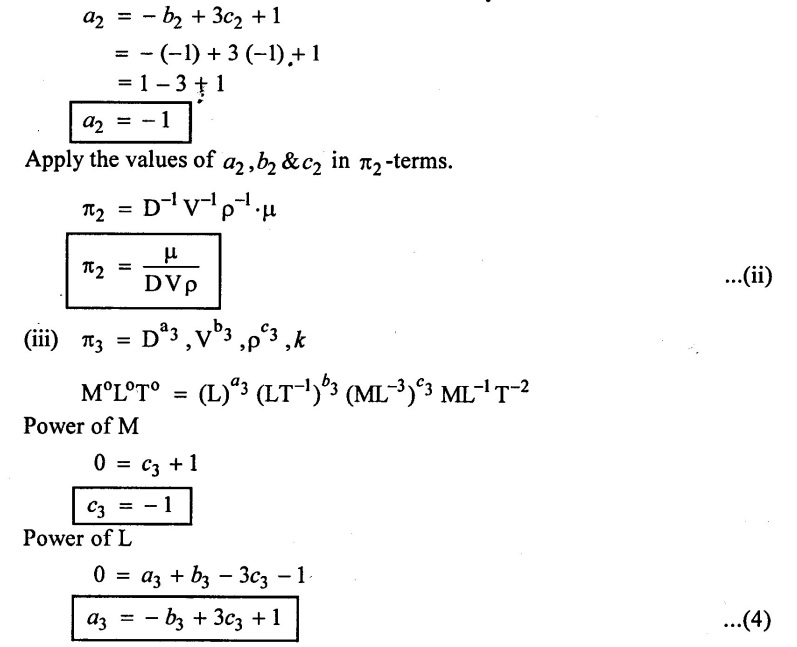
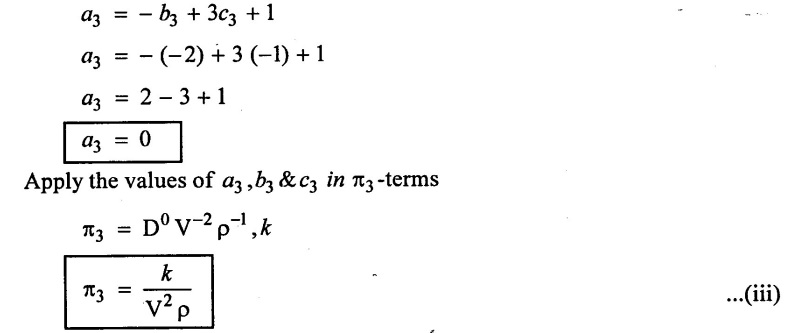



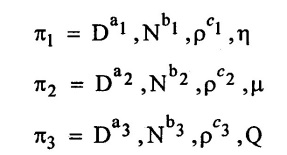


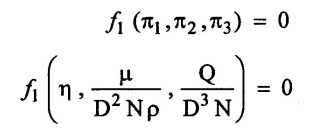


 where H is the head, D is the diameter of the jet, μ is the viscosity of co-efficient, ρ is the density of fluid and g is the acceleration due to gravity by using Buckingham's π-theorem.
where H is the head, D is the diameter of the jet, μ is the viscosity of co-efficient, ρ is the density of fluid and g is the acceleration due to gravity by using Buckingham's π-theorem.







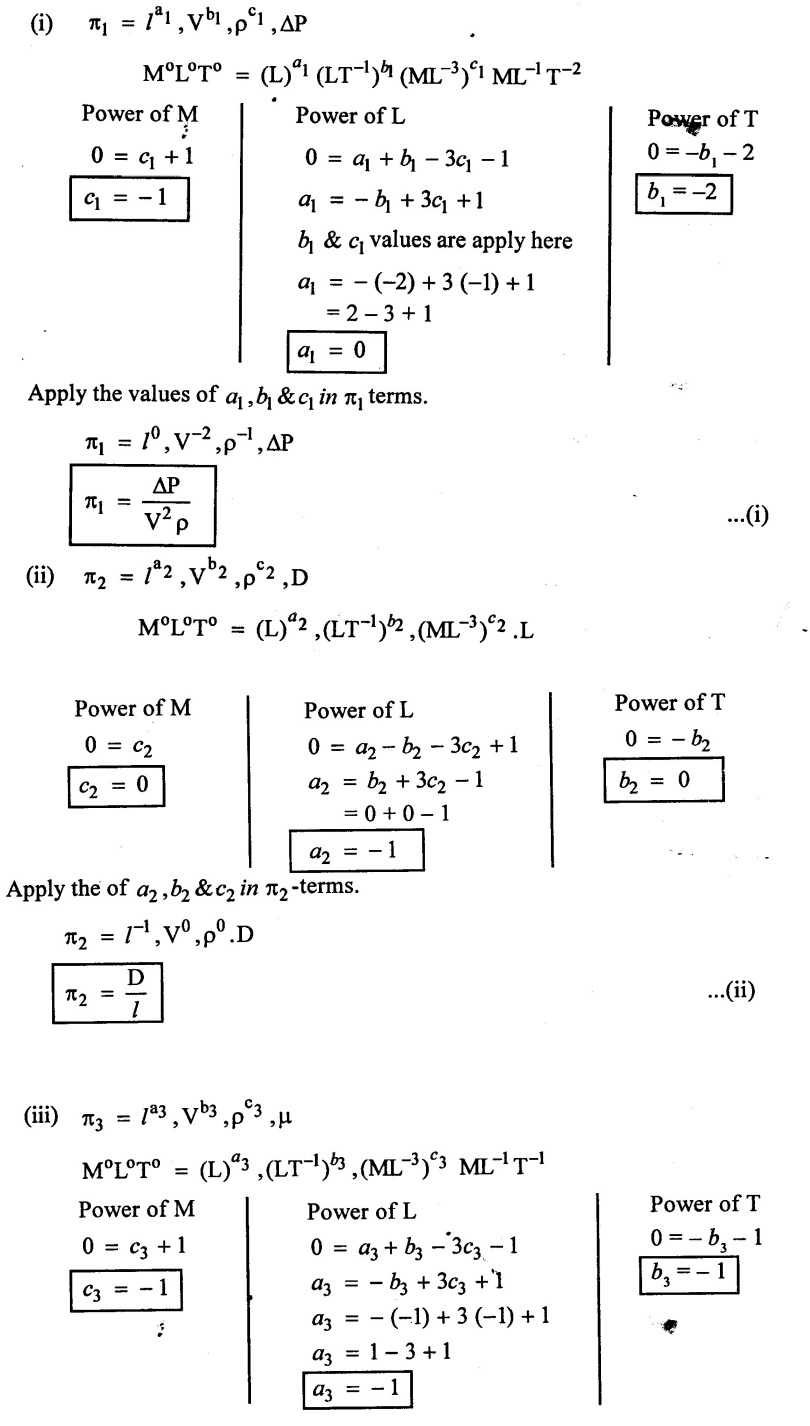 Apply the values of a3, b3 & c3 in π3-terms.
Apply the values of a3, b3 & c3 in π3-terms.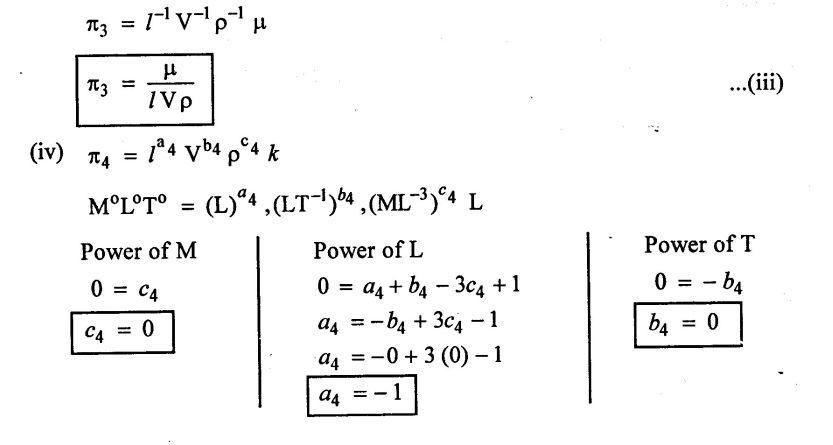



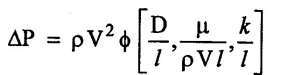



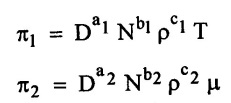





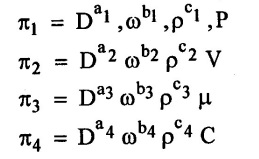


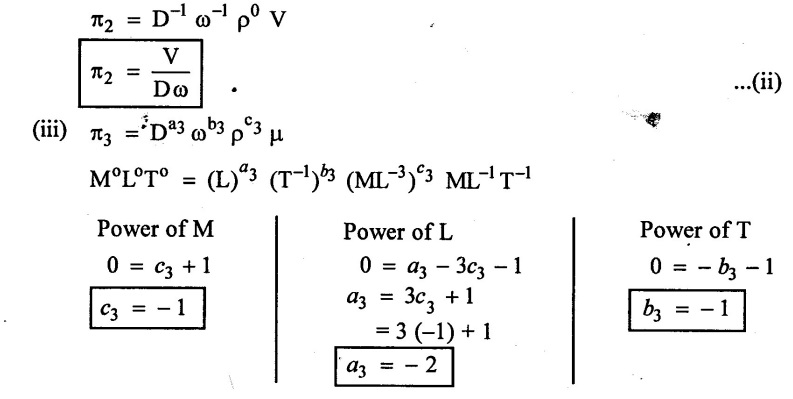


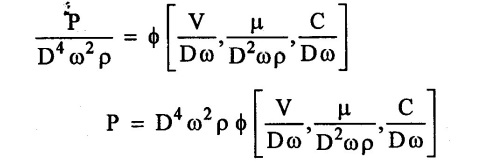




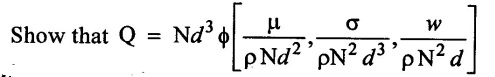


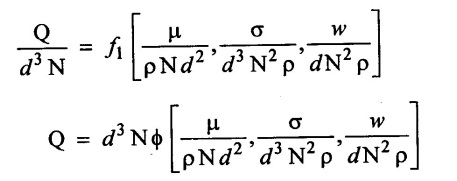
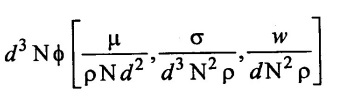



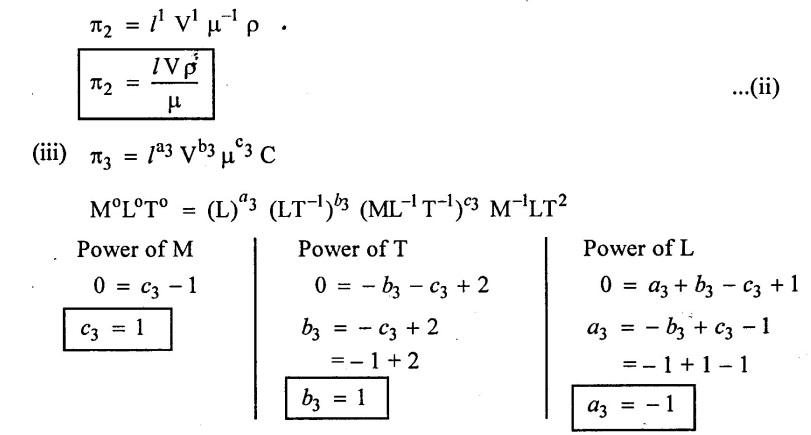










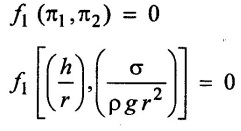



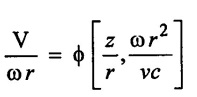
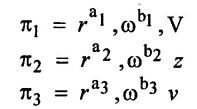


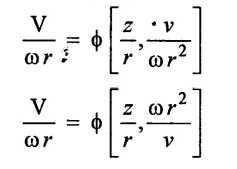




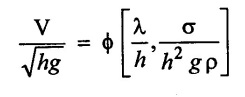
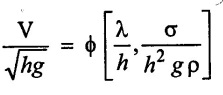
 using Buckingham's π – theorem.
using Buckingham's π – theorem.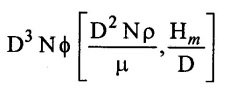


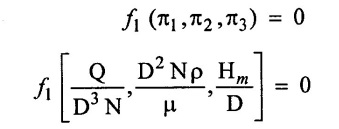


Fluid Mechanics and Machinery: Unit 3: Dimensional Analysis and Model Studies : Tag: : Fluid Mechanics - Solved Examples Based on Dimensional Analysis
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
