Fluid Mechanics and Machinery: Unit 3: Dimensional Analysis and Model Studies
Similitude
Definition, Types
Similitude is defined as the similarity between the model and its prototype.
SIMILITUDE Similitude is defined as the similarity between the model and its prototype. The results obtained from experiments on models can be applied to the prototype, when the model and prototype have similar properties (or) completely similar. Similitude is the theory and art of predicting the prototype performance from model results obtained from experiments. The theory of similitude involves the applications of dimensionless numbers. The following three types of similarities must be maintained between the model and prototype. (i) Geometric similarity (ii) Kinematics similarity (iii) Dynamic similarity. Geometric similarity refers to similarity of shape (or) form between the model and prototype. The geometrically similar systems may differ in size but they are identical in shape. In geometric similarity the model and prototype have same ratio for all corresponding linear dimensions but all included angles are some. Lm, Dm, Am, Vm and Lp, bp, Dp, Ap, Vp are the length, breadth, diameter, area and volume of a model and a prototype respectively. The figures 3.1 &3.2 are the shaper is same but size is differences and ratio of corresponding length dimensions in the model and prototype are equal. Here hp, wp, Lp and hm, wm, Lm, are the height, width and length of a model and prototype respectively. (i) For geometric similarity between model and prototype the relationship as The constant Lr is called the scale ratio (or) the scale factor. (ii) Area scale ratio (iii) Volume scale ratio In geometric similarity the area scale ratio are related by square of the scale factor and volume scale ratio are related by cube of the scale factor. Kinematic similarity means the similarity of motion between the model and prototype. The ratio of velocities and accelerations of a fluid particle at certain points in the model and at the matching point of prototype must be same in magnitude and directions. In kinematic similarity flow paths of the moving particles are same in both model prototype system. The ratio of kinematic parameters like as velocity, acceleration and discharge of the moving particles are equal. The velocity and acceleration are vector quantities, so that not only the ratio of magnitude but also the direction should be parallel. (i) Velocity scale ratio (Vr) : Let Vp1 = Velocity of fluid at point 1 in prototype Vp2 =Velocity of fluid at point 2 in prototype αp1 = Acceleration of fluid at point 1 in prototype αp2 = Acceleration of fluid at point 2 in prototype The dynamic similarity implies that the forces acting on the matching points of the prototype and its model are equal in magnitude and direction. Thus dynamic similarity is said to exist between the model and prototype. If the ratios of the corresponding forces acting at the corresponding points are equal. Also the directions of the corresponding forces at the corresponding points should be same. The forces acting on the fluid flow system are. a) Inertia force (Fi) b) Viscous force (Fv) c) Gravity force (Fg) d) Surface tension force (Fs) e) Elastic force (Fe) f) Pressure force (Fp) Let, (Fi)p - Inertia force at a point in prototype (Fv)p - Viscous force at the point in prototype (Fg)p - Gravity force at the point in prototype (Fp)p - Pressure force at the point in prototype (Fs)p - Surface tension force at the point in prototype (Fi)m, (Fv)m, (Fg)m, (Fp)m, (Fs)m corresponding values of forces, at the corresponding point in model. Fr is the force ratio In fluid mechanics, a fluid particle is subjected to a number of forces such as intertia force, viscous force, gravitational force, pressure force, surface tension force and elastic forces. The fluid flow problem the force acting on a fluid mass may be any one (or) a combination of several forces. 1. Inertia force (Fi): It is equal to the product of mass and acceleration of the flowing fluid and acts in the direction which is opposite to the direction of acceleration. It is always existing in the fluid flow problems. 2. Viscous force (Fv): It is equal to the product of shear force (τ) due to viscosity and surface area of the flow. It is present in fluid flow problems where viscosity is having an important role to play. 3. Gravity force (Fg): It is equal to the product of mass and acceleration due to gravity of the flowing fluid. It is present incase of open surface flow. 4. Pressure force (Fp): It is equal to the products of pressure intensity and cross-sectional area of the flowing fluid. It is present incase of pipe-flow. 5. Surface tension force (Fs): It is equal to the product of surface tension to length of surface of the flowing fluid. 6. Elastic force (Fe): It is equal to the product of elastic stress and area of the flowing fluid. For flowing fluid, the above mentioned forces may not always be present and also the forces, which are present in a fluid flow problem, are not equal to magnitude. These are always one or two forces which dominate the other forces.1. Geometric Similarity
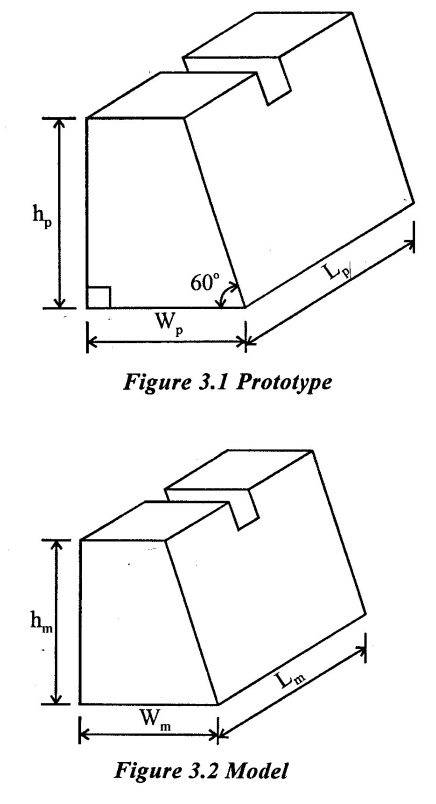



2. Kinematic Similarity


3. Dynamic Similarity


4. Types of Forces Acting in Moving Fluid.
Fluid Mechanics and Machinery: Unit 3: Dimensional Analysis and Model Studies : Tag: : Definition, Types - Similitude
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
