Materials Science: Unit I: Crystallography
Linear Density and Planar Density
with Solved Example Problems | Crystallography
Linear Density (L.D.): It is defined as number of atoms per unit length whose centres on the direction vector for specific crystallographic direction.
LINEAR DENSITY AND PLANAR DENSITY Linear Density (L.D.): It is defined as number of atoms per unit length whose centres on the direction vector for specific crystallographic direction. This is defined as the number of atoms per unit length along a specific crystal direction. i.e., Number of atoms centred on direction vector / Length of direction vector The unit of linear density is m-1, nm1) The planar density of a crystal is the density of atoms in a crystal plane. This is defined as the number of atoms per unit area on a crystal plane. This affects significantly the rate of plastic deformation. It is defined as the number of atoms per unit area. = Number of atoms in a plane / The area of the plane The unit of planar density is m-2, nm-2 Problem 1.1 What is the linear density of equivalent points in the [112] direction of copper (fcc)? Solution: Since it is fcc structure and rCu = 1.278 Å, a = 2 √2 rCu = 3.614 Å The length of the lattice vector in [112] direction = 2.26 × 109 atoms / m. Problem 1.2 Calculate the planar density of (fcc) nickel in (100) plane. The radius of nickle atom is 1.245 Å. Solution: Number of atoms in (100) plane = 1 + 1/4 × 4 = 2 Radius of atom, r = 1.245 Å But, Lattice constant, a = 4r/√2 = 2√2 r = 2√2 × 1.245 Å (⸪ fcc) = 3.52 Å Area of plane = a × a Relation between lattice constant (a) and density (ρ). Consider a cubic crystal of lattice constant a. Density of the crystal = ρ Volume of the unit cell = a3 ⸫ Mass of the unit cell = ρ a3 ...(1) [⸫ Density = Mass / Volume] Number of atoms per unit cell = n Atomic weight of the material = M Avogadro's number = N Avogadro's number is the number of atoms or molecules per kg mole of the substance Mass of each atom = M/N Mass of each unit cell = Mass of each atom in unit cell × Number of atoms per unit cell Mass of each unit cell = M/N × n …..(2) (for n atoms per unit cell) From equations (1) and (2), we have From the above expression, the lattice constant 'a' is calculated. asPlanar density (PD):
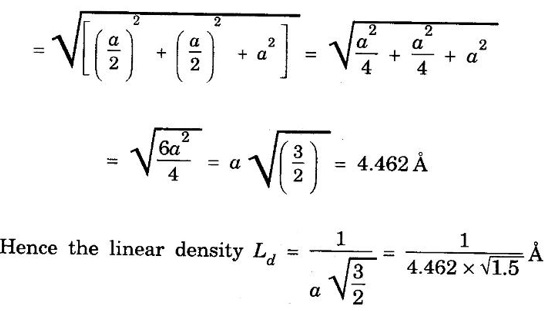


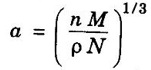
Materials Science: Unit I: Crystallography : Tag: : with Solved Example Problems | Crystallography - Linear Density and Planar Density
Related Topics
Related Subjects
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
