Materials Science: Unit I: Crystallography
Hexagonal close-packed (HCP) Structure
Atoms per unit cell, Coordination number, Atomic radius, Packing factor, Examples
In this type of crystal structure, the unit cell has one atom at each of the 12 corners of the hexagonal face, one atom each at the centre of the two hexagonal faces.
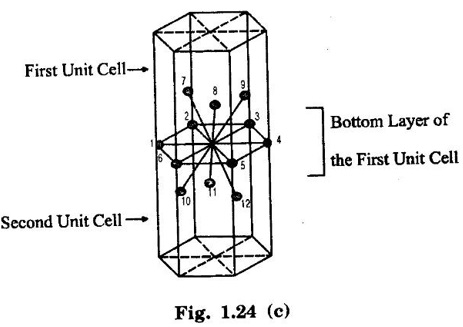
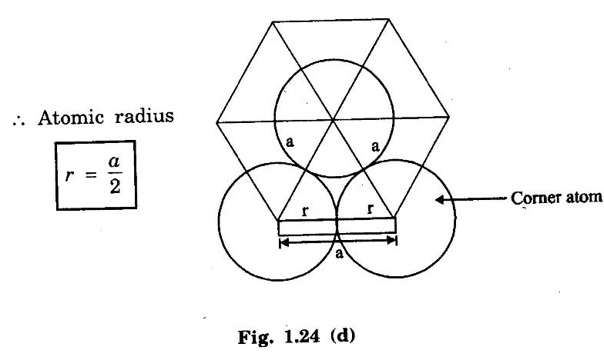
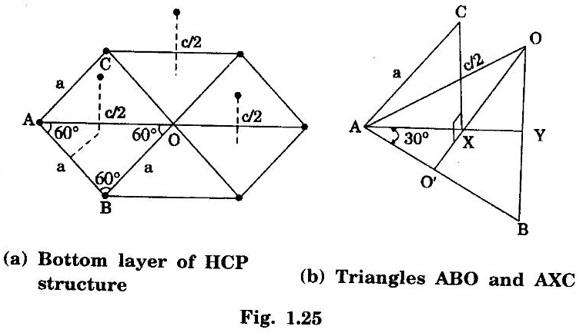
HEXAGONAL CLOSE-PACKED (HCP) STRUCTURE A unit cell of a close-packed hexagonal structure is shown in fig 1.24 (a). In this type of crystal structure, the unit cell has one atom at each of the 12 corners of the hexagonal face, one atom each at the centre of the two hexagonal faces. 3 atoms symmetrically arranged inside the unit cell. There are 3 layers of atoms in it. At the bottom layer (A), the central atom has '6' nearest neighbouring atoms in the same plane. The second layer (B) which is at a distance c/2 from the bottom layer has 3 atoms as shown in fig. 1.24 (b). The third layer ie., the layer similar to the bottom layer which is at a distance 'c' from the bottom layer. Thus, HCP structure has the stacking sequence of AB, AB ... Each corner atom is shared by 6 surrounding unit cells, i.e., each corner atom gives 1/6 th of its share to unit cell. Number of atoms due to corner atoms in upper hexagonal plane of unit cell = 1/6 × 6 = 1 Number of atoms due to corner atoms in lower hexagonal plane of unit cell = 1/6 × 6 = 1 Each central atom in the upper and lower planes (base central atom) is shared by two unit cells. It means that the upper and lower planes of the given unit cell contain 1/2 atom each. ⸫ Total number of central atoms in both upper and lower planes = 1/2 × 2 = 1 There are '3' atoms completely inside the unit cell which are not shared by any other adjacent unit cells. ⸫ Total number of atoms in a hcp unit cell = 1+1+1+3 = 6 Consider the bottom layer, the central atom has 6 nearest neighbouring atoms in the same plane. At a distance ‘c’/2 from the bottom layer, there are two layers, one above and the other below the bottom layer containing 3 atoms in each layer are also neighbouring atoms. In total, there are 12 (3 + 6 + 3) nearest neighbouring atoms. (Fig. 1.24 (c)) ⸫ Coordination number = 12 Atoms touch each other along the edges of the hexagon. Thus, from the figure 1.24 (d), the nearest neighbouring distance a = 2 r. Let 'c' be the height of the unit cell of HCP structure and 'a' be the distance between two neighbouring atoms. Consider a triangle ABO in the bottom layer of unit cell of HCP structure (fig 1.25). Here A, B and O are the lattice points and exactly above these atoms at a perpendicular distance 'c'/2, the next layer atom lies at C. Δ ABO is an equilateral triangle. A line AY is drawn ⊥r to BO (Fig. 1.25 (b)). Then, cos 30° = AY / AB X is a centre for Δ ABO Substituting for AY, we get In the ΔAXC, plane AXC is perpendicular to the plane ABO Taking square root on both sides, we have Volume of all the atoms in a unit cell (v) Number of atoms per unit cell n = 6 Atomic radius r = a/2 Volume of all 6 atoms in the unit cell v = 6 × 4/3 π r3 Substituting for r, we have Volume of the unit cell (V) Area of the base of the hexagon = 6 × Area of triangle AOB Substituting v and V, we have Therefore, packing factor is 74% ie., 74% of the volume of unit cell is occupied by the atoms and the remaining 26% volume is vacant. Note: Packing factors of FCC and HCP structures are same and they are known as closely packed structures Magnesium, zinc, titanium, zirconium, beryllium and cadmium.
1. Number of atoms per unit cell
2. Coordination number
3. Atomic radius (r)
4. Calculation of c/a ratio
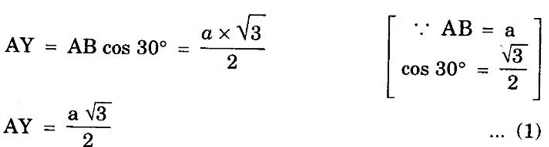

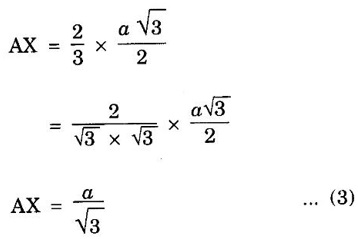


5. Packing factor



Common examples of HCP structure

Materials Science: Unit I: Crystallography : Tag: : Atoms per unit cell, Coordination number, Atomic radius, Packing factor, Examples - Hexagonal close-packed (HCP) Structure
Related Topics
Related Subjects
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
