Materials Science: Unit I: Crystallography
Face-centred Cubic (FCC) Structure
Atoms per unit cell, Coordination number, Atomic radius, Packing factor, Examples
In this type of crystal structure, the unit cell has one atom at each corner of the cube and one atom at the centre of each face. (fig. 1.20).
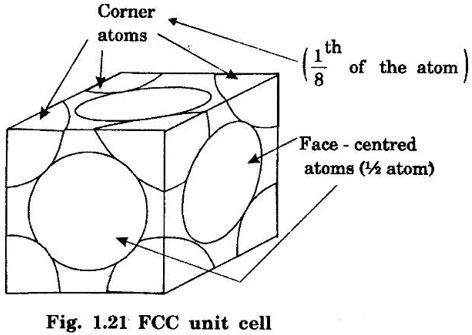
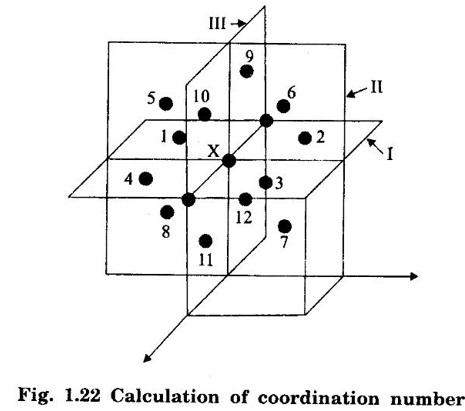
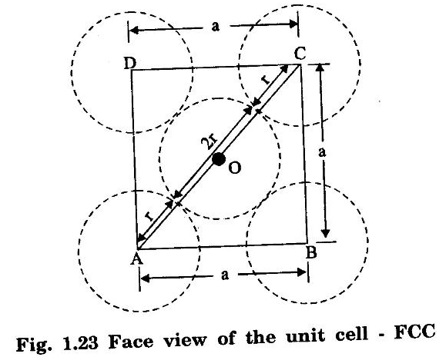
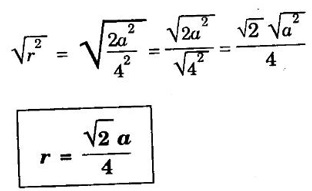
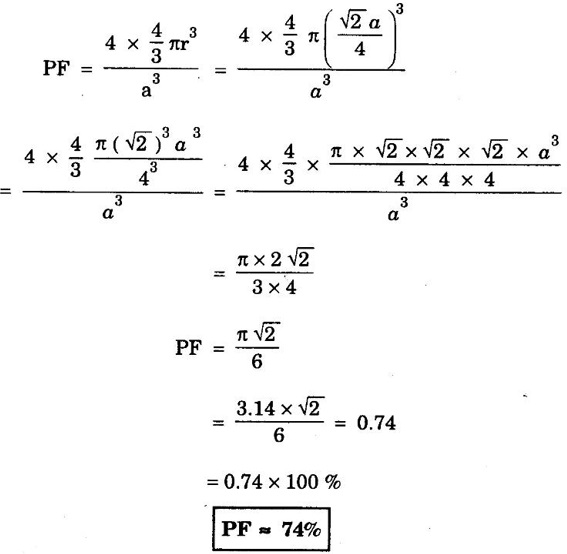
FACE-CENTRED CUBIC (FCC) STRUCTURE In this type of crystal structure, the unit cell has one atom at each corner of the cube and one atom at the centre of each face. (fig. 1.20). This structure is close-packed because each atom has 12 nearest neighbours. This type of structure is more common in metals. A unit cell of a face - centred cubic structure is shown in fig. 1.21. There are 8 corner atoms, one at each of its 8 corners. Each corner atom is shared by 8 surrounding unit cells. Share of each unit cell = 1/8 of corner atoms. Number of atoms per unit cell from the contribution of corner atoms = 1/8 × 8 = 1 atom In addition, there are 6 atoms at the 6 face centres of the cube. Each face-centred atom is shared by 2 adjascent unit cells. Hence, the share of each unit cell = ½ of face - centred atoms ⸫ Number of atoms in the unit cell from the contribution of face-centered atom = 1/2 × 6 = 3 atoms ⸫ Total number of atoms per unit cell = 1 + 3 = 4 atoms In FCC structure, there are 8 corner atoms and 6 face centred atoms one at the centre of each face of the unit cell. Consider a corner atom (X) of a unit cell as shown in fig. 1.22. There are three mutually perpendicular planes with a common point of intersection on the atom X. In plane I, it has 4 face centred atoms (1, 2, 3, 4) as nearest neighbours. In plane II, it has 4 more face centred atoms (5, 6, 7, 8) as nearest neighbours for the corner atom X. Similarly, plane III has 4 more face centred atoms, (9, 10, 11, 12) as nearest neighbours to the corner atom X. Therefore, total number of nearest atoms to any corner atom is 4 + 4 + 4 = 12 Hence, coordination number is 12. Note: The coordination number can also be found by taking face centred atom as the reference atom, nearest neighbouring atoms are corner atoms. It is found to be the 12. Consider the atoms at A and C in a face of unit cell of FCC. These atoms lie in a straight line along the face diagonal AC. The atoms touch each other along the face diagonal of the cube. The length of the face diagonal AC = r + 2r + r = 4r (Fig. 1.23). In right angled Δ ABC AC2 = AB2 + BC2 Substituting for AC2, AB2 and BC2 from fig 1.23, we have (r + 2r + r)2 = a2 + a2 [⸪ AC = 4r] (4r)2 = a2 + a2 42r2 = 2a2 Taking square root on both sides, we have Number of atoms per unit cell = 4 Side of the unit cell = a Volume of the unit cell V = a3 Packing factor =v/V Substituting for v, V and r, we have Thus, the packing factor is 74% ie., 74% of the volume of unit cell is occupied by atoms and the remaining 26% volume is vacant. Copper, aluminuim, nickel, gold, lead and platinum. Note: Packing factor of FCC = √2 × Packing factor of SC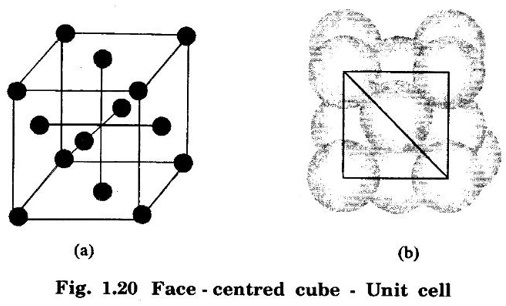
1. Number of atoms per unit cell
2. Coordination number
3. Atomic radius
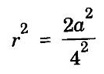
4. Packing factor
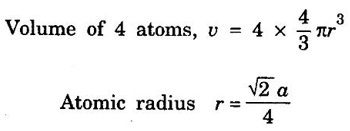
Common examples of this type of structure
Materials Science: Unit I: Crystallography : Tag: : Atoms per unit cell, Coordination number, Atomic radius, Packing factor, Examples - Face-centred Cubic (FCC) Structure
Related Topics
Related Subjects
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
