Materials Science: Unit I: Crystallography
Directions in Crystal
It is always useful to have a convention or standardized procedure to specify the directions in a crystal.
DIRECTIONS IN CRYSTAL It is always useful to have a convention or standardized procedure to specify the directions in a crystal. The procedure of finding the directions inside the crystal is explained below. 1. Consider any lattice point that lies on the line as origin. 2. Write down the position vector of the next nearest point on the line in terms of the fundamental translation vector 3. Now the components of position vector Let us apply this procedure to find the directions of OP, OQ and OR of an orthorhombic unit cell (a ≠ b ≠ c; α = β = γ = 90°) in Figure 1.26 taking 'O' as origin. Position vector of OP = ⸫ r1 = 1; r2 = 1; r3 = 1 ⸫ Direction of OP is represented by [111] Position vector of OQ = ⸫ r1 = 1; r2 = 0; r3 = 0 ⸫ Direction of OP is represented by [100] Position vector of OR = ⸫ r1 = 1; r2 = 0; r3 = 1 ⸫ Direction of OP is represented by [101] It should be understood that the directions [222], [333], [444], [n r1 n r2 n r3] will all coincide with [1 1 1]. In such cases the lowest combination of integers i.e., [1 1 1] is used to specify the direction. If any of the integers is negative, for example - 3, it should be written as 3 which is read 3 bar. Given three integers of a direction, a family of directions with different possible combinations of them, both positive and negative, is represented with brackets of the type < >. For example, a family of directions such as [132], [312], [123],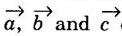 
of the unit cell of the crystal, say,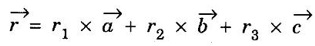 
along the three directions of a, b, c are r1, r2, r3 respectively. Then the crystal direction is denoted by [r1 r2 r3].
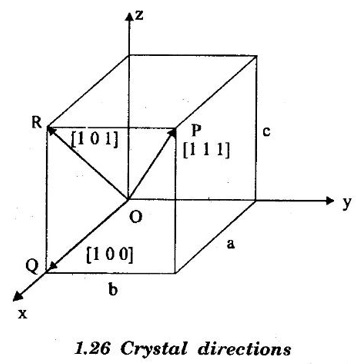
(a) Direction of OP
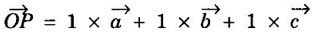
(b) Direction of OQ
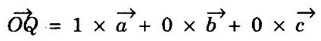
(c) Direction of OR
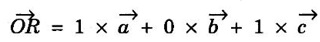
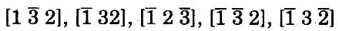etc., is represented by <132>.
Materials Science: Unit I: Crystallography : Tag: : - Directions in Crystal
Materials Science: Unit I: Crystallography
Under Subject
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation