Dimensionless Parameters in Fluid Mechanics

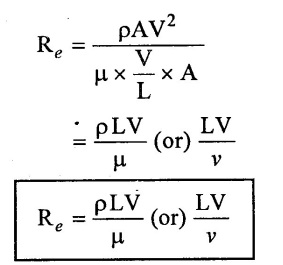
DIMENSIONLESS PARAMETERS

Dimensionless parameters are useful in fluid mechanics when any of two forces are pre-dominant. Hence dimensionless parameters are the ratio of two forces which are pre-dominant. It is a pure number and the ratio of two-quantities with the same dimensions is dimensionless. Since the inertia force is always present in a fluid flow, its ratio with each of the other forces provides a dimensionless number.

The following six dimensionless parameters

(i) Reynolds number (Re)

(ii) Froude number (Fe)

(iii) Weber number (we)

(iv) Mach number (M) (or) Cauchy number

(v) Euler number (Eu) (or) Pressure co-efficient (Cp)

(vi) Thoma (or) Cavitation number

1. Reynolds Number (Re).

It is defined as the ratio of the inertia force to the viscous force of a flowing fluid.

Hence

Where

ρ - density in kg/m3

V - velocity in m/s

L - length in m

μ - dynamic viscosity in N-s/m2

v - Kinematic viscosity in m2/s

Application:

(i) The value of Reynolds number used to find out the nature of flow, such as laminar (or) Transition (or) turbulent flow in pipes.

(ii) This number is importance when the viscous forces are of considerable magnitude in comparison with the inertia forces.

(iii) Reynolds number is used extensively for correlation in fluid machines.

(iv) It is used for study of motion of completely submerged bodies like submarines, aeroplanes and auto motives and also used for incompressible flow through pipes, bends and turbines in which inertia and viscous forces are predominant.

2. Froude's Number (Fr)

It is the square root of the ratio of inertia force to the gravitational force. Froude's number is used where inertia and gravitational forces are predominate.

Inertia force = Mass × acceleration

= Volume × density × acceleration

= ρ × A × V2     [A = L2] 

= ρ × L2 × V2

Gravitational force = Mass × gravity

= Volume × density × g

Application.

(i) Froude's number is used to indicates the resistance of partially submerged object moving through to water.

(ii) It is also used for the study of fluid flow from open hydraulic structures such as spill ways,

(iii) Inverse of the square of Fr is known as Richardson number. It is important of natural and forced convection.

3. Weber's Number (we):

It is the square root of the ratio of the Inertia force to the surface tension force in the fluid

Application:

(i) The Weber's number is used for the study of capillary movement of water in sail and flow of blood in arteries and veins when the surface tension forces are predominant in the flow.

(ii) It is also used thin sheet flows and liquid atomization.

(iii) It is useful in analyzing fluid flows where there is an interface between two different fluids especially for multiphase flows with strong curved surfaces.

4. Mach Number (M) :

Mach number is the square root of the ratio of inertia force to the elastic force in the fluid. Elastic force becomes predominant in compressible fluids. Mach's number is significant in finding dynamical similarity of the fluids where elastic force are predominant. 

Application

(i) Mach number is used for the study of flow at high speed such as flow in pipes, water hammer effect, high speed motion objects like aeroplanes, projective and missiles in atmosphere where elastic force is predominant.

(ii) It is also used check whether the fluid can be considered compressible or not. It is analogous to Froude number.

(iii) When density variation due to pressure is significant the mach number is used for modeling.

5. Euler's Number (Eu)

It is the square root of the ratio of inertia force to the pressure force in the fluid.

Application

(i) The Euler's number is used for the study of fluid where pressure force is predominant such as water hammer effects in penstocks, discharge co-efficient of orifices. Sluice gates and mouth piece.

(ii) Used in fluid flow calculations where local pressure drop in necessary and characterize the loses in the flow.

(iii) Eu = 1 Corresponds to a perfect friction less fluid flow.

6. Thoma (or) Cavitations Number (Ke)

It is the ratio between pressure difference to kinetic energy of flowing fluid. In liquid flows, vaporization begins when the pressure reduces locally to the vapor pressure of the liquid. This phenomenon is known as cavitations.

Occurrence of cavitation results in vibration, erosion of surface material, loss inefficiency and reduction in discharge.

Where

P - Local pressure

Pv - Vapour pressure

Application

The estimation of accurance and severity of cavitation in done by using the cavitation number.