Engineering Materials and Metallurgy: Unit 0: Review of Crystal Physics
Unit Cell Characteristics
Crystal Physics
A unit cell is characterised by 1. An effective number of atoms, 2. Coordination number, 3. Atomic radius, 4. Atomic packing factor, and 5. Void space and density. 1. An effective number of atoms, 2. Coordination number, 3. Atomic radius, 4. Atomic packing factor, and 5. Void space and density.
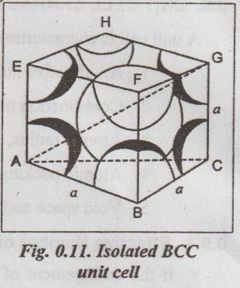
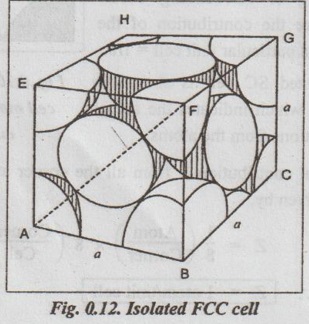
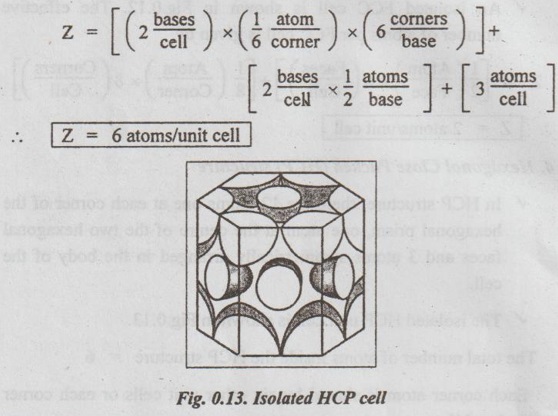
UNIT CELL CHARACTERISTICS A unit cell is characterised by 1. An effective number of atoms, 2. Coordination number, 3. Atomic radius, 4. Atomic packing factor, and 5. Void space and density. ✓ If the arrangement of atoms inside the unit cell is known, the number of atoms possessed by the unit cell can be calculated. ✓ The effective number of atoms per unit cell is equal to the product of the number of atoms per lattice point and the number of lattice points per unit cell. 1. Simple Cubic Structure ✓ In SC structure, there are 8 atoms, one at each corner of the cube and all of them are shared by 8 adjoining or surrounding cubes. Therefore the contribution of the atom to a particular unit cell = 1/8. ✓ An isolated SC cell is shown in Fig.0.10 which indicates the actual contributions from the atoms. ✓ The total contribution Z from all the corner atoms to the unit cell is given by, ✔ In BCC structure, there are 8 atoms one at each corner of the cube. They are shared by 8 surrounding cubes, plus one centre atom at the centre of the cube. ✓ An isolated BCC cell is shown in Fig.0.11 which indicates the actual contributions from the atoms. ✓ The effective number of atoms per BCC cell is given by, ✔ In FCC structure, there are 8 atoms one at each corner of the cube plus 6 face centred atoms at 6 planes of the cube. Each corner atom is shared by 8 surrounding cubes, and each face centred atoms is shared by 2 surrounding cubes. ✓ An isolated FCC cell is shown in Fig.0.12. The effective number of atoms per FCC cell is given by ✔ In HCP structure, there are 12 atoms one at each corner of the hexagonal prism, one atom at the centre of the two hexagonal faces and 3 atoms symmetrically arranged in the body of the cell. ✔The isolated HCP unit cell is shown in Fig.0.13. The total number of atoms inside the HCP structure = 6 Each corner atom is shared by six other unit cells or each corner atoms has 1/6 atom. Number of atoms in the upper hexagonal plane = 1 × 6 = 1 Number of atoms in lower hexagonal plane = 1 × 6 = 1 Each central atom is shared by two unit cells, which means upper and lower planes contain ½ atom each. ⸫ Total number of central atoms in both upper and lower planes = 1/2 × 2 = 1 and number of central atoms = 3 ⸫ The total number of atoms in HCP crystal = 1 + 1 + 1 + 3 = 6 The total contribution to the effective number of atoms in the cell can also be given by,1. Effective Number of Atoms per Unit Cell


2. Body Centred Cubic (BCC) structure
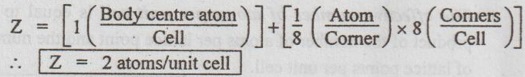
3. Face Centred Cubic (FCC) structure
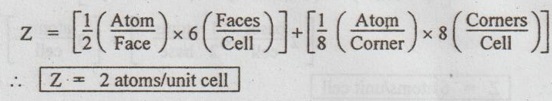
4. Hexagonal Close Packed (HCP) structure
Engineering Materials and Metallurgy: Unit 0: Review of Crystal Physics : Tag: : Crystal Physics - Unit Cell Characteristics
Related Topics
Related Subjects
Engineering Materials and Metallurgy
ME3392 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
