Basic Electrical and Electronics Engineering: Unit II: Electrical Machines
Torque and Speed Equations of DC Motors
Torque is nothing but turning or twisting force about an axis. It is measured by the product of the force and the radius at which this force acts.
TORQUE AND SPEED EQUATIONS Torque is nothing but turning or twisting force about an axis. It is measured by the product of the force and the radius at which this force acts. Consider a pulley of radius r metre acted upon by a circumferential force of F newton which causes it to rotate at speed N rpm. Torque, T = F × r (N - m) Work done by this force in one revolution = Force × distance = F × 2πr Joules and P = power developed Let Ta be the gross torque developed by the armature of motor running at N rpm. It is also called armature torque. Elelectrical power converted into mechanical power in the armature = EbIa watts ... (2) Equating (1) and (2) we get, but Eb in a motor is given by Then equation (3) becomes, This is the expression for armature torque equation of DC motor. From the above equation, it is noted that The torque which is available for doing useful work is known as shaft torque (Tsh). The gross torque Ta developed in the armature of a motor is not present at the shaft because a part of it is lost, in over coming the iron and frictional losses in the motor. Hence, Shaft torque Tsh is less than the armature torque Ta. The difference (Ta - Tsh) is known as Lost torque. The output of the motor is given by We know that the voltage equation of a motor, Eb = V - Ia Ra But, Eb in a motor is given by, Hence, speed is directly proportional to back emf Eb in the dc motor. If a de motor has initial values of N, ϕ and Eb as N1, ϕ1 and Eb1 respectively and the corresponding final values of N2, ϕ2 and Eb2, then where Ia1 = initial armature current. Ia2 = final armature current. The speed regulation of a motor is the change in the speed from full load to no load and expressed as a percentage of speed as full load (i.e.,) where No = No load speed N = full load speed Problem 2.20 Calculate the value of torque established by the armature of a 4-pole motor having 774 conductors, two paths in parallel, 24 m Wb flux per pole, when the total armature current is 50 A. Solution : Ta = 0.159 × 774 × 24 × 10-3 × 50 × (4/2) = 295.35 N-m [Ans.] Problem 2.21 A d.c. motor takes an armature current of 110 A at 480 V. The armature circuit resistance is 0.2Ω. The machine has 6 poles and the armature is lap- connected with 864 conductors. The flux per pole is 0.05 Wb. Calculate (i) the speed and (ii) the gross torque developed by the motor. Solution : = 756 N-m. [Ans.]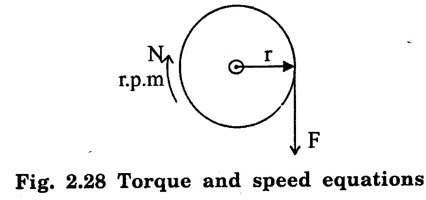

1. Armature torque of a motor
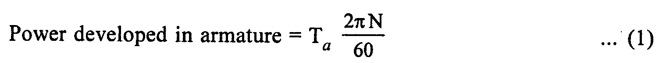
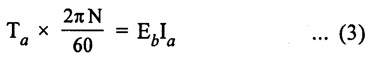
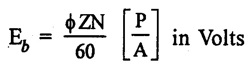
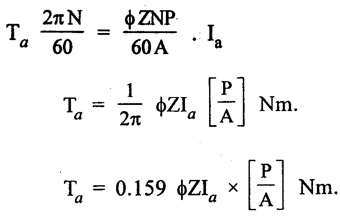
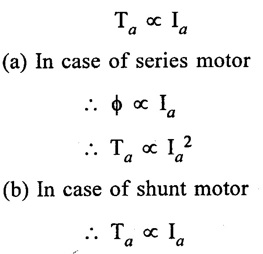
2. Shaft torque (Tsh) :

3. Speed of a DC motor (N)

4. Speed Relations

5. Speed Regulation

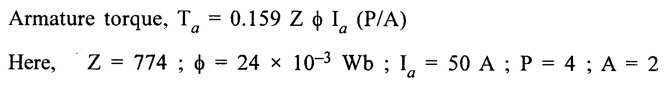

Basic Electrical and Electronics Engineering: Unit II: Electrical Machines : Tag: : - Torque and Speed Equations of DC Motors
Related Topics
Related Subjects
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation

