Hydraulics and Pneumatics: Unit II: Hydraulic Actuators and Control Components
some illustrative numerical problems
Hydraulic Actuators and Control Components - Hydraulics and Pneumatics
some illustrative numerical problems: Problems on Hydraulic Cylinders, Problems on Hydraulic Motors
SOME ILLUSTRATIVE NUMERICAL PROBLEMS Example 5.1 A hydraulic cylinder is to compress a car body in 8 seconds. The operation requires a stroke of 2.5 m and a force of 45,000 N. If a 8 N/mm2 pump has been selected, find the following: (i) Required piston area and piston diameter. (ii) The necessary pump flow. (iii) The hydraulic power capacity in kW. Given Data: t = 8s; L = 2.5 m; F = 45,000 N; P= 8 N/mm2. Solution: It is understood that this hydraulic system uses a single-acting hydraulic cylinder. (i) To find piston area (Ap) and piston diameter (D) : (ii) To find the pump flow rate (Qin) : (iii) To find the hydraulic power capacity in kW : Example 5.2 A press cylinder has to exert a force to lift the crosshead and tooling. The cylinder is rigidly fixed by front flange and the load is pivoted and fully guided. Maximum thrust from the press is 260 kN with a stroke of 1.4 m. Determine the size of suitable cylinder. The system working pressure should not exceed 200 bar. Given Data: F = 260 kN; Stroke = 1.4 m; Maximum system working pressure = 200 bar. Solution: The piston rod in a hydraulic cylinder will act as a strut when it is subjected to a compressive load or when it exerts a thrust. Therefore the rod must be of sufficient diameter to prevent buckling. So the suitable piston rod diameter to withstand buckling can be calculated using the following Euler's strut formula: where K = Bucking load in N, = Maximum load (F) × Factor of safety (S), E = Modulus of elasticity in N/m2, = 2.1 × 1011 N/m2 for steel. I = Moment of inertia of piston rod (m4), and = (π/64) d4, here d = Diameter of piston rod, L = Equivalent buckling length (m), Now applying Euler's formula, we get Example 5.3 A pump supplies oil at 1.5 Lps to a 50 mm diameter double-acting hydraulic cylinder. If the load is 4300 N (extending and retracting) and the rod diameter is 25 mm, find : (i) Hydraulic pressure during the extending stroke. (ii) Piston velocity during the extending stroke. (iii) Cylinder kW power during the extending stroke. (iv) Hydraulic pressure during the retracting stroke. (v) Piston velocity during the retracting stroke. (vi) Cylinder kW power during the retracting stroke. Given Data: Qin = 1.5 Lps = 1.5 × 10-3 m3/s; D = 50 mm; Fext = Fret = 4300 N; d = 25 mm. Solution: (i) To find the hydraulic pressure during the extending stroke (Pext): (ii) To find the piston velocity during the extending stroke (vext): (iii) To find the cylinder kW power during the extending stroke : (iv) To find the hydraulic pressure during the retracting stroke (Pret) : (v) To find the piston velocity during the retracting stroke (vret): (vi) To find the cylinder kW power during the retracting stroke : It may be noted that the cylinder supplies the more kW power during the retraction stroke than the extending stroke. Example 5.4 (i) The power and load carrying capacity of a hydraulic cylinder (Extension) are 10 kW and 20,000 N respectively. Find the piston velocity during extension. (ii) For the above system if the area of piston side and rod side is 2:1, find the retraction speed. The pump delivers oil at 0.2 m3/min. Given Data: Solution: (i) To find the piston velocity during extension: (ii) To find the retraction speed: First let us find Ap and Ar. Example 5.5 A single-vane rotary actuator has the following data : Outside radius of rotor = 12 mm; Outer radius of vane 38 mm; Width of vane = 25 mm; Hydraulic pressure developed = 70 bars Find: (i) the hydraulic force acting on the vane, and (ii) the torque generating capacity of the rotary actuator. Given Data: RR = 12 mm; RV = 38 mm; L = 25 mm; P = 70 bars = 70 × 105 N/m2 Solution: We know that the surface area of vane in contact with fluid, (i) To find the hydraulic force acting on the vane (F) : (ii) To find the torque capacity (T) : Example 5.6 A hydraulic motor has a 82 cm3 volumetric displacement. If it has a pressure valve setting for 70 bars and it receives oil from a 0.006 m3/s pump, find: (i) the motor speed, (ii) torque capacity, and (iii) power capacity of the motor. Given Data: VD = 82 cm3 = 82 × 10-6 m3; P= 70 bar = 70 × 105 N/m2; Q = 0.006 m3/s. Solution: (i) To find the motor speed (N) : (ii) To find the torque capacity (T) : (iii) To find the power capacity of the motor : Example 5.7 A hydraulic motor has a displacement of 150 cm3 and operates with a pressure of 85 bars and a speed of 1800 rpm. If the actual flow rate consumed by the motor is 5 Lps and the actual torque delivered by the motor is 185 N-m, find: (i) volumetric efficiency, (ii) mechanical efficiency, (iii) overall efficiency, and (iv) kW power delivered by the motor. Given Data: VD = 150 cm3 = 150 × 10-6 m3 ; P = 85 bars = 85 × 105 N/m2; N = 1800 rpm; QA = 5 Lps = 5 × 10-3 m3/s; TA = 185 N-m. Solution: First let us determine the theoretical flow rate. (i) To find the volumetric efficiency (ηmech) : (ii) To find the mechanical efficiency (ηmech): (iii) To find the overall efficiency (η0) : (iv) kW power delivered (i.e., actual power) by the motor : Example 5.8 A rotary vane air motor has a displacement volume of 80 cm3/rev and operates at 1750 rpm using 700 kPa gauge pressure air. Calculate the standard m3/min rate of consumption and kW power output of the motor. Assume the temperature remains constant. Given Data: VD = 80 cm3/rev; N = 1750 rpm; P = 700 kPa. Solution: It may be noted that the equations for determining the output torque and power for air motors are identical to those used for hydraulic motors. (1) To find m3/min rate of air consumption: (2) To find kW power output of motor:Problems on Hydraulic Cylinders


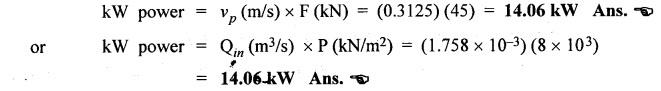
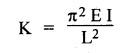




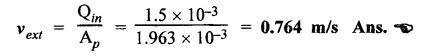

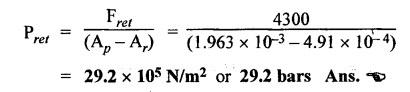
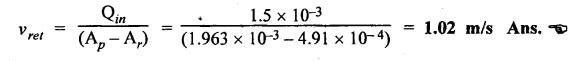




Problems on Hydraulic Motors


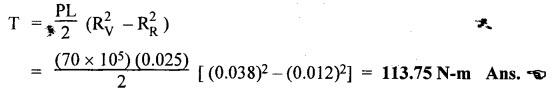
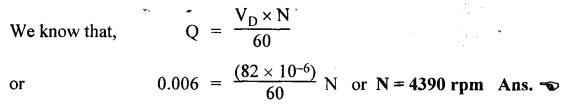

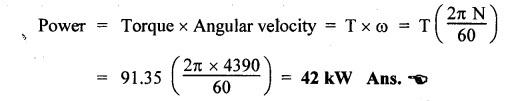

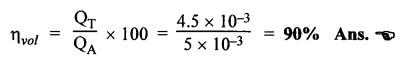
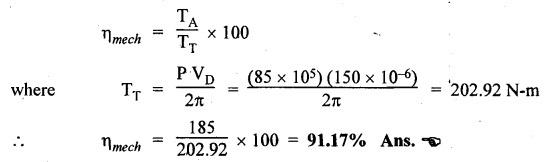




Hydraulics and Pneumatics: Unit II: Hydraulic Actuators and Control Components : Tag: : Hydraulic Actuators and Control Components - Hydraulics and Pneumatics - some illustrative numerical problems
Related Topics
Related Subjects
Hydraulics and Pneumatics
ME3492 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
