Materials Science: Unit II(a): Electrical Properties of Materials
Quantum Free Electron (GFE) Theory
Electrical and Magnetic Properties of Materials - Materials Science
The failures of classical free electron theory were rectified in quantum theory given by Sommerfeld in the year 1928.
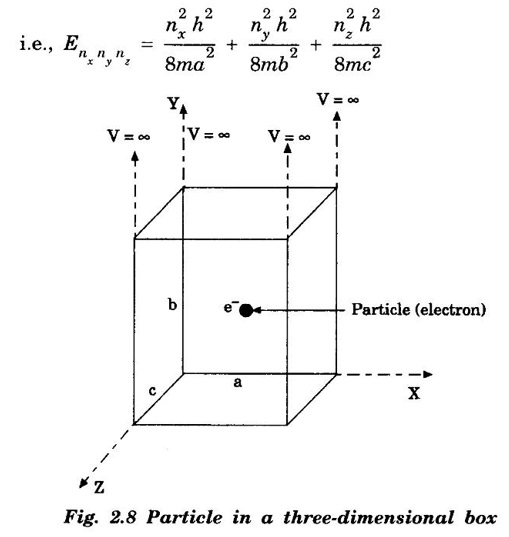
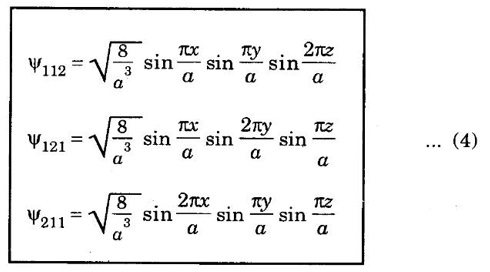
Success of Classical Free Electron Theory • It is used to verify Ohm's law. • It is used to explain electrical and thermal conductivities of metals. • It is used to derive Wiedemann-Franz law. • It is used to explain the optical properties of metals. • Classical theory states that all the free electrons absorb the supplied energy. But, the quantum theory states that only a few electrons absorb the supplied energy. • The electrical conductivity of semiconductors and insulators cannot be explained by this theory. • The photo-electric effect, Compton effect and black body radiation cannot be explained on the basis of classical free electron theory. • According to the classical free electron theory, the ratio K /σT is constant at all temperatures. But, it is found that it is not constant at low temperature. • According to this theory, the value of specific heat capacity of a metal is 4.5R. But, the experimental value is given by 3R. (Here R is the universal gas constant.) • The susceptibility of paramagnetic material is inversely proportional to temperature. But, the experimental result shows that paramagnetism of metal is independent of temperature. Moreover, ferro-magnetism cannot be explained by this theory. QUANTUM FREE ELECTRON (QFE) THEORY The failures of classical free electron theory were rectified in quantum theory given by Sommerfeld in the year 1928. This theory uses quantum concepts and hence it is known as quantum free electron theory. Sommerfeld used Schrodinger's wave equation and de-Broglie's concept of matter waves to obtain the expression for electron energies. He approached the problem quantum mechanically using Fermi Dirac statistics instead of classical Maxwell Boltzmann statistics. • The potential energy of an electron is uniform or constant within the metal. • The electrons have wave nature. • The allowed energy levels of an electron are quantized. • The electrons move freely within the metal and they are not allowed to leave the metal due to existance of potential barrier at its surfaces. • The free electrons obey Fermi - Dirac statistics. • This theory treats the electron quantum mechanically rather than classically. • It explains the electrical conductivity, thermal conductivity, specific heat capacity of metals, photoelectric effect and Compton effect, etc. • Even though it explains most of the physical properties of the metals, it fails to state the difference between conductor, semiconductor and insulator. • It also fails to explain the positive value of Hall coefficient and some of the transport properties of the metals. The solution of one-dimensional potential well is extended for a three-dimensional potential box. In a three-dimensional potential box, the particle (electron) can move in any direction in space. Therefore, instead of one quantum number n, we have to use three quantum numbers, nx, nx and nz, corresponding to the three coordinate axes namely x, y and z respectively. If a, b, c are the lengths of the box as shown in figure 2.8 along x, y and z axes, then Energy of the particle = Ex + Ey + Ez If a = b = c as for a cubical box, then The corresponding normalised wave function of an electron in a cubical box may be written as From the equations (1) and (2), we understand that several combinations of the three quantum numbers (nx, ny, and nz) lead to different energy eigen values and eigen functions. Example Suppose a state has quantum numbers, then nx = 1, ny = 1, nz = 2 Then, nx2 + ny2 + nz2 = 6 Similarly, for a combination nx = 1, ny = 2, nz = 1 and for acombination nx = 2, ny = 1, nz = 1 we have, nx2 + ny2 + nz2 = 6 The corresponding wave functions are written asFailures of Classical Free Electron (CFE) Theory
Postulates of Quantum Free Electron Theory
Merits of Quantum Free Electron Theory
Demerits of Quantum Free Electron Theory
Electrons in Metals Particle in a three dimensional box
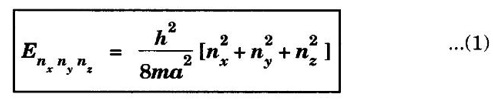
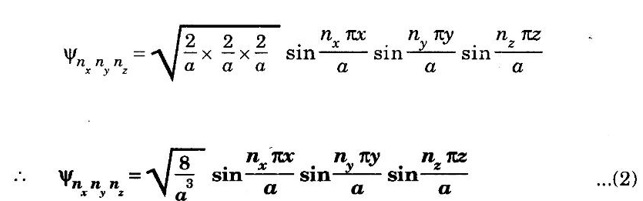
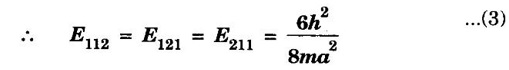
Materials Science: Unit II(a): Electrical Properties of Materials : Tag: : Electrical and Magnetic Properties of Materials - Materials Science - Quantum Free Electron (GFE) Theory
Related Topics
Related Subjects
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
