Miller Indices

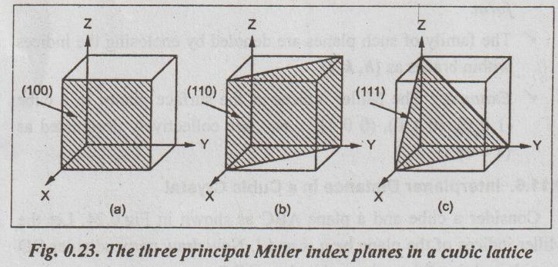
MILLER INDICES

✓ The orientation of a plane in a lattice is defined by the index of the plane. A set of numbers are used to identify the given planes. These set of numbers are known as miller indices.

✓ Miller evolved a method to designate a plane in a crystal by three numbers (h, k, l) known as Miller indices.

✓ Miller indices describe the angular position of planes with respect to the crystallographic axes but not their actual distances from the origin or any other selected point.

✓ Definition: Miller indices are the three smallest possible integers which have the same ratios as the reciprocals of the intercepts of the plane concerned on the three axes.

1. Procedure for Finding Miller Indices of Crystal Planes

The miller indices of a crystallographic plane are determined using the following procedure:

Step 1: Find the intercepts of the plane along the coordinate axes x, y and z.

Step 2: Express the intercepts in terms of axial units (i.e., x = pa, y = qb and z: rc).

Step 3: Find the reciprocals of the integers p, q and r. (i.e., 1/p, 1/q, 1/r).

Step 4: Convert these reciprocals into whole numbers by multiplying each one of them with their L.C.M.

Step 5: Enclose these integers in parenthesis. This represents the indices of the given plane.

Thus, Miller indices are the reciprocals of the intercepts, made by the plane on the illographic axes, when reduced to smallest integers.

2. Illustration

The above procedure is illustrated by considering the plane in Fig.0.22. The plane ABC has intercepts of 2 a on x-axis, 2 b on y-axis and 1 c on z-axis.

       x                    y             z

       2a                2b           1c

⸫   p = 2          q = 2       r = 1

Then the Miller indices of the plane ABC can be calculated as

Step 1: The intercepts are         2, 2, 1

Step 2: The reciprocal of intercepts are ½, ½, 1

Step 3: Taking LCM, we get     1,1,2

Step 4: The Miller indices of the plane ABC are (112)

3. Features of Miller Indices of Crystal Planes

The important features of the Miller indices are:

1. All the parallel planes have the same Miller indices. Thus the Miller indices define a set of parallel planes.

2. A plane parallel to one of the coordinate axes has an intercept of infinity.

3. If the Miller indices of two planes have the same ratio (i.e., 484 and 242 or 121), then the planes are parallel to each other.

4. Representation of Crystal Planes in a Cubic Unit Cell 

The principal crystallographic planes of cubic crystal structure are shown in Fig.0.23.

1. (100) Plane

The shaded plane in Fig.0.23 (a) has the intercepts 1, ∞, ∞ for the x, y and z-axes respectively. The reciprocals of the intercepts are 1, 0, 0. Thus Miller indices for this plane are (1 0 0). The plane is called one-zero-zero plane.

2. (110) Plane

The shaded plane in Fig.0.23 (b) has the intercepts 1, 1, ∞ whose reciprocals are 1, 1, 0. The miller indices are (1 1 0) and the plane is called one-one-zero plane.

3. (111) Plane

For the plane in Fig.0.23 (c), the intercepts are 1, 1, 1 which give Miller indices (1 1 1). This plane is called one-one-one plane.

Note

While finding Miller indices of the plane, the points to be kept in mind are:

(i) When a plane is parallel to one of the coordinate axes, it is said to meet that axis at infinity. Since 1/∞ = 0, the Miller index for that axis is zero. 

(ii) When the intercept of a plane is on the negative part of any axis, the Miller index is distinguished by a minus but directly over it.