Engineering Materials and Metallurgy: Unit 0: Review of Crystal Physics
Interplanar Distance in a Cubic Crystal
Consider a cube and a plane ABC as shown in Fig.0.24. Let the Miller indices of the plane be h, k and l.
Interplanar Distance in a Cubic Crystal Consider a cube and a plane ABC as shown in Fig.0.24. Let the Miller indices of the plane be h, k and l. Now draw perpendicular OD from the origin of the cube to the plane ABC. Let a = the lattice constant of the cube, dhkl = Perpendicular distance between the origin and the plane ABC i.e., the distance between two adjacent parallel planes having Miller indices (hkl), α, β and γ = Angles which the perpendicular makes with x, y and z axes respectively, and OA, OB and OC = Intercepts of the plane along x, y and z axes respectively. We know that the Miller indices of a plane are the smallest integers of the reciprocals of its intercepts. Therefore, the intercepts may also be expressed as reciprocals of Miller indices. From the geometry of the right angled triangles OAD, OBD and OCD, we get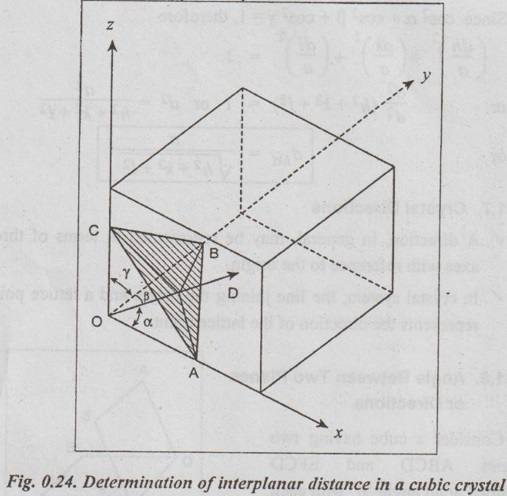
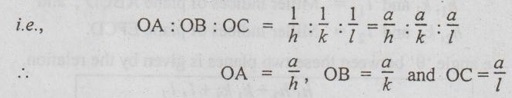
Engineering Materials and Metallurgy: Unit 0: Review of Crystal Physics : Tag: : - Interplanar Distance in a Cubic Crystal
Engineering Materials and Metallurgy: Unit 0: Review of Crystal Physics
Under Subject
Engineering Materials and Metallurgy
ME3392 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Materials and Metallurgy
ME3392 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Manufacturing Processes
ME3393 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation