Materials Science: Unit II(a): Electrical Properties of Materials
Expression for Thermal Conductivity of a Metal (Derivation)
Consider two cross-sections A and B of a metal rod separated by a distance λ.
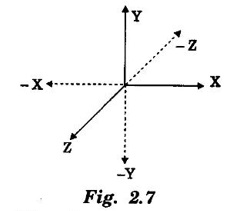
EXPRESSION FOR THERMAL CONDUCTIVITY OF A METAL (Derivation) Consider two cross-sections A and B of a metal rod separated by a distance λ. Let A be at a high temperature (T) and B at a low temperature (T – dT). Now, heat flows from A to B by the free electrons (Fig. 2.6) Conduction electron per unit volume = n Average velocity of the electrons = v During the movement of the electrons in the metal rod, the elastic collision takes place. Hence, the electrons near A lose their kinetic energy while electrons near B gain kinetic energy. where k - Boltzmann's constant T - Temperature at A. At B, average kinetic energy of the electron The excess of kinetic energy carried by the electron from A to B Number of electrons crossing per unit area per unit time from A to B = 1/6 nv ….. (4) The excess of energy carried from A to B per unit area in unit time. Similarly, the deficient of energy carried from B to A per unit area per unit time = 1/4 nuk dT ...(6) Let us assume that there is an equal probability for the electrons to move in all '6' directions as shown in the fig. 2.7. Each electron travels with thermal velocity v and n is the free electron per unit volume (density). Then, on an average 1/6 nv electrons travel in any one of the directions per unit area per unit time. Hence, the net amount of energy transferred from A to B per unit area per unit time But, from the definition of thermal conductivity, the amount of heat conducted per unit area per unit time Note: The students are not expected to write the part of the derivation given in the box in the examination. We know that for the metals relaxation time (τ) = collision time (τc) Substituting the eqn (9) in the eqn (8), we have The equation (10) is the expression for the thermal conductivity of a metal. Statement The ratio of thermal conductivity (K) to electrical conductivity (σ) is directly proportional to the absolute temperature (T). This ratio is constant for all metals at a given temperature. where L is a proportionality constant. It is known as Lorentz number. Its value is 1.12 × 10-8 WΩK-2 Derivation Wiedemann - Franz law is derived from the expressions of thermal and electrical conductivities of a metal. We know that Thermal conductivity of the metal Electrical conductivity of the metal The kinetic energy of the electron is given by Substituting eqn (4) in eqn (3), we have Thus, it is proved that the ratio of thermal conductivity to electrical conductivity of the metal is directly proportional to the absolute temperature of the metal. This law is verified experimentally and it is found to hold good at normal temperature. But, this law is not applicable at very low temperature. Wiedemann - Franz law clearly shows that if a metal has high thermal conductivity, it should also have high electrical conductivity. Among the metals, the best electrical conductors (silver, copper, aluminium) are also the best conductors of heat. The ratio of thermal conductivity (K) to the product of electrical conductivity (σ) and absolute temperature (T) of the metal is a constant. It is known as Lorentz number and it is given by Substituting for Boltzmann's constant k = 1.38 × 10-23 JK-1 and the charge of the electron e = 1.602 × 10-19 coulomb, we get Lorentz number as It is found that the value of Lorentz number determined using classical free electron theory is only half of the experimental value i.e., 2.44 × 10-8 WΩK-2. This discrepancy in experimental and theoretical values of Lorentz number is one of the failures of the classical theory. It is rectified in quantum theory.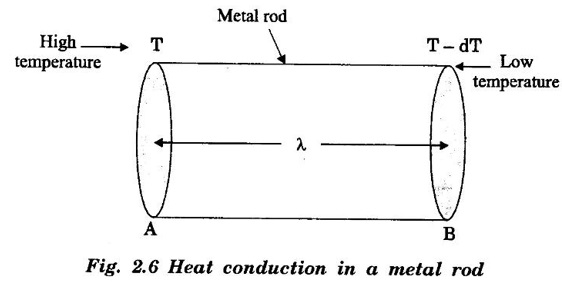
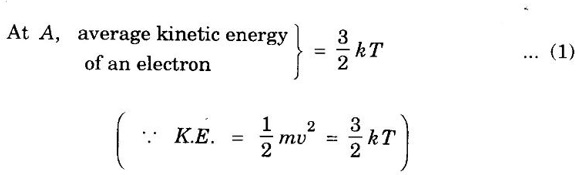

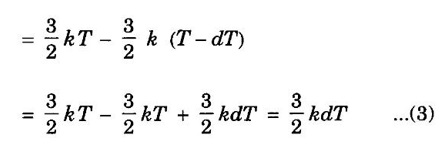

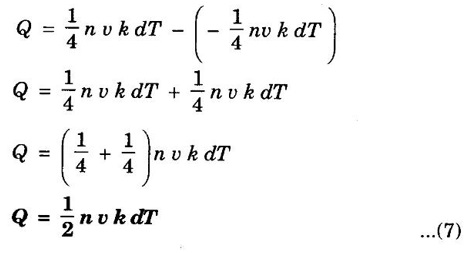

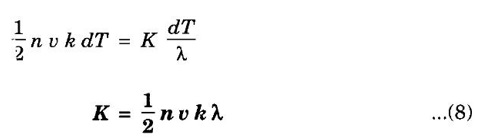
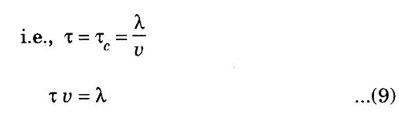
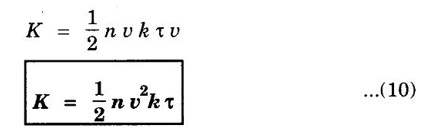
Wiedemann - Franz Law
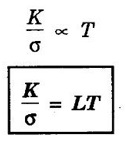




Conclusion
Lorentz Number
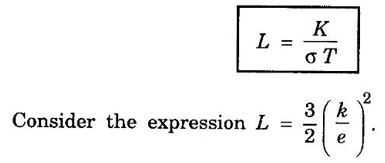
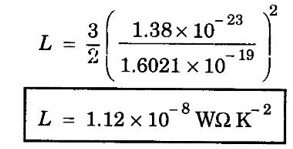
Materials Science: Unit II(a): Electrical Properties of Materials : Tag: : - Expression for Thermal Conductivity of a Metal (Derivation)
Related Topics
Related Subjects
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
