Engineering Graphics: Unit I (b): Scales
Diagonal Scale
Examples | Engineering Graphics (EG)
A diagonal scale is used to represent three consecutive units. ie., First unit (main unit), second unit (sub unit) and third unit (sub division of second unit).
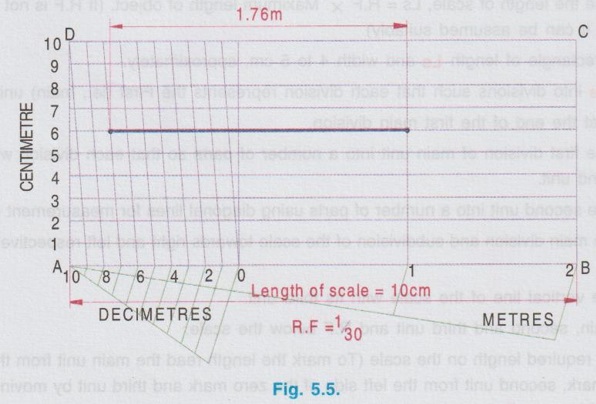
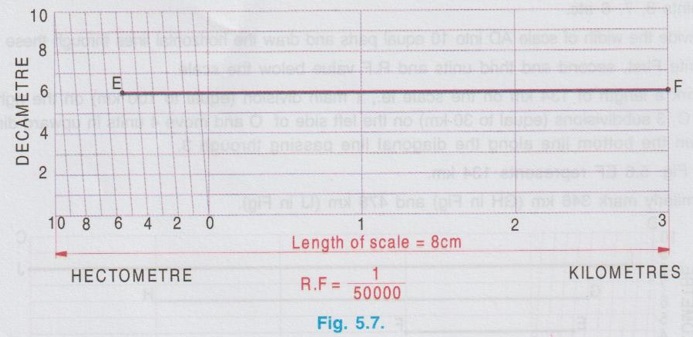
DIAGONAL SCALE A diagonal scale is used to represent three consecutive units. ie., First unit (main unit), second unit (sub unit) and third unit (sub division of second unit). Examples: 1. Metre, decimetre and centimetre (1 metre = 10 decimetre ; 1 decimetre = 10 centrimetre) 2. Kilometre, hectometre and decametre (1 kilometre = 10 hectometre ; 1 hectometre = 10 decametre) 3. Decimetre, centimetre and millimetre (1 decimetre = 10 centimetre ; 1 centimetre = 10 millimetre) 4. Yard, feet and inches (1 yard = 3 feet ; 1 foot = 12 inches) In diagonal scales also the length of scale is at first divided into main division and subdivision as drawn in plain scale. Further, each unit of subdivision to be divided into equal number of divisions of subunit (ie., third unit). But it is very difficult to subdivide the second unit, hence a diagonal line is drawn connecting two consecutive subdivisions and the horizontal lines are drawn along the width of scale to intersect the diagonal line. The perpendicular drawn through the points of intersection on diagonal line will divide the subunit into required number of subdivisions. Let AB represents the second unit required be divided into say 10 divisions of third unit as shown in Fig. 5.4. Draw verticals at A and B along the width of scale to locate the points C and D respectively. Let the second unit AB to be divided into 10 equal parts. Instead of dividing the line AB into 10 equal parts, draw the diagonal AD and divide the width of scale AC into 10 equal parts and name the parts as 1, 2, 3 etc. marking from A. Now draw the horizontal lines through these points to intersect the diagonal AD at 1', 2', 3' etc., respectively. If a vertical line is drawn through 1' to the base AB, it will intercept AB at 1''. clearly Thus the horizontal intercepts (1 - 1', 2 - 2', 3 - 3' etc.) are progressively greater in length by 1/10 AB. Hence the diagonal line AD facilitate the division of second unit to obtain third unit. The following steps are followed for the construction of a diagonal scale. 1. Decide First, second and third units. 2. Determine the length of scale, Ls = R.F × Maximum length of object. (If R.F is not given in the problem, it can be assumed suitably) 3. Draw a rectangle of length Ls and width 4 to 5 cm, approximately. 4. Divide Ls into divisions such that each division represents the First (ie., main) unit. 5. Mark O at the end of the first main division. 6. Divide the first division of main unit into a number of parts so that each division will represent the second unit. 7. Divide the second unit into a number of parts using diagonal lines for measurement of third unit. 8. Label the main division and subdivision of the scale towards right and left respectively from zero mark 9. Label the vertical line of the scale with its third unit. 10. Write Main, second and third unit and R.F below the scale. 11. Mark the required length on the scale (To mark the length read the main unit from the right side of zero mark, second unit from the left side of the zero mark and third unit by moving in upward direction along the diagonal line). Example 5 : Construct a diagonal scale of R.F 1 : 30 to read metres, decimetres and centimetres and long enough to measure upto 3m. Also mark a length of 1.76 m on the scale. Data given : R.F = 1/30 ; Maximum length = 3m Main, second and third units are, metre, decimetre and centimetre respectively. 1. Length of scale, Ls = R.F × Maximum length = 1/30 × 3m = 1/30 × 3 × 100 cm = 10 cm. 2. Draw a rectangle having length AB = 10 cm and width 4 cm (assumed) 3. Divide the length of scale (ie., 10 cm) into 3 equal parts so that each part will represent 1 metre. 4. Mark O at the end of first main division, and the other divisions as 1 and 2 towards right. 5. Divide the first main division into 10 equal parts so that each subdivision will represent 1 decimetre. Mark the sub divisions as 1, 2, 3 etc. from O towards left. 6. Draw the diagonal line joining the point 9 and D (D is the point marked on the other side of scale drawn vertical through A) and draw the parallel diagonal lines through the remaining points 8, 7 etc., 7. Divide the width of scale AD also into 10 equal parts and draw the horizontal lines through these points. Name the parts 1, 2, 3 etc. from A, bottom to top. 8. Write main, second and third unit and R.F value below the scale. 9. Mark a length of 1.76 m on the scale, ie., 1 m on the right side of the zero mark 7 decimetre on the left side of zero mark and move 6 units in upward direction from the bottom line along the diagonal line passing through 7. The scale is shown in Fig. 5.5. Example 6 : The distance between Chennai and Coimbatore is 500 km. It is represented by a distance of 10 cm on a map. Find R.F and construct a diagonal scale to read kilometres. Also show distances of 346 km, 134 km and 478 km. Maximum distance to be measured by the scale is not given in the problem. Hence it can be assumed suitably. Since the longest distance to be measured is 468 km, construct a diagonal scale to measure maximum distance as 500 km. First, second and third units are 100 km, 10 km and 1 km respectively. 1. Length of scale, Ls = R.F × Maximum length = 1/ 5 × 106 × 500 km = 1 / 5 × 106 × 500 × 1000 × 100 cm = 10 cm 2. Draw a rectangle having length AB = 10 cm and width 4 cm (assumed) 3. Divide the length of scale into 5 equal parts so that each part will represent 100 km. 4. Point O at the end of first main division and the other divisions as 1, 2, 3 and 4 towards right (4 coincides with B). 5. Divide the first main division A-O into 10 equal parts so that each subdivision will represent 10 km. Mark the subdivisions as 1, 2, 3 etc. from O towards left. 6. Draw the diagonal line joining the point 9 and D (D is the point marked on the other side of scale drawn perpendicular through A) and draw parallel diagonal lines through the remaining points 8, 7, 6 etc. 7. Divide the width of scale AD into 10 equal parts and draw the horizontal lines through these points. 8. Write First, second and thrid units and R.F value below the scale. 9. Mark a length of 134 km on the scale ie., 1 main division (equal to 100 km) on the right side of O, 3 subdivisions (equal to 30 km) on the left side of O and move 4 units in upward direction from the bottom line along the diagonal line passing through 3. In Fig. 5.6 EF represents 134 km. 10. Similarly mark 346 km (GH in Fig) and 478 km (IJ in Fig). Example 7 : A rectangular map of size 20 cm x 5 cm represents an area of 25 square kilometres. Construct a diagonal scale to measure kilometres, hectometres and decametres and show on it a distance of 3 km, 5 hm and 6 dm. It is given that 20 cm × 5 cm ie., 100 cm2 area represents 25 square kilometres. since the maximum distance to be measured is 3 km, 5 hm and 6 dm diagonal scale can be constructed to measure upto 4 km. First unit as kilometre Second unit as hectometre (1 kilometre = 10 hectometre) Third unit as decametre (1 hectometre = 10 decametre) ⸫ Length of scale, Ls = R.F × Maximum distance to be measured = 1 / 50000 × 4 × 1000 ×100 cm = 8 cm The diagonal scale is constructed as shown in Fig. 5.7. and a distance of 3 km, 5 hm and 6 dm is marked on the scale, represented by a line EF.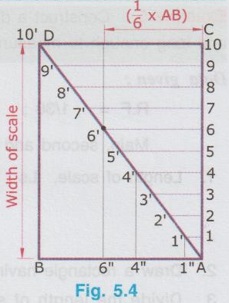

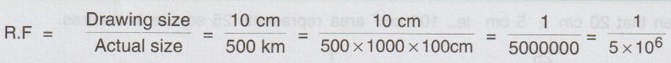


Engineering Graphics: Unit I (b): Scales : Tag: : Examples | Engineering Graphics (EG) - Diagonal Scale
Related Topics
Related Subjects
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
