Atomic Packing Factor (APF)

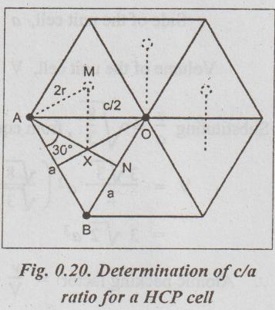
Atomic Packing Factor (APF)

✓ Atomic packing factor is defined as the ratio of the volume of the atoms per unit cell to the total volume occupied by the unit cell.

✓ It is also known as relative density of packing or atomic packing density.

Calculation of APF:

Atomic packing factor can be calculated as follows in various crystal structures.

1. Simple Cubic (SC) structure

Number of atoms per unit cell = 1

Volume of one atom, v =  4/3 π r3

Side of the unit cell, a = 2 r

Volume of the unit cell, V = a3

Atomic packing factor, APF = v/V = ( 4/3 π r3) / a3

We know that for SC lattice, r = a/2

2. Body Centred Cubic (BCC) structure

Number of atoms per unit cell = 2

3. Face Centred Cubic (FCC) structure

Number of atoms per unit cell = 4

4. Hexagonal Close Packed (HCP) structure

In order to calculate APF for HCP structure, first we have to find the volume of the unit cell and c/a ratio.

Step 1: Volume of the unit cell, V

✓ The volume of the unit cell may be determined by computing the area of the base of the unit cell and then by multiplying it by the cell height.

✓ The area of the base of the unit cell is the area of the hexagon ABDEFG, as shown in Fig.0.19 (a). It is equal to the sum of the areas of the six equal sized triangles.

where

c = Height of the unit cell, and

a = Distance between two neighbouring cells.

Step 2: Calculation of с / a ratio

✓ The three body atoms lie in a horizontal plane at a height cla from the orthocentres of alternate equilateral triangles in the base or at top of the hexagonal cell, as shown in Fig.0.20.

✓ In the triangle ABN,

cos 30° = AN / AB

Step 3: Calculation of Atomic Packing Factor

Number of atoms per unit cell = 6

Thus the density of packing is 74% and hence it is a close packed structure.