Materials Science: Unit II(a): Electrical Properties of Materials
Anna University Solved Problems
Electrical Properties of Materials | Materials Science
Anna University Solved Problems: Problems with solutions: Electrical and Magnetic Properties of Materials - Materials Science
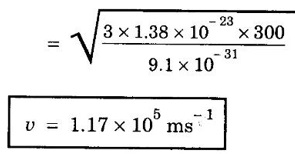
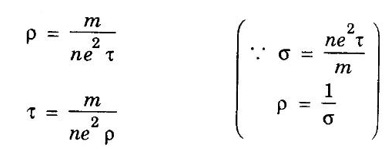
ANNA UNIVERSITY SOLVED PROBLEMS Problem 2.4 Calculate electrical conductivity in copper if the mean free path of electrons is 4 × 10-8 m, electron density is 8.4 × 1028 m-3 and average thermal velocity of electron is 1.6 × 106 ms-1. Given data Mean free path of electron λ = 4 × 10-8 m Electron density n = 8.4 × 1028 8.4 m-3 Average thermal velocity of the electrons v = 1.6 × 10 ms-1 Charge of an electron e = 1.6 × 10-19 coulomb Mass of an electron m = 9.11 × 10-31 kg Solution Problem 2.5 Calculate electrical and thermal conductivities for a metal with a relaxation time 10-14 second at 300 K. Also, calculate Lorentz number using the above result (density of electrons = 6 × 1028 m-3 ). Given data Relaxation time τ = 10-14 s Temperature T = 300 K Electron concentration n = 6 × 1028 m-3 Mass of an electron m = 9.1 × 10-31 kg Charge of an electron e = 1.6 × 10-19 C Boltzmann's constant k = 1.38 × 10-23 JK-1 Solution We know that σ = Substituting the given values, we have Electrical conductivity σ = 1.69 × 107Ω-1 m-1 Thermal conductivity K = (By quantum free electron theory) Substituting the given values, we have K = 123.80 W m-1K-1 Problem 2.6 Find the relaxation time of conduction electrons in a metal of resistivity 1.54 × 10-8 ohm-m if the metal has 5.8 × 1028 conduction electrons / m3. Given data Number of electrons / unit volume n = 5.8 × 1028 m-3 Resistivity of the metal ρ = 1.54 × 10-8 Ω m Solution We know that the electrical conductivity of a metal Substituting the given values, we have Problem 2.7 A uniform silver wire has a resistivity of 1.34 × 10-8 Ω m at room temperature for an electric field of 1 volt/cm. Calculate (i) the drift velocity (ii) the mobility and (iii) the relaxation time of electrons assuming that there are 5.8 × 1028 conduction electrons m-3 of the material. Given data Resistivity of the wire ρ = 1.34 × 10-8 Ω m Electrical field E = 1V/cm = 1V / 10-2 m = 1 × 102 Vm-1 Number of electron per unit volume n = 5.8 × 1028 m-3 Solution Problem 2.8 Calculate the drift velocity and thermal velocity of conduction electrons in copper at a temperature of 300 K. When a copper wire of length of 2 m and resistance 0.02 Ω carries a current of 15 A. Given mobility μ = 4.3 × 10-3 m2V-1s-1 Given data Temperature T = 300 K Length of the wire L = 2 m Resistance R = 0.02 Ω Current I = 15 A Mobility μ = 4.3 × 10-3 m2 V-1s-1 Solution Voltage drop V across the wire is V = IR = 15 × 0.02 = 0.3 V Electric field E across the wire is given by Drift velocity Substituting the given values, we have Problem 2.9 Find the drift velocity of the free electrons in a copper wire whose cross sectional area is 1.0 mm2 when the wire carries a current of 1A. Assume that each copper atom contributes one electron to the electron gas. Given n = 8.5 × 1028 m-3. Given Data Conduction electron / m3, n = 8.5 × 1028 m-3 Charge of electron e = 1.6 × 10-19 C Area of cross section A = 1.0 × 10-6 m2 Current I = 1.0 A Solution The drift velocity of the free electrons is given by Substituting the given values, we have Problem 2.10 A metallic wire has a resistivity of 1.42 × 10-8 Ω m. For an electric field of 0.14 V/m. Find (i) average drift velocity and (ii) mean collision time, assuming that there are 6 × 1028 electrons / m3. Given data Electric field E = 0.14 Vm-1 Resistivity ρ = 1.42 × 10-8 Ω m Number of electrons per unit volume n = 6 × 1028 m-3 Charge of the electron e = 1.6 × 10-19 C Mass of an electron m = 9.1 × 10-31 kg Solution: The resistivity of a metal is given by, Substituting the given values, we have Problem 2.11 Calculate the number of states lying in an energy interval of 0.01 eV above the Fermi level for a crystal of unit volume with Fermi energy EF = 3 eV Given data Mass of electron m = 9.1 × 10-31 kg Energy interval ΔE = 0.01 eV Planck's constant h = 6.63 × 10-34 Js Fermi energy EF = 3 eV [⸪ 1 eV = 1.6 × 10-19 J] EF = 3 × 1.6 × 10-19 J EF = 4.8 × 10-19 J Solution: We know that ΔE = E - EF = EF + ΔE = (3 + 0.01) eV = 3.01 × 1.6 × 10-19 J E = 4.816 × 10-19 J Number of states per unit volume lying between EF and E is given by Substituting the given values, we have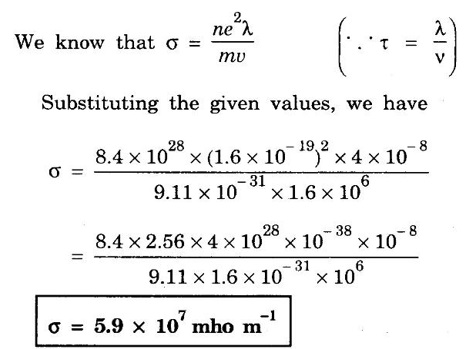
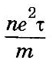
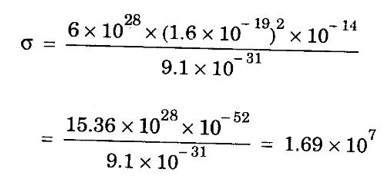
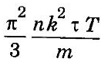
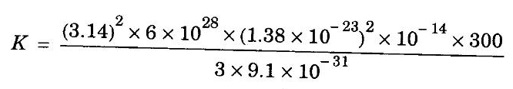
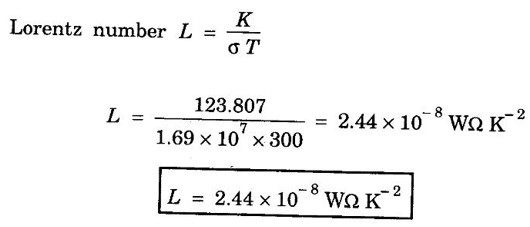
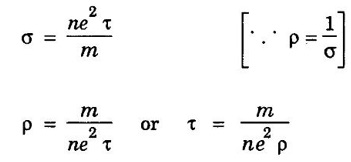
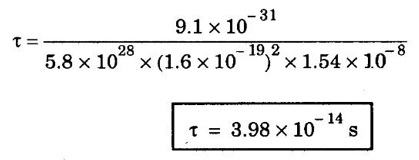

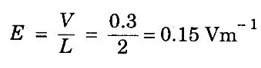
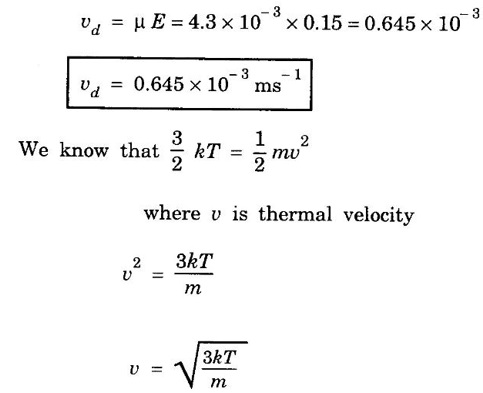
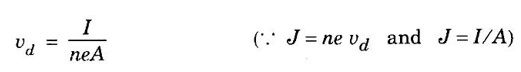
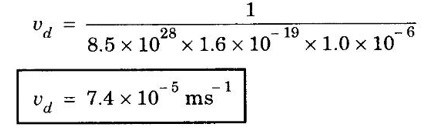

Density of energy states
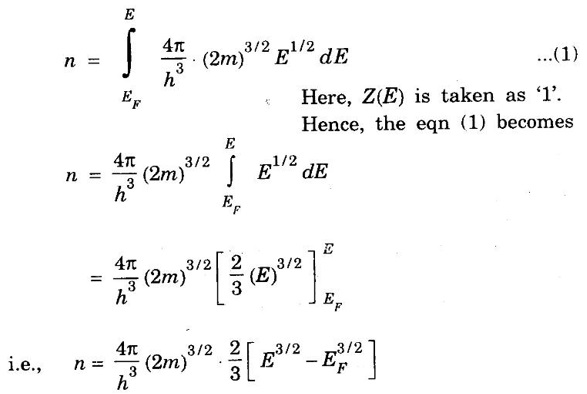
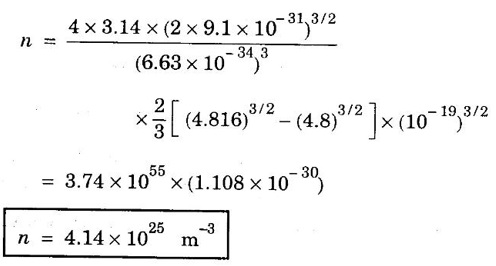
Materials Science: Unit II(a): Electrical Properties of Materials : Tag: : Electrical Properties of Materials | Materials Science - Anna University Solved Problems
Related Topics
Related Subjects
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
