Materials Science: Unit II(a): Electrical Properties of Materials
Anna University Solved Problems [Lorentz number]
Anna University Solved Problems: Electrical and Magnetic Properties of Materials - Materials Science
ANNA UNIVERSITY SOLVED PROBLEMS Problem 2.1 The electrical resistivity of copper at 27 °C is 1.72 × 10-8 Ω m. Compute its thermal conductivity if the Lorentz number is 2.26 × 10-8 W Ω K-2. Given data Electrical resistivity ρ = 1.72 × 10-8 Ω m Temperature T = 27°C = 27 + 273 = 300 K Lorentz number L = 2.26 × 10-8 W Ω K-2 Solution We know that Wiedemann - Franz law Substituting the given values, we have Problem 2.2 The thermal and electrical conductivities of copper at 20°C are 390 Wm-1K-1 respectively. Calculate Lorentz number. Given data Thermal conductivity of copper K = 390 Wm-1K-1 Electrical conductivity of copper σ = 5.87 × 107Ω-1 m-1 Temperature T = 20°C = (20 +273) = 293 K Solution We know that Lorentz number L = K / σT Substituting the given values, we have • It is used to verify Ohm's law. • It is used to explain electrical and thermal conductivities of metals. • It is used to derive Wiedemann-Franz law. • It is used to explain the optical properties of metals. • Classical theory states that all the free electrons absorb the supplied energy. But, the quantum theory states that only a few electrons absorb the supplied energy. • The electrical conductivity of semiconductors and insulators cannot be explained by this theory. • The photo-electric effect, Compton effect and black body radiation cannot be explained on the basis of classical free electron theory. • According to the classical free electron theory, the ratio K /σT is constant at all temperatures. But, it is found that it is not constant at low temperature. • According to this theory, the value of specific heat capacity of a metal is 4.5R. But, the experimental value is given by 3R. (Here R is the universal gas constant.) • The susceptibility of paramagnetic material is inversely proportional to temperature. But, the experimental result shows that paramagnetism of metal is independent of temperature. Moreover, ferro-magnetism cannot be explained by this theory.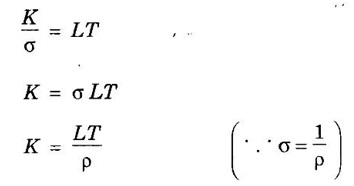
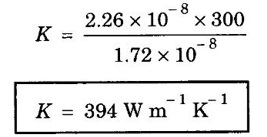
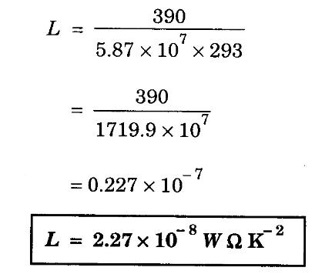
Success of Classical Free Electron Theory
Failures of Classical Free Electron (CFE) Theory
Materials Science: Unit II(a): Electrical Properties of Materials : Tag: : - Anna University Solved Problems [Lorentz number]
Related Topics
Related Subjects
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
