Materials Science: Unit II(a): Electrical Properties of Materials
Anna University Solved Problems [Fermi distribution function]
Anna University Solved Problems: Problems with solutions: Materials Science: Electrical and Magnetic Properties of Materials
ANNA UNIVERSITY SOLVED PROBLEM Problem 2.3 Use Fermi distribution function to obtain the value of F(E) for E -EF = 0.01 eV at 200 K. Given data E -EF = 0.01 eV = 0.01 × 1.6 × 10-19 J = 1.6 × 10-21 J Temperature T = 200 K Boltzmann's constant k = 1.38 × 10-23 JK-1 Solution Substituting the given values, we have F(E) = 0.359 The dependence of Fermi distribution function on temperature and its effect on the occupancy of energy level is shown in fig. 2.10 (a) and (b). Thus at T = 0 K, there is 100% chance for the electrons to occupy the energy levels below Fermi energy level ie., all the energy levels are occupied by the electrons. Thus, there is 0% chance for the electrons to occupy the energy level above Fermi energy level ie., all the energy levels above Fermi energy level are not occupied by the electrons (empty). From the above two cases, at T = 0 K the variation of F (E) for different energy values become a step function as shown in tig 2.10(a). Case (iii) Probability of occupation at ordinary temperature At ordinary temperature, the value of the probability function starts reducing from 1 for energy values E slightly less than EF. With the increase of temperature, i.e., T > 0 K, Fermi function F (E) varies with E as shown in fig. 2.10(b). At any temperature other than OK and E = EF. % of F(E) = 0.5 × 100 = 50% Hence, there is 50% chance for the electrons to occupy Fermi energy level ie., the value of F(E) becomes 1/2 at E = EF This result is used to define Fermi energy level. Fermi energy level • It is the energy level at any finite temperature above 0 K at which the probability of electron occupation is 1/2 or 50%. • It is also the energy level of maximum energy of the filled states at 0 K. Further for E > EF, the probability value falls off rapidly to zero (Fig 2.10(b)). Case (iv) At high temperature When kT >> EF or T → ∞, the electrons lose their quantum mechanical character. Now, Fermi distribution function reduces to classical Boltzmann distribution. Uses of Fermi distribution function • It gives the probability of an electron occupancy for a given energy level at a given temperature. • It is very useful to find the number of free electrons per unit volume at a given temperature. • It is used to find Fermi energy of the metal.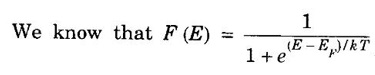

Effect of Temperature on Fermi Function



Materials Science: Unit II(a): Electrical Properties of Materials : Tag: : - Anna University Solved Problems [Fermi distribution function]
Related Topics
Related Subjects
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
