Engineering Physics: Unit II: Electromagnetic Waves
Wave Equation
Maxwell's equations | Electromagnetic Waves
Plane Electromagnetic Wave Equation in Vacuum Maxwell's equations in general form are
WAVE EQUATION Plane Electromagnetic Wave Equation in Vacuum Maxwell's equations in general form are Now, for the free space (vacuum) the permittivity and permeability are denoted by ε0 and μ0, respectively. Therefore, Also, the conductivity σ = 0, that is the medium is a perfect insulator. Therefore there is no conduction current in the medium which implies Also there is no charge present in the vacuum therefore ρ = 0 and as a result eqn.(1) reduces to Wave equation for electric field vector Taking the curl on both sides of equation (3), we get Now from vector calculus identity, we have But from eqn. (5), substituting eqn (8) in eqn (6) This is general electromagnetic wave equation in terms of electric field vector Wave equation for magnetic field vector Taking curl on both sides of the equation (4), we have Now from vector calculus identity, we have But from eqn (2), we have Substituting eqn (13) in eqn (12), we get on substituting eqn (14) in eqn (11), we have Using eqn (14) and eqn (11) Substituting the eqn (3) in eqn (15) This general electromagnetic wave equation in terms of 1. The electromagnetic wave equation for In one dimension say along x-axis, the wave equations are given by the x-components of the above expression. That is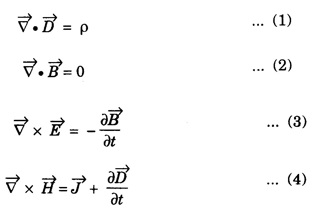


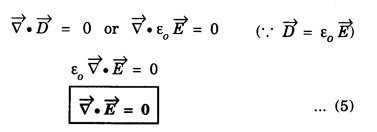
![]()
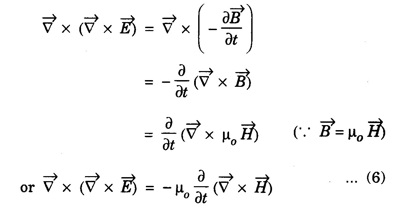
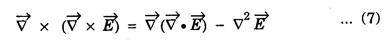
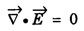 and substituting this in equation (7) we get
and substituting this in equation (7) we get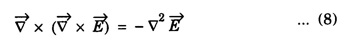

![]() for free space.
for free space.![]()

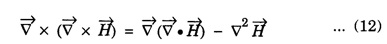
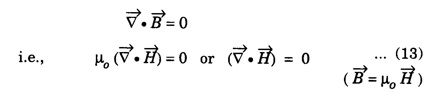
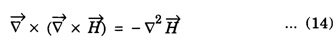
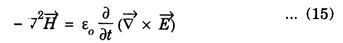
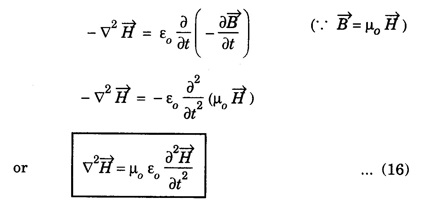
![]() for free space.
for free space.Discussion
![]() and
and ![]() is written as
is written as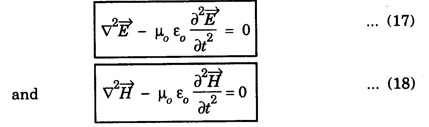
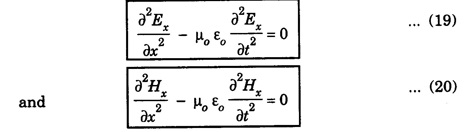
Engineering Physics: Unit II: Electromagnetic Waves : Tag: : Maxwell's equations | Electromagnetic Waves - Wave Equation
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
