Engineering Mechanics: Unit I: Statics of Particles
Vector Addition
law, Solved Example Problems
Vector addition can be performed using the following methods
Vector Addition Vector addition can be performed using the following methods a) Triangle law b) Polygon law c) Parallelogram law d) Resolution and composition. 1. Triangle Law If two vectors are represented in magnitude and direction by two sides of a triangle taken in order, their resultant is represented in magnitude and direction by the third side of the triangle drawn from starting point of first vector to end point of second vector. • Triangle law can be used for graphical solution as well as analytical solution. • For graphical solution, the given vectors • For analytical solutions sine rule or cosine rule can be used after completing the triangle. For reference, sine rule and cosine rule are given in Fig. 1.8.2. Note: Triangle law can be used to find resultant of only two vectors at a time. 2. Polygon Law If more than two vectors are represented in magnitude and direction by sides of an incomplete polygon taken in order, their resultant is represented in magnitude and direction by the remaining side of the polygon, drawn from starting point of first vector to end point of last vector • This law is a generalization of triangle law for more than two vectors. • If five vectors • This method is used for graphical solution where all given vectors are drawn to scale. The resultant magnitude is obtained by measuring the length of the last side and converting it back to scale. The direction is obtained by measuring the angle of resultant with any reference direction (generally the horizontal direction). 3. Parallelogram Law It two vectors are represented in magnitude and direction by two adjacent sides of a parallelogram, their resultant is represented in magnitude and direction by the diagonal of the parallelogram drawn from their common point. If Proof : • The two given vectors • The diagonal AC represents the resultant The line AD is extended and a perpendicular is drawn from C on this line. As ABCD is a parallelogram, • Parallelogram law can be used to find resultant of two vectors. It can be used to obtain solution either analytically or graphically. • For analytical solution, equations (1.8.1) and (1.8.2) are used. For graphical solution, the parallelogram is constructed to scale and magnitude of 4. Resolution and Composition • The process of replacing a vector by two or more vectors (known as components) which produce the same effect as that produced by the single vector is known as resolution. • A vector can be resolved into any number of components. • Composition is a process in which two or more vectors are replaced by a single vector (known as resultant) which produces the same effect as that produced by all the vectors together. • Although a vector can be resolved into any number of components along any directions in space, they are generally resolved into two mutually perpendicular components in two dimensions and three mutually perpendicular components in three dimensions. • This helps in setting up scalar equations which are easier to solve. In two dimensions, the scalar equations along X direction can be solved independent of equations along Y direction. The vector results can then be obtained using composition. 5. Resolution and Composition of Vectors in a Plane (Two Dimensions) • Vectors can be resolved into two mutually perpendicular directions (not necessarily horizontal and vertical). The two perpendicular directions can be assumed to be the X and Y axes. • To resolve any vector of magnitude F draw lines parallel to the required X and Y-directions from base of the vector. The two camponents will be adjacent to the vector. Find angle say ' θ ', of vector with either X or Y-axis. • The magnitude of component adjacent to that angle will be F cos θ and the other perpendicular component will be F sin θ. The sign of these components will depend on whether they are along positive or negative co-ordinate axes. • Alternatively, one can find the angle θ with positive X-axis measured in anticlockwise sense and use F cos θ and F sin θ as X and Y-components respectively. without assigning any sign. • If the vector is either along X or Y-direction, it will have only one component and the other will be zero. For example, if a vector is along X-direction, its Y-component will be zero. • These concepts are illustrated in the following examples: • After finding the X and Y components the vector can be writ n-in terms of unit vectors î and ĵ as where Ax and Ay are the X and Y components of (1.8.3) • If Ax and Ay are known, the magnitude and direction of • The symbolic representations of the four quadrants are shown in Fig. 1.8.6. Note that only an arrow is shown and the value of ✪ is not written when either X or Y component is zero. 6. Resolution and Composition of Vectors in Three Dimensions • The X, Y and Z components of vectors can be written in three dimensions in different ways depending upon how the data is given. These different cases are discussed below. 1) If a vector is parallel to one of the co-ordinate axes, it will have only one non-zero component along that axis and the remaining two components will be zero. • For the three vectors shown in Fig. 1.8.7. Similarly, 2) If angle made by a vector with one of the co-ordinate axes is given and the angle made by its projection in a plane with one of the co-ordinate axes in that plane is given, resolve the vector into two mutually perpendicular components. i) A component along the axis with which angle of vector is given, and ii) The perpendicular component which is the projection of vector in the plane of the remaining two axes. • Then resolve the projection along the two axes in the plane of the projection. • For the vector Ay = A cos θ and projection in XZ-plane is A sin θ. • Resolving A sin θ along X and Z directions, Ax = A sin θ sin ϕ and Az = A sin θ cos ϕ. 3) If a vector 4) If a vector An important relation satisfied by the direction cosines is cos2 θx + cos2 θy + cos2 θz = 1 ….(1.8.12) 7. Scalar Product or Dot Product of Two Vectors • If 'θ', is the angle between two vectors • If two vectors are perpendicular then their dot product is zero. The angle between two vectors can be obtained using the dot product as • Geometrical interpretation of dot product : If 8. Vector Product or Cross Product of Two Vectors • If • Right handed screw rule: If a right handed screw is placed perpendicular to both • Right hand rule: If fingers of the right hand are curled from • Geometrical interpretation of cross product : i) If ii) If 9. Scalar Triple Product The scalar triple product of three vectors Solved Examples for Understanding Example 1.8.1 Solution : Example 1.8.2 Show that the vectors Solution: If two vectors are parallel, their cross product is zero. Example 1.8.3 Determine the unit vector along the line which orginates at the point (4, 1,-2) and passes through the point (2, 2, 6). Solution: Example 1.8.4 If vector 1) Find ii) Find the included angle between vector Solution: i) Example 1.8.5 With respect to origin (0, 0, 0), a point A is located at (-5, 2, 14). Specify the position of the point. a) In terms of orthogonal components, b) In terms of directional cosine, and c) In terms of unit vector. Solution: a) The x, y, z components of A are x = - 5, y = 2, z = 14 Hence position vector of A can be written as b) The direction cosines are Example 1.8.6 Solution: Example 1.8.7 Find Solution: Example 1.8.8 Find the angle between the forces A and B given as Solution: 
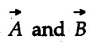 are to be drawn to scale in the given directions. The length of the third side, converted back to scale gives magnitude of the resultant and direction is obtained by measuring the angle with horizontal or with any of the given vectors.
are to be drawn to scale in the given directions. The length of the third side, converted back to scale gives magnitude of the resultant and direction is obtained by measuring the angle with horizontal or with any of the given vectors.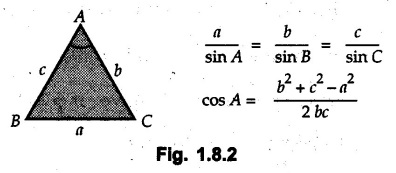
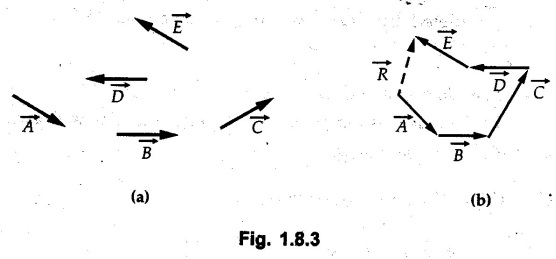
 are given as shown their resultant
are given as shown their resultant 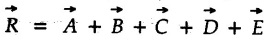 is obtained by drawing them one after the other as shown in Fig. 1.8.3 (b). The last side, which completes the polygon, represents the resultant in magnitude and direction.
is obtained by drawing them one after the other as shown in Fig. 1.8.3 (b). The last side, which completes the polygon, represents the resultant in magnitude and direction. are two vectors and α is the angle between them then the magnitude of their resultant is given by,
are two vectors and α is the angle between them then the magnitude of their resultant is given by,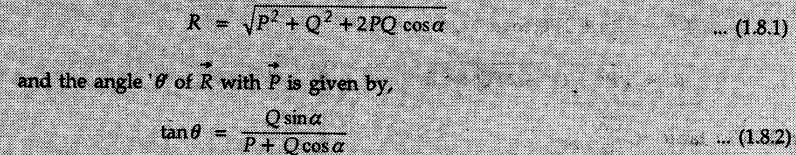
 shown in Fig. 1.8.4 (a) are drawn from a common point A as shown in Fig. 1.8.4 (b). The lengths of AD and AB are proportional to magnitudes of
shown in Fig. 1.8.4 (a) are drawn from a common point A as shown in Fig. 1.8.4 (b). The lengths of AD and AB are proportional to magnitudes of 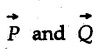 respectively. The parallelogram is completed by drawing lines parallel to AB and AD.
respectively. The parallelogram is completed by drawing lines parallel to AB and AD.![]()

![]() is obtained by measuring the length of diagonal and converting it back to scale. The direction of
is obtained by measuring the length of diagonal and converting it back to scale. The direction of ![]() is obtained by measuring its angle
is obtained by measuring its angle 


![]()
![]() can be obtained using
can be obtained using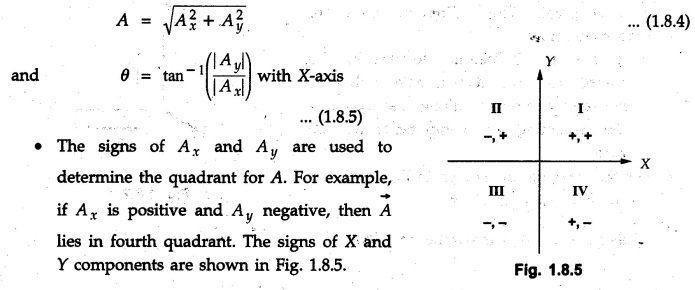

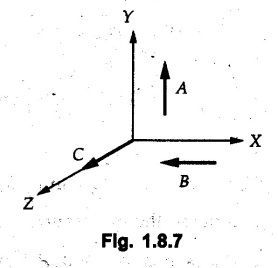
![]() shown in Fig. 1.8.8.
shown in Fig. 1.8.8.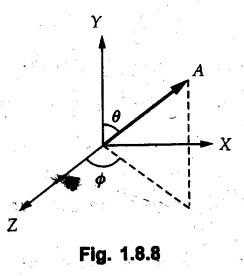
![]() of magnitude 'A' acts from a point B(x1, y1, z1) to C(x2, y2, z2), then
of magnitude 'A' acts from a point B(x1, y1, z1) to C(x2, y2, z2), then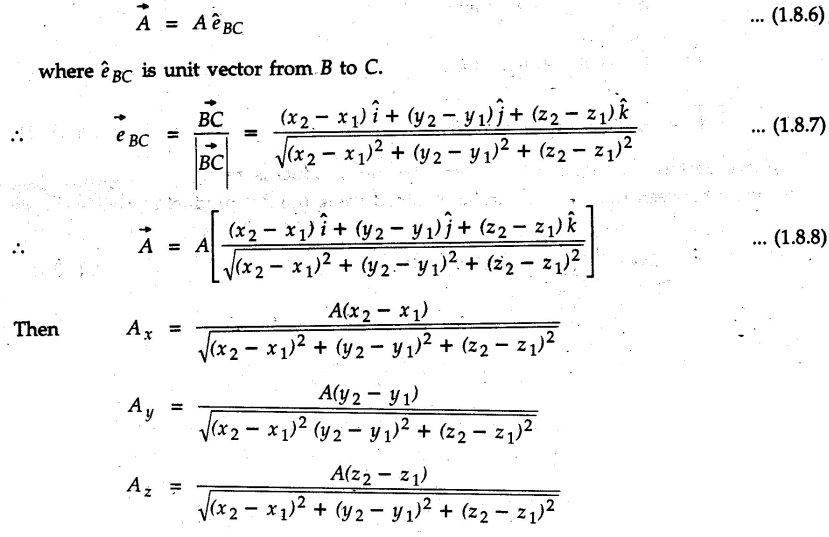
![]() makes angles θx, θy and θz with X, Y and Z axes respectively, then cos θx, cos θy and cos θz (also written as 1, m and n) are called the direction cosines of
makes angles θx, θy and θz with X, Y and Z axes respectively, then cos θx, cos θy and cos θz (also written as 1, m and n) are called the direction cosines of ![]() If the direction cosines are known along with the magnitude 'A', the vector-
If the direction cosines are known along with the magnitude 'A', the vector- ![]() can be written as
can be written as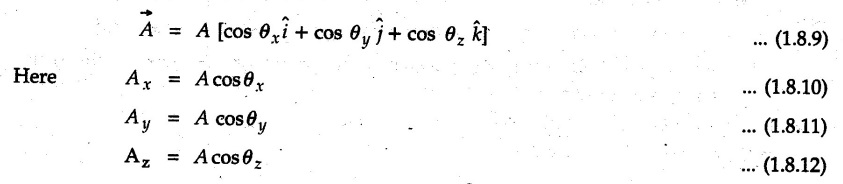
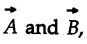 then
then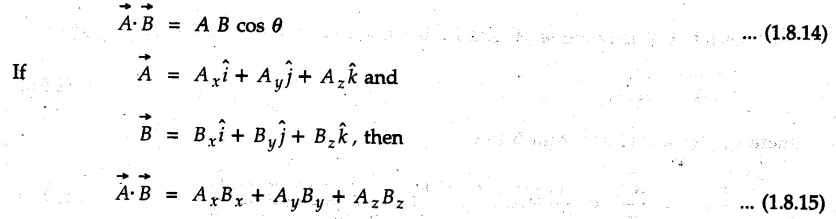

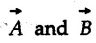 are two vectors then
are two vectors then
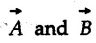 are two vectors then their cross or vector product
are two vectors then their cross or vector product 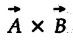 is a vector which has magnitude AB sin θ where θ is angle between
is a vector which has magnitude AB sin θ where θ is angle between 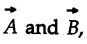 and direction given by right handed screw rule or right hand rule. The direction of
and direction given by right handed screw rule or right hand rule. The direction of 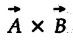 is perpendicular to the plane containing
is perpendicular to the plane containing 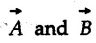 .
.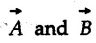 and rotated from
and rotated from 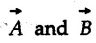 , the direction in which the screw moves of is the direction of
, the direction in which the screw moves of is the direction of 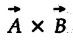 .
.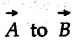 and the thumb is stretched perpendicular to the fingers, then the direction of thumb gives direction of
and the thumb is stretched perpendicular to the fingers, then the direction of thumb gives direction of 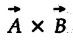 .
.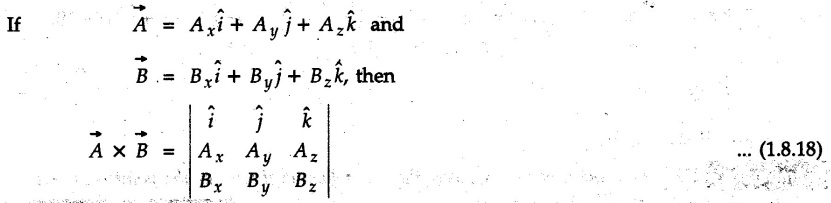
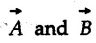 represent adjacent sides of a parallelogram, then
represent adjacent sides of a parallelogram, then 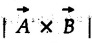 gives the area of parallelogram.
gives the area of parallelogram.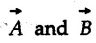 represent sides of a triangle, then area of triangle =
represent sides of a triangle, then area of triangle = 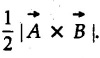
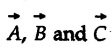 is a scalar given by
is a scalar given by


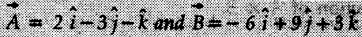 are parallel.
are parallel.

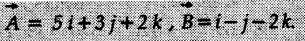
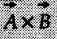 and the unit vector along it.
and the unit vector along it.![]() and the vector resulting from the cross product.
and the vector resulting from the cross product.
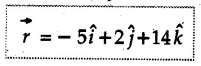



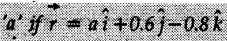 is a unit vector.
is a unit vector.
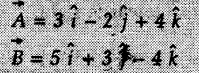

Engineering Mechanics: Unit I: Statics of Particles : Tag: : law, Solved Example Problems - Vector Addition
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
