Two Marks Questions with Answers

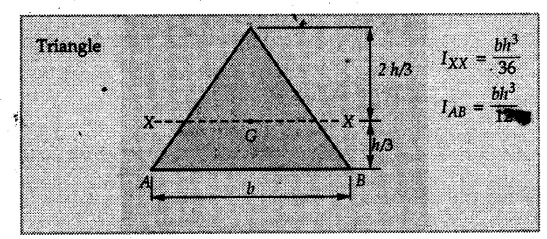
Two Marks Questions with Answers

Q.1

Explain the term 'radius of gyration of an area.

Ans. : 

If an area A shown in Fig. 6.7.1 (a) having moment of inertia I about axis BC is concentrated into a strip of the same area and is placed parallel to BC at distance K as shown in Fig. 6.7.1 (b) such that it has moment of inertia I then K is known as the radius of gyration.

Q.2

Define radius of gyration with respect to X-axis of an area.

Ans. : 

If Ixx = moment of inertia of area A about X-axis,

Q.3

State parallel axes theorem with simple sketch.

Ans. : 

The moment of inertia of any area about an axis in its plane is the sum of moment of inertia about a parallel axis passing through the centroid of the area and the product of area and square of the distance between the two parallel axes.

In Fig. 6.7.2,

IAB = Ixx + Ad2

Q.4

What is the radius of gyration of a circle of diameter d about its diameter?

Ans. : 

The radius of gyration K is given by,

Q.5 

State perpendicular axis theorem. 

Ans. : 

Moment of inertia of an area about an axis perpendicular to its plane (i.e. the polar moment of inertia) at any point is equal to the sum of moments of inertia about any two mutually perpendicular axes through the same point in the plane of the area.

Q.6

Find the radius of gyration of a rectangular area of moment of inertia about its base 9 × 104 cm4 and cross sectional area 300 cm2. 

Ans. : 

I = AK2

A = 300 cm2

I = 9 × 104 cm4

Q.7

What is moment of inertia of traingular lamina (b × h) about its horizontal centroidal axis ?

Ans. : 

Q.8

Using parallel axis thereom find the area moment of inertia of a given area about x-axis.

Ans. : 

For triangle,

Q.9 

Define polar moment of inertia. 

Ans. : 

The moment of inertia of the area about an axis perpendicular to its plane is called as polar moment of inertia.