Engineering Mechanics: Unit III: Distributed Forces
Two Marks Questions with Answers
Centroid | Distributed Forces | Engineering Mechanics
Two Marks Questions with Answers: Distributed Forces - Engineering Mechanics
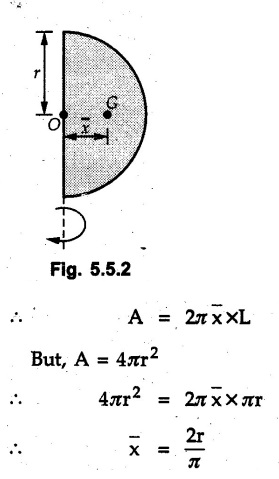
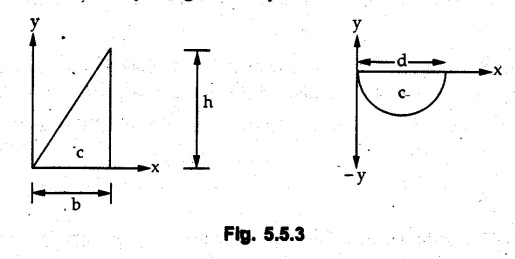
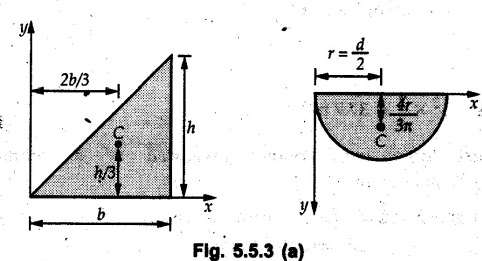
Two Marks Questions with Answers Q.1 Distinguish between centroid and centre of gravity. OR Define centroid. Ans.: Centroid is the geometrical centre of the body whereas centre of gravity is the point through which weight of the body acts. Q.2 Define first moment of an area about an axis. Ans.: The first moment of an area about an axis is the product of area and the perpendicular distance of its centroid from the axis. Q.3 Define line of symmetry. Ans.: Line of symmetry is a line about which the area on one side is a mirror image of the area on the other side. Q.4 What is the position of centroid of a plane lamina with respect to its point of suspension when it is suspended from any point on it? Ans.: The centroid lies on the vertical line passing through the point of suspension. Q.5 State Pappus-Guldinus theorem for finding surface area. Ans.: The area of surface of revolution is equal to the product of length of the generating curve and the distance travelled by the centroid of the generating curve while generating that surface. Q.6 State Pappus-Guldinus theorem for finding volume. Ans.: The volume of a body of revolution is equal to the product of generating area and the distance travelled by centroid of the generating area while generating that volume. Q.7 Use Pappus-Guldinus theorem to find the volume of a sphere of radius r. Ans.: According to Pappus-Guldinus theorem, the volume of body of revolution is product of the generating area and the distance travelled ny centroid of the generating area while generating that body. Sphere is generated by revolving a semicircle about its diameter as shown in Fig. 5.5.1. Q.8 When will the centroid and centre of mass coincides ? Ans.: Centroid and centre of mass coincide when density is uniform throughout the body. Q.9. A right angled triangle of base 3 m and height 4 m is revolved about its 4 m vertical edge. Compute the volume of the solid generated. Ans.: As per Pappus-Guldinus theorem, (Refer Fig. 5.4.3), Distance travelled by the centroid of the generating area Volume generated = Distance travelled by the centroid of generating area × Generating area Q.10. Find surface area and volume generated of a cylinder by using Pappus-Guldinus theorem. Ans.: Surface area generated = Distance travelled by the centroid of generating area × Length of arc ⸫ A = 2лг × h = 2лгh Volume generated = Distance traveled by the centroid of generating area × Generating area V = лг × rh = лr2h Q.11 Find the centroid of a semicircular lamina as shown in Fig. 5.5.2 that is used to generate a sphere by Pappus Guldinus theorem. Ans.: Area of sphere generated = 4лr2 Length of arc = лг Surface area generated = Distance travelled by the centroid of generating area × Length of arc Q.12 Locate the centroid of the given shapes. Ans. :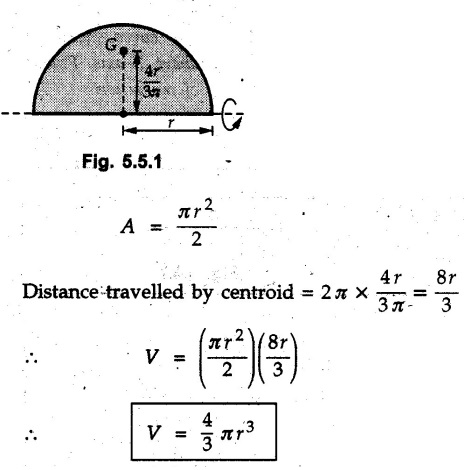
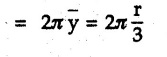

Engineering Mechanics: Unit III: Distributed Forces : Tag: : Centroid | Distributed Forces | Engineering Mechanics - Two Marks Questions with Answers
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
