Engineering Physics: Unit II: Electromagnetic Waves
Two Marks Questions with Answers
Electromagnetic Waves | Engineering Physics
'2' Marks Questions with answers : Engineering Physics: Electromagnetic Waves
Part - 'A' ; '2' Marks Questions with answers 1. Write Maxwell's equation - I from Gauss's law in electrostatics. Integral form Gauss's law in electrostatics states that the total electric flux through any closed surface is equal to the charge enclosed by it. Differential form This is Maxwell's equation from Gauss's law in electrostatics in differential form Statement The total electric displacement through the surface enclosing a volume is equal to the total charge within the volume. 2. Write Maxwell's equation · II from Gauss's law in magnetostatics. Statement The total magnetic flux through any closed surface in a magnetic field is zero ie., This is Maxwell's equation in integral form from Gauss's law in magnetostatics. This is Maxwell's equation in differential form from Gauss's law in magnetostatics. Statement The net magnetic flux 'emerging through any closed surface is zero. 3. Write Maxwell's equation - III from Faraday laws of electromagnetic induction. This is Maxwell's equation in integral form from Faraday's law of electromagnetic induction. This eqn represents Maxwell's equation from Faraday's law of electromagnetic induction in differential form. Statement: The electromotive force around a closed path is equal to the rate of magnetic displacement (flux density) through that closed path. 4. Write Maxwell's equation · IV from Ampere's circuital law. Ampere's law states that the line integral of magnetic field intensity H on any closed path is equal to the current (I) enclosed by that path This is Maxwell's equation in integral form from Ampere's circuital law. The above equations are Maxwell equations in differential form from Ampere's circuital law Statement The magnetomotive force around a closed path is equal to the sum of the conduction current and displacement current enclosed by the path. 5. Give the Maxwell's equations in differential form. 6. Give the Maxwell's equations in integral form. 7. Write the Maxwell's equations for free space. 8. Write the Maxwell's equations for conducting medium. 9. What are the characteristics of Maxwell's First equation • It explains Gauss's law in electrostatics. • It is time independent or steady state equation. • The flux of the lines of electric force depends upon charge density. • Charge acts as a source or sink for the lines of electric force. 10. What are the characteristics of Maxwell's second equation • It expresses a well known observation that isolated magnetic poles do not exist. • It states that total magnetic flux entering and leaving a given volume is equal. • There is no source or sink for lines of magnetic force. • It is a time independent equation. • It explains Gauss's law in Magnetostatics. 11. What are the characteristics of Maxwell's Third equation • It relates the electric field vector • It is a time dependent or time varying equation. • It explains the well known Faraday's laws and Lenz's law of electromagnetic induction. • 12. What are the characteristics of Maxwell's Fourth equation • It gives relation with the magnetic field vector • It is also a time dependent equation. • It explains Ampere's circuital law. • 13. Write the general electromagnetic wave equation in terms of electric field vector μ0 - permeability in free space, ε0 - permittivity in free space. This is general electromagnetic wave equation in terms of electric field vector 14. Write the general electromagnetic wave equation in terms of magnetic field vector μ0 – permeability is free space, ε0 - permittivity is free space. This general electromagnetic wave equation is in terms of 15. Write the expression for velocity of em wave in free space. For vacuum or free space we have μ0 = 4π × 10-7 Hm-1 (henry per metre) and ε0 = 8.842 × 10-12 Fm-1 (farad per metre). 16. Write the general solution of wave equation for plane polarised em wave. Ey = E0 cos (ωt - kx ) and Hz = H0 cos (ωt - kx ) where, ω - angular frequency k - wave vector 17. Write the relation between the electric field vector This is the relation between the electric field vector and magnetic field vector. It is determined by the μ0 and ε0 18. What is intrinsic or characteristic impedance of free space? The ratio ie., ohm, Therefore, the quantity It is known as intrinsic or characteristic impedance of free space, denoted by Z0. It is a constant quantity for free space and having value = 377Ω. 19. What is poynting vector? The cross product of electric field vector 20. Write the general wave equation for the electric vector in an em wave in conducting medium. μ– permeability of medium. ε - permittivity of medium. This is the general wave equation for the electric vector in an electromagnetic wave propagating in conducting medium. 21. Write the general wave equation for the magnetic vector in an em wave in conducting medium. In a similar way, by taking the curl of the eqn. (4) we obtain the general wave equation for the magnetic vector in a conducting medium as μ – permeabity of medium. ε - permittivity of medium. 22. What is skin depth? It is defined as the distance inside the conductor from the surface of the conductor at which the amplitude of the field vector is reduced to 1le times its value at the surface. 23. Define intensity of EM wave. The magnitude of the average value of ε0 - permittivity of the medium. c - velocity of light. 24. Define radiation pressure. The force per unit area on an object due to EM radiation is the radiation pressure Pr, 25. Give the Properties of Electromagnetic Waves. (i) Electromagnetic waves are produced by accelerated charges. (ii) They do not require any material medium for propagation. (iii) In an electromagnetic wave, the electric (iv) Variation of maxima and minima in both (v) They travel in vacuum or free space with a speed 3 × 108 ms-1 given by the relation (μ0 - permeability of free space and ε0 - permittivity of free space) (vi) The energy in an electromagnetic wave is equally divided between electric and magnetic field vectors. (vii) The electromagnetic waves being chargeless, they are not deflected by electric and magnetic fields.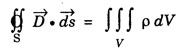
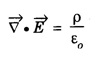
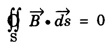
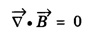
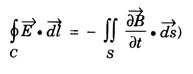
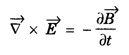
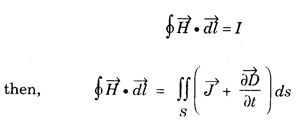
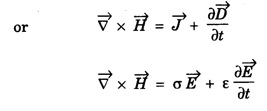
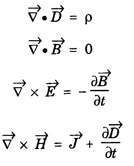
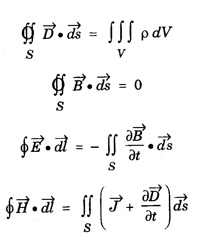
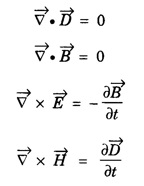
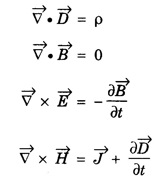
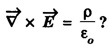
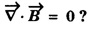
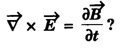
![]() and magnetic induction vector
and magnetic induction vector ![]()
![]() is generated by the time variation of
is generated by the time variation of ![]()
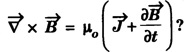
![]() with displacement vector
with displacement vector ![]() and the current density
and the current density ![]()
![]() can be produced by
can be produced by ![]() and the time variation of
and the time variation of ![]()
![]() for free space.
for free space.
![]() for free space.
for free space.![]() for free space.
for free space.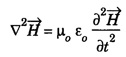
![]() for free space.
for free space. 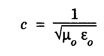
![]() and magnetic field vector
and magnetic field vector ![]()

![]() is having the unit of impedance (Resistance)
is having the unit of impedance (Resistance)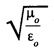 has the dimensions of impedance.
has the dimensions of impedance.![]() and the magnetic field vector
and the magnetic field vector ![]() is called poynting vector. It is denoted by
is called poynting vector. It is denoted by 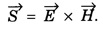
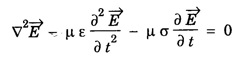
![]() - electric field vector.
- electric field vector.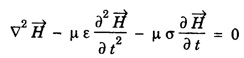
![]() - Magnetic field vector.
- Magnetic field vector. ![]() at a point is called the intensity of radiation at that point. The S.I unit of intensity is W/m2. It is given by
at a point is called the intensity of radiation at that point. The S.I unit of intensity is W/m2. It is given by

![]() and magnetic
and magnetic ![]() field vectors are at right angles to each other and to the direction of propagation. Hence, electromagnetic waves are transverse in nature.
field vectors are at right angles to each other and to the direction of propagation. Hence, electromagnetic waves are transverse in nature.  occur simultaneously (in phase).
occur simultaneously (in phase). 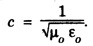
Engineering Physics: Unit II: Electromagnetic Waves : Tag: : Electromagnetic Waves | Engineering Physics - Two Marks Questions with Answers
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
