Strength of Materials: Unit V: Thin Cylinders, Spheres and Thick Cylinders
thick cylinders and thick spherical shells
Thin Cylinders, Spheres and Thick Cylinders - Strength of Materials
The ratio of thickness (t) to internal diameter (d) of a cylindrical shell is less than about 1/20, then the cylindrical shell is known as thin cylinders. For thin cylinders the hoop stress and longitudinal stresses are constant over thickness.
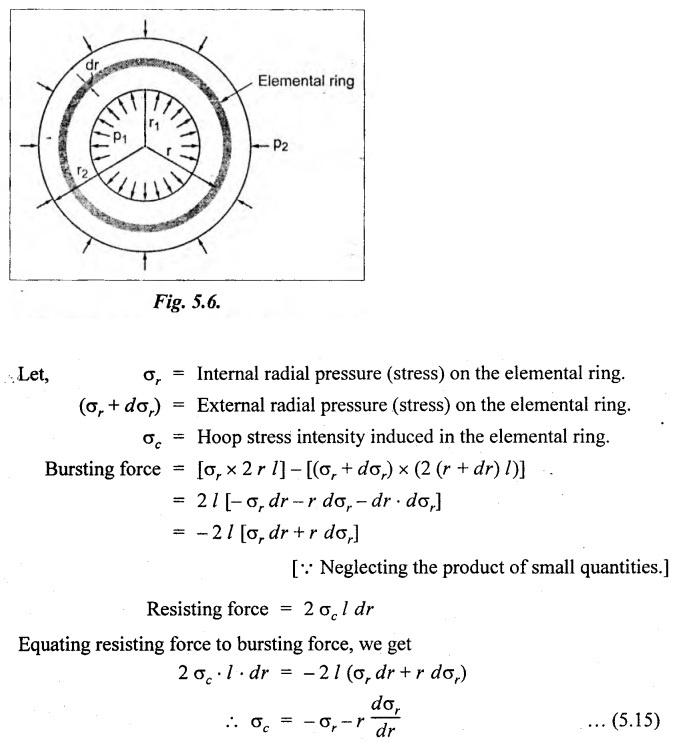
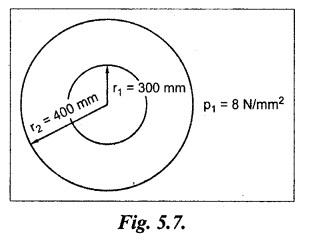
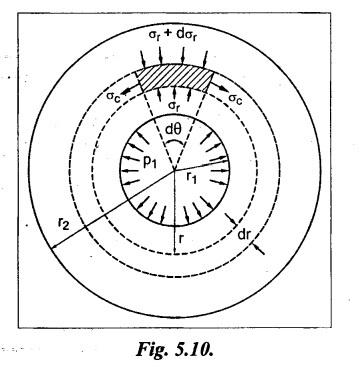
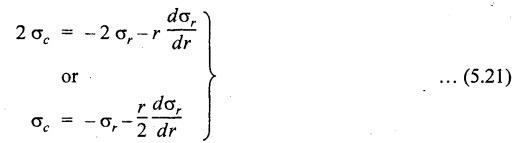
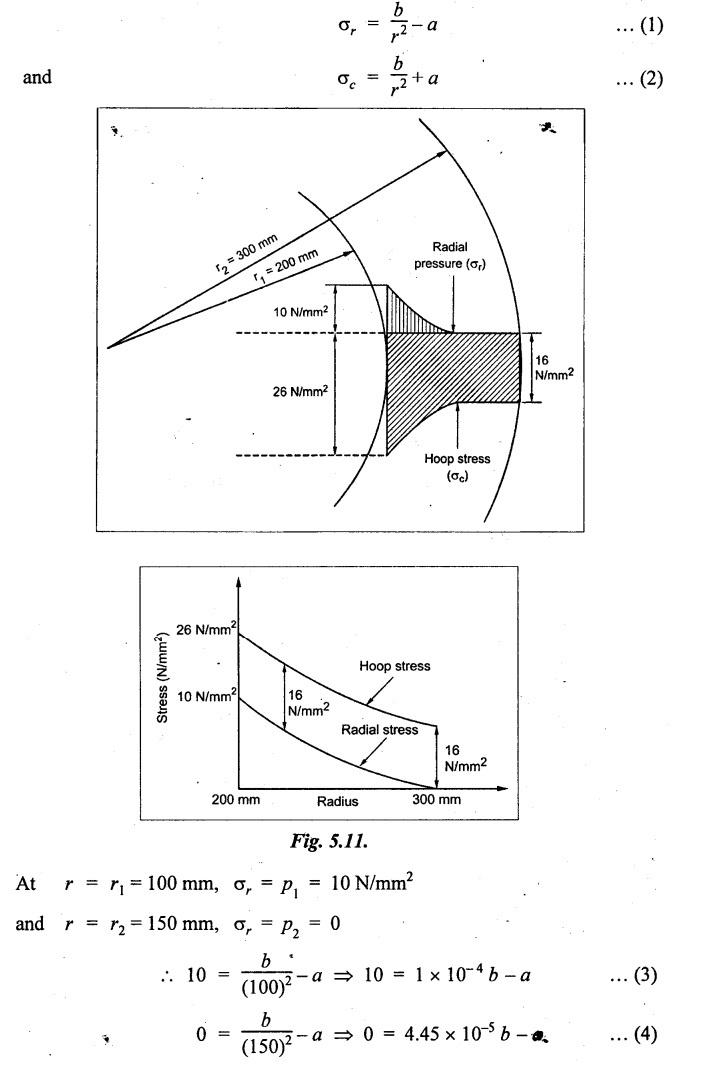
THICK CYLINDERS AND THICK SPHERICAL SHELLS The ratio of thickness (t) to internal diameter (d) of a cylindrical shell is less than about 1/20, then the cylindrical shell is known as thin cylinders. For thin cylinders the hoop stress and longitudinal stresses are constant over thickness. The ratio of thickness (t) to internal diameter (d) of a cylindrical shell is more than 1/20, then the cylindrical shell is known as thick cylinders. The hoop stress in the thick cylinder will not be uniform across thickness. Actually the hoop stress will vary from a maximum value at the inner circumference to a minimum value at the outer circumference. The variation in the radial as well as circumferential stress across the thickness are obtained with the help of Lame's theory. The assumptions made in Lame's theory are as follows: 1. The material is homogeneous and isotropic. 2. The material is stressed within elastic limit. 3. Plane section perpendicular to the longitudinal axis of the cylinder remain plane after the application of internal pressure. 4. All the fibres of the material are to expand or contract independently without being constrained by the adjacent fibres. Fig.5.6 shows that the thick cylinder subjected to internal and external radial pressure. Let, r1 = Internal radius of the thick cylinder r2 = External radius of the thick cylinder p1 = Pressure on the inner surface of the cylinder p2 = Pressure on the outer surface of the cylinder The thickness of thick cylinder may be taken to consists of a number of concentric element rings. Consider one such elemental ring of radius 'r' and thickness 'dr'. Now we will obtain another relation between the radial pressure and hoop stress by using the condition that the longitudinal strain at any point in the section is the same Hence at any point in the section of the elemental ring considered above, the following three principal stresses exist: (i) The radial pressure (σr) (ii) The hoop stress or circumferential stress (σc) (iii) The longitudinal tensile stress (σl) Since the longitudinal strain (e1) is constant, we have Integrating both sides, we get The constants a and b can be evaluated from the known internal and external radial pressure and radius. The equation (5.18) and (5.19) are called Lame's equation. Longitudinal Stress Shear Stress The maximum shear stress is given by, Example 5.27 A pipe of 600 mm internal diameter and 800 mm external diameter contains a fluid pressure of 8 N/mm2. Find the minimum and maximum hoop stress across the section. Also, sketch the radial pressure distribution and hoop stress distribution across the section. Given: To find: 1. To find the maximum and minimum hoop stress circumferential stress (σc). 2. To draw the radial and hoop stress distribution Solution: We know that the Lame's equations, Equation (3) and (4) becomes Substituting values of a and b in equation (2), Result: 1. Maximum hoop stress, σc = 28.58 N/mm2 2. Minimum hoop stress, σc = 20.58 N/mm2 Example 5.28 Find the thickness of metal necessary for a cylindrical shell of internal diameter 150 mm to withstand an internal pressure of 25 N/mm2. The maximum hoop stress in the section is not to exceed 125 N/mm2. Given: To find: Thickness of the metal (t) Solution: Substituting in equation (1) and (2), we get Equation (3) and (4) becomes, Solving equation (5) and (6), we get Result: Thickness of metal (t) = 17 mm Example 5.29 A steel cylinder of 1200 mm inside diameter is to be designed for an internal pressure of 5 N/mm2. Calculate (a) The thickness if the maximum shearing stress is not to exceed 20 N/mm2. (b) The increase in volume, due to working pressure if the cylinder is 7 m long with closed ends. Neglect any constraints due to ends. Take E = 200 × 103 N/mm2. Poisson's ratio = 0.33. Given: To find: Solution: (a) Wall thickness: The Lame's equations are, Absolute maximum shearing stress will act on the internal surface, (b) Increase in volume, δv: Result: 1. Thickness of wall, t = 93.8 mm 2. Increase in volume (δv) = 2.7 × 106 mm3 In case of think cylinders that when a thin cylinder is wound with wire under tension, the whole shell will be in a state of initial compression; but when fluid is admitted, the circumferential stress is reduced. This method can also be used in case of thick cylinders to reduce the maximum circumferential stress. Another method is to shrink one cylinder over the other. Due to this, the inner cylinder will be put into initial compression whereas the outer cylinder will be put into initial tension. If now the compound cylinder is subjected to internal fluid pressure, both the inner and outer cylinders will be subjected to hoop tensile stress. The net effect of the initial stresses due to shrinking and those due to internal fluid pressure is to make the resultant stresses more or less uniform. Fig.5.9 shows a compound thick cylinder made up of two cylinders. Let r1 = Inner radius of compound cylinder r3 = Outer radius of compound cylinder r2 = Radius at the junction Initial Stresses: Let p = The shrinkage pressure r2 = Radius at the common surface Inner tube: Inner radius = r1, Outer radius = r2 Outer tube: Inner radius = r2, Outer radius = r3 Stresses due to fluid pressure: In the compound cylinder, when the fluid is admitted, the intensity of pressure is resisted jointly by the section. By applying Lame's equations to the compound cylinder (under initial pressure). At r = r, σr = p r = r3, σr = 0 Final stresses: Example 5.30 A compound cylinder, A compound cylinder, formed by shrinking one tube to another is subjected to an internal pressure of 80 N/mm2. Before the fluid is admitted, the internal and external diameters of the compound cylinder are 200 mm and 300 mm respectively and the diameter at the junction is 240 mm. If after shrinking on the radial pressure at the common surface is 8 N/mm2, determine the final stresses developed in the compound cylinder. Given: To find: Final stresses in the compound cylinder Solution: Lame's equations: (a) Before the fluid is admitted: By solving equations (5) and (6), we get b = -258065 and a = -25.8 Hence circumferential stress at any point in the inner tube will be given by, Negative sign indicates wholly compressive, Outer tube: At r = r3 = 150 mm, σr = 0 At r = r2 = 120 mm, σr = 8 N/mm2 By solving equation (7) and (8), we get Positive sign indicates wholly tensile, (b) After the fluid is admitted: By solving equations (9) and (10), we get b = 1438850 and a = 64 Hence hoop stress at any point in the compound tube is given by Result: The final circumferential or hoop stresses are: Inner tube: (σc)100 = 156.2 N/mm2 (tensile) (σc)120 = 120.2 N/mm2 (tensile) Outer tube: (σc)120 = 192.2 N/mm2 (tensile) (σc)150 = 164.2 N/mm2 (tensile) Fig.5.10 shows a thick spherical shell. Let r1= Inner radius; r2 = Outer radius; p = Internal fluid pressure Consider an elemental disc of the spherical shell at a radius r, having thickness dr. Let this elemental part subtend an angle do at the centre. σ + d σr = Radial compressive stress at radius (r + dr) Let us consider the forces on a elementary spherical shell of radius r and thickness dr, to form equation between the principal stresses σr and σa. The bursting force on any diameteral plane on the section of the elemental shell Equating the resisting force and the bursting force, we get Neglecting squares and products of very small quantities, then At any point at radius 'r', the principal stresses are, (i) The radial stress (pressure) σr [compressive] (ii) The circumferential stress, σc [tensile] (iii) The circumferential stress σcʹ = σc [tensile] on a plane at right angles. Differentiating the equation (5.21), we get The above strains are tensile if positive. From equation (5.25) and (5.26), we have Simplifying and rearranging, we have On simplification, we get Integrating both sides, we get Integrating both sides, we get Now, let us consider the two expression for σr and σc, Applying the given conditions, we get Solving equation (5.32) and (5.33), we get Example 5.31 A thick spherical shell of 200 mm internal diameter is subjected to an internal fluid pressure of 20 N/mm2. If the permissible stress is 100 N/mm2, find the thickness of the shell. Given: To find: Thickness of spherical shell (t) Solution: We know that, for thick spherical shell Solving equation (3) and (4), we get Result: Thickness of shell, t = 10 mm Example 5.32 A pipe of 200 mm internal diameter and 50 mm thickness carries a fluid at a pressure of 10 MN/m2. Calculate the maximum and minimum intensities of circumferential stresses across the section. Also sketch the radial pressure and circumferential stress distribution across the section. Given: To find: 1. Maximum and minimum hoop stresses 2. Sketch of radial and hoop stresses Solution: The Lame's equations are, By solving equations (3) and (4), we get1. INTRODUCTION
2. ASSUMPTIONS OF LAME'S THEORY
3. STRESSES IN THICK CYLINDER
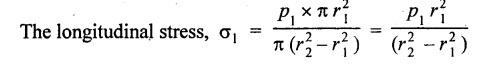
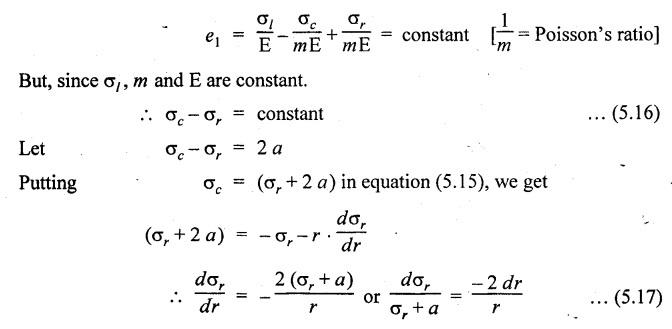
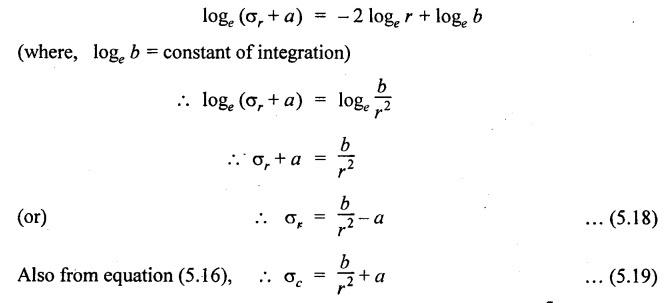


4. FORMULAE USED IN THICK CYLINDER

5. SOLVED PROBLEMS




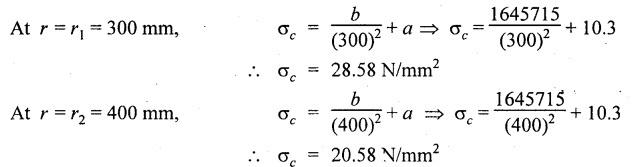

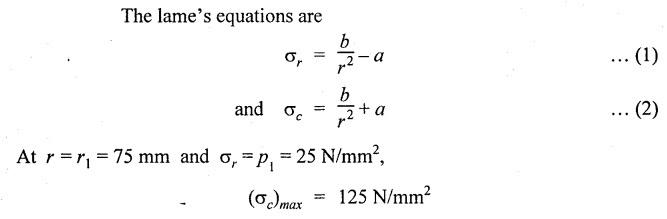
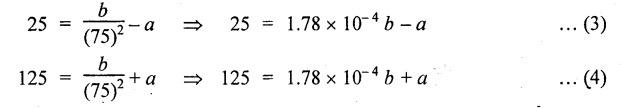



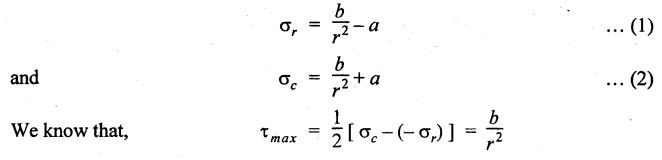


6. COMPOUND (OR) SHRUNK CYLINDERS

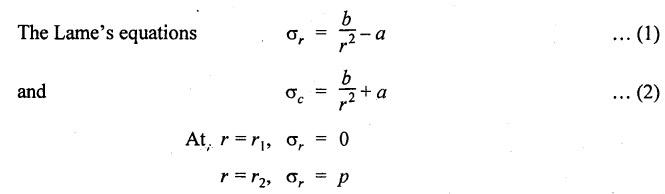


7. SOLVED PROBLEMS

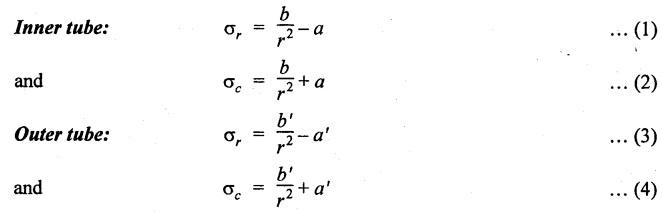

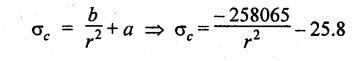
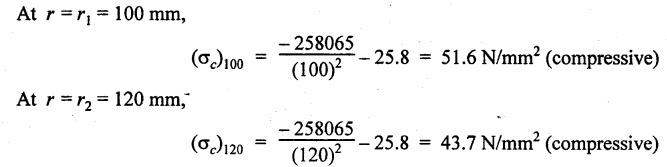
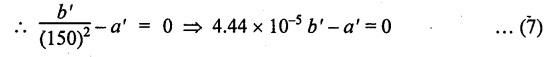
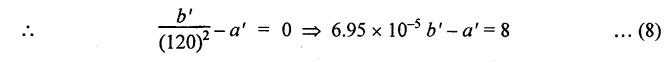
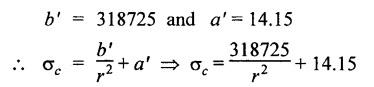



8. THICK SPHERICAL SHELLS

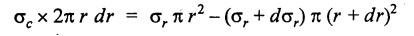
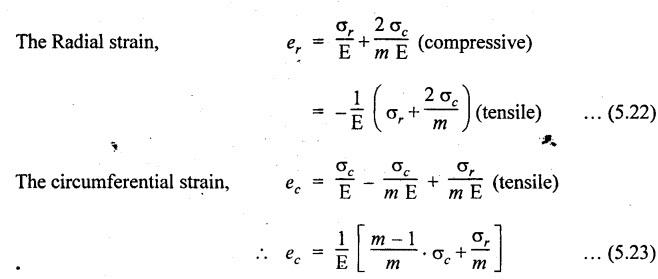

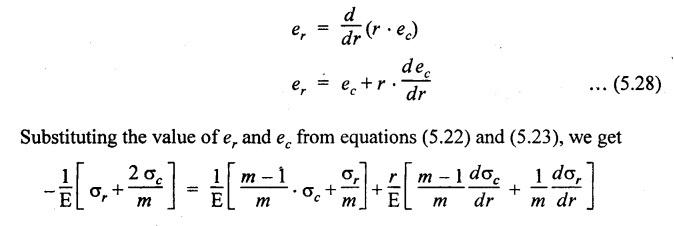

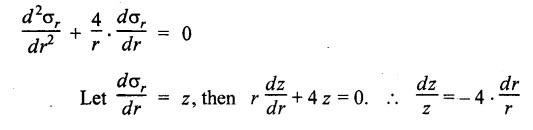
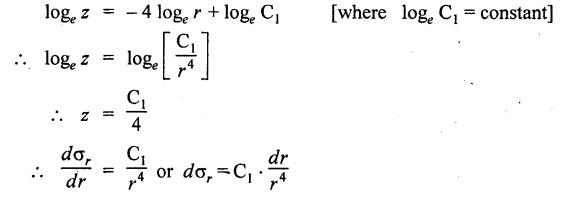

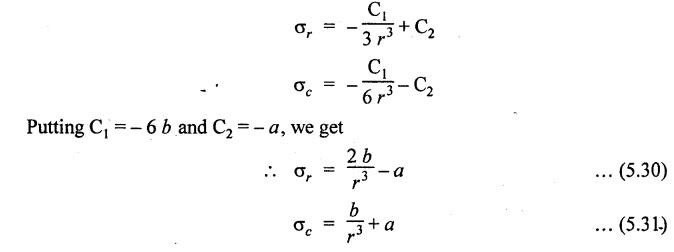

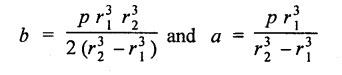
9. SOLVED PROBLEMS
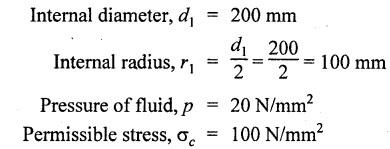


10. ANNA UNIVERSITY SOLVED PROBLEMS

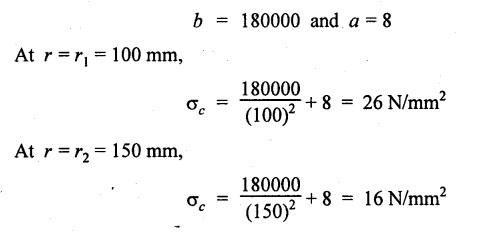
Strength of Materials: Unit V: Thin Cylinders, Spheres and Thick Cylinders : Tag: : Thin Cylinders, Spheres and Thick Cylinders - Strength of Materials - thick cylinders and thick spherical shells
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
