Strength of Materials: Unit V: Thin Cylinders, Spheres and Thick Cylinders
solved university problems
Thin Cylinders, Spheres and Thick Cylinders - Strength of Materials
solved university problems: Strength of Materials: Unit V: Thin Cylinders, Spheres and Thick Cylinders
SOLVED UNIVERSITY PROBLEMS Example 5.21 A spherical shell of 80 mm diameter has to withstand an internal pressure of 280 N/cm2. Calculate the thickness of the shell wall if the maximum permissible stress is 30 N/mm2. Note: Same as Example 5.14. Ans: t = 1.867 mm Example 5.22 An cylindrical shell 1 m diameter and 3 m length is subjected to an internal pressure of 2 MPa. Calculate the minimum thickness if the stress should not exceed 50 MPa. Find the change in diameter and volume of the shell. Poisson's ratio 0.3 and E = 200 kN/mm2. Given: Solution: Results: Thickness of cylinder, t = 20 mm Change in diameter, δ d = 0.2125 mm Change in volume, δ v = 1119195 mm3 Example 5.23 A spherical shell of internal diameter 1 m and thickness of 10 mm is subjected to an internal pressure of 1.5 MPa. Determine the increase in diameter and volume, E = 200 kN/mm2. Poisson's ratio is 0.3. Note: Same as Example 5.15. Ans: Change in diameter, δ d = 0.13125 mm Change in volume, δ v = 206167 mm3 Example 5.24 A cylindrical shell 3 m long, 1 m in diameter and 10 mm thick is subjected to an internal pressure of 2 MPa. Calculate the change in dimensions of the shell. E = 2 × 105 MPa. Poisson's ratio = 0.3. Note: Same as Example 5.6. Ans: (i) Change in diameter, δ d = 425 mm (ii) Change in length, δ l = 0.3 mm (iii) Change in volume, δ v = 2.2384 × 106 mm3 Example 5.25 A thin spherical shell of 2 m diameter and of thickness 10 mm is filled with an incompressible liquid. Estimate the quantity of liquid that should be pumped in so as to raise the pressure to 5 N/mm2. Take E 200 kN/mm2 and μ = 0.3. Given: Diameter of spherical shell, d = 2 m = 2000 mm Thickness of spherical shell, t = 10 mm Pressure of liquid, p = 5 N/mm2 Young's modulus, E = 200 kN/mm2 = 2 × 105 N/mm2 Poisson's ratio, μ = 1/m = 0.3 Solution: Amount of liquid to be pumped to raise the pressure to 5 N/mm2. Amount of liquid to be pumped = Change in volume of cylinder. Result: Amount of liquid to be pumped, δv = 10.99 × 106 mm3 Example 5.26 A cylindrical shell 3 m long, 1 m internal diameter and 10 mm thick is subjected to an internal pressure of 1.5 N/mm2. Calculate the changes in length, diameter and volume of the cylinder. E 200 kN/mm2, poisson's ratio = 0.3. Note: Same as Example 5.6. Ans: (i) Change in length, δl = 0.322 mm (ii) Change in diameter, δd = 0.31875 mm (iii) Change in volume, δ v = 1678788.57 mm3

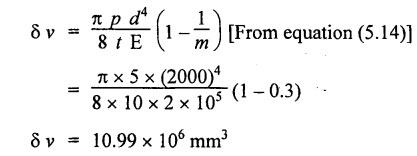
Strength of Materials: Unit V: Thin Cylinders, Spheres and Thick Cylinders : Tag: : Thin Cylinders, Spheres and Thick Cylinders - Strength of Materials - solved university problems
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
