Strength of Materials: Unit V: Thin Cylinders, Spheres and Thick Cylinders
solved problems on thin cylinders and shells
Thin Cylinders, Spheres and Thick Cylinders - Strength of Materials
solved problems on thin cylinders and shells: Strength of Materials: Unit V: Thin Cylinders, Spheres and Thick Cylinders
SOLVED PROBLEMS ON THIN CYLINDERS AND SHELLS Example 5.1 A mild steel pipe of diameter 1.3 m and thickness 12 mm is subjected to an internal fluid pressure of 1 N/mm2. Calculate the hoop stress and longitudinal stress developed in the pipe. Given: Diameter of pipe, d = 1.3 m = 1300 mm Thickness of pipe, t = 12 mm Internal pressure, p = 1 N/mm2 Solution: Hoop stress developed in the pipe, Longitudinal stress developed in the pipe, Result: Example 5.2 A thin cylinder of 1 m diameter is required to convey water under a head of 120 m. Determine the thickness of the cylinder, if the allowable stress in the pipe material is 90 N/mm2. Given: Solution: Pressure due to 120 m head of water, Maximum or allowable stress in the pipe material means the circumferential stress, Result: Thickness of the cylinder, t = 6.6mm Example 5.3 A cylinder air receiver for a compressor has an internal diameter of 2 m and thickness of 15 mm. If the tensile stress in the material is not to exceed 85 N/mm2, determine the maximum safe air pressure. Given: Diameter of cylinder, d = 2 m = 2000 mm Thickness of cylinder, t = 15 mm Tensile stress in the material, Solution: Result: Maximum safe air pressure, p = 1.275 N/mm2. Example 5.4 The shell of a boiler is 2.25 m in diameter and made of 15 mm thick plates. If the hoop and longitudinal stresses in the material are not to exceed 95 N/mm2 and 58 N/mm2 respectively, find the maximum allowable pressure of the steam inside the boiler. Given: Solution: From the above two values of pressure, take the minimum pressure as a allowable pressure, since it is the limiting pressure. Result: The maximum allowable pressure of steam inside the boiler shell is 1.2667 N/mm2. Example 5.5 A thin cylindrical pipe of internal diameter 1.5 m contains a fluid at a pressure of 1.87 N/mm2. Determine the thickness of the pipe wall if the hoop and longitudinal stresses in the pipe material are not to exceed 60 N/mm2 and 46 N/mm2 respectively. Given: Solution: From the above two values of t, we should take 23.375 mm as the minimum take thickness of the pipe wall. If we take 15.24 mm, the pipe will burst due to circumferential stress. Result: Example 5.6 A hollow cylindrical drum 750 mm in diameter and 2.5 m long has a shell thickness of 10 mm. If the drum is subjected to an internal pressure of 2.6 N/mm2 Determine (i) Change in diameter (ii) Change in length and (iii) Change in volume. Take E = 2.1 × 105 N/mm2 and Poisson's ratio = 0.3. Given: Diameter of cylinder, d = 750 mm Length of cylinder, I = 2.5 m = 2500 mm Thickness of cylinder, t = 10 mm Internal pressure, p = 2.6 N/mm2 Young's modulus, E = 2.1 × 105 N/mm2 Poisson's ratio, 1/m = 0.3 Solution: (i) Change in diameter: We know that, (ii) Change in length: (iii) Change in Volume: Result: (i)Change in diameter, δ d = 0.296 mm (ii) Change in length, δl = 0.232 mm (iii) Change in volume, δv = 973885.71 mm3 Example 5.7 A cylindrical shell of 1 m long, 150 mm internal diameter having thickness of metal as 7 mm is filled with fluid at atmosphere pressure. If an additional 25 cc of fluid is pumped into the cylinder, find the pressure exerted by the fluid on the cylindrical shell and the resulting hoop stress. Assume E = 2 × 105 N/mm2 and Poisson's ratio = 0.27. Given: Length of shell, l = 1 m = 1000 mm Diameter of shell, d = 150 mm Thickness of shell, t = 7 mm Solution: Result: Pressure on the cylindrical shell, p = 13.47 N/mm2 Example 5.8 A closed cylindrical drum 600 mm in diameter and 2 m long has a shell thickness of 12 mm. If it carries a fluid under a pressure of 3 N/mm2, calculate the longitudinal and hoop stress in the drum wall and also determine the change in diameter, change in length and change in volume of the drum Take E=200 GPa and 1 / m = 0.3. Given: Solution: Result: Example 5.9 A thin cylindrical shell 400 mm in diameter has shell thickness of 6 mm subjected to an internal pressure which produces a strain of 2000 diameter. Calculate the internal pressure and corresponding hoop and longitudinal stresses. Take E = 2.1 x 10 N/mm2 and 1/m = 0.26. Given: Solution: Result: Internal pressure, p = 3.62 N/mm2 Hoop stress, σc = 120.69 N/mm2 Longitudinal stress, σa = 60.34 N/mm2 Example 5.10 A thin cylindrical shell 3 m long, 1.2 m in diameter is subjected to an internal pressure of 1.67 N/mm2. If the thickness of the shell is 13 mm, find the circumferential and longitudinal stresses. Also find the maximum shear stress and change in dimensions of the shell. Assume E = 2 × 105 N/mm2 and 1/m = 0.28. Given: Length of shell, l = 3 m = 3000 mm Diameter of shell, d = 1200 mm Internal pressure, p = 1.67 N/mm2 Thickness of shell, t = 13 mm Young's modulus, E = 2 × 105N/mm2 Poisson's ratio, 1 / m = 0.28 Solution: We know that, We know that, We know that, Note: The same problem can also be solved in a similar manner as that of problem 5.8. Result: Example 5.11 A steel cylindrical pipe with closed ends is 75 mm internal diameter and 3 mm thick. The pipe is axially loaded in tension with a load of 12 kN and is subjected to an axial torque of 2 × 106 N-mm under an internal pressure of 5.5 N/mm2. Determine the principal stresses and maximum shear stress on the pipe. Given: Solution: Longitudinal stress will be produced by means of internal pressure as well as axial load. Longitudinal stress due to pressure, Longitudinal stress due to axial load, Cross sectional area of the pipe, Shear stress will be produced in the tube due to the torque. Maximum principal stress, Minimum principal stress, Result: Example 5.12 A steel cylinder is made of 12 mm thick plate has 2 m long and 1.2 m diameter. It is filled with water until the pressure is 2.5 N/mm2. On relieving the pressure, the water outlet measured 50 × 105 mm3. Calculate the bulk modulus of water if E for steel is 2 × 105 N/mm2 and Poisson's ratio is 0.3. Given: Thickness of cylinder, t = 12 mm Length of cylinder, l = 2 m = 2000 mm Diameter of cylinder, d = 1.2 m = 1200 mm Pressure of water, p = 2.5 N/mm2 Volume of water relieved, v = 50 × 105 N / mm3 Young's modulus, E = 2 × 105 N /mm2 Poisson's ratio, 1/ m = 0.3 Solution: For water under pressure: Result: Bulk modulus of water, K = 2443.8 N/mm2 Example 5.13 A thin spherical vessel of 1.5 m internal diameter and 15 mm shell thickness is completely filled with a fluid at 1.75 N/mm2. Determine the stress induced in the material of the vessel. Given: Diameter of vessel, d = 1.5 m = 1500 mm Thickness of vessel, t = 15 mm Pressure of fluid, p = 1.75 N/mm2 Solution: Stress induced in the material, Result: Stress induced in the material, σ = 43.75 N/mm2 Example 5.14 A vessel in the shape of a spherical shell 600 mm in diameter is subjected to an internal pressure of 1.2 N/mm2. Find the thickness of the plate required if maximum stress is not to exceed 72 N/mm2. Given: Diameter of spherical shell, d = 600 mm Internal pressure, p = 1.2 N/mm2 Maximum stress, σc = 72 N/mm2 Solution: Result: Thickness of the plate required, t = 2.5 mm Example 5.15 A thin spherical shell 750 mm diameter and 8 mm thick is filled with water at 1.8 N/mm2. Determine the change in dimensions of the spherical shell. Take E- 2 × 105 N/mm2 and 1 / m = 0.3. Given: Diameter of spherical shell, d = 750 mm Thickness of spherical shell, t = 8 mm Pressure of water, p = 1.8 N/mm2 Young's modulus, E = 2 × 105 N/mm2 Poisson's ratio, 1 / m = 0.3 Solution: Result: Change in diameter, δd = 0.1107 mm Change in volume, δ v = 97848.8 mm3 Example 5.16 A spherical vessel 250 mm in diameter, with a wall thickness 6 mm, is full of water at atmosphere pressure. If an additional 7500 mm3 of fluid is pumped into the cylinder, find the pressure exerted by the fluid on the wall of the sphere. Take E = 2.1 × 105 N/mm2 and 1 / m = 0.3 Given: Diameter of vessel, d = 250 mm Thickness of vessel, t = 6 mm Additional liquid pumped, δv = 7500 mm3 Young's modulus, E = 2.1 × 105 N/mm2 Poisson's ratio, = 1 / m = 0.28 Solution: Result: Pressure exerted by the fluid, p = 8.556 N/mm2 Example 5.17 A spherical shell is made of 12 mm thick steel plate and has an internal diameter of 1.25 m. It is filled with oil at a pressure of 3 MPa. Owing to a leakage, oil escapes until the pressure falls to 1.5 MPa. Calculate the volume of oil that has escaped and also the change in the internal diameter of shell due to this leakage. Bulk modulus of oil is 2.8 GPa. Take E = 200 GPa and 1/m = 0.3. Given: Diameter of spherical shell, d = 1.25 m = 1250 mm Thickness of spherical shell, t = 12 mm Initial oil pressure, P1= 3 MPa = 3 N/mm2 Final oil pressure, p2 = 1.5 MPa = 1.5 N / mm2 Bulk modulus, K = 2.8 GPa = 2.8×103 N/mm2 Young's modulus, E = 200 GPa = 2 x 105 N / mm2 Poisson’s ratio, 1 / m = 0.3 Solution: At 3 MPa: Change in volume of the shell due to internal pressure of 3 MPa. At 1.5 MPa: Change in volume of the shell due to 1.5 MPa. Result: Example 5.18 A thin spherical vessel 1.5 m in diameter and made of 10 mm thick steel is first filled with water at atmospheric pressure. What additional volume of water must be pumped into the vessel to raise the internal water pressure 0.3. to 1.5 MPa? Take E = 2 × 105 N/mm2, K = 2.2 GPa, 1/m – 0.3. Given: Solution: Change in volume of the shell due to 1.5 MPa pressure Change in volume of water due to 1.5 MPa pressure Result: Additional volume of water pumped = 2.2486 × 106 mm3 Example 5.19 A vessel in the shape of a spherical shell of 1.2 m internal diameter and 10 mm thickness is filled with a fluid at atmospheric pressure. If additional 500 c.c, of fluid is pumped into the shell at atmospheric pressure, find the internal pressure exerted on the wall of the shell. Find also the resulting change in volume of sphere. Take E = 2.1 × 105 N/mm2, 1/m – 0.28 and K for fluid as 2.4 GPa. Given: Solution: Change in volume of fluid due to pressure Result: Pressure exerted, p = 0.76 N/mm2 Change in volume, δ v = 212183.526 mm3 Example 5.20 A cast iron pipe 300 mm in diameter, 10 mm length and 10 mm thick is closely wound with one layer of 5 mm steel wire under a tension of 40 N/mm2. Calculate the radial stress which may be exerted on the inside wall of the pipe if the stress in the pipe section due to water pressure is 8 N/mm2. Calculate also the stress in the steel wire. Take E for steel 2 × 105 N/mm2 and E for cast iron = 1 × 105 N/mm2. Poisson's ratio = 0.3. Given: Solution: Before water is admitted under pressure in the pipe: It will be under compression due to tension of wound wire. Number of turns of wire in 10 mm length The compressive force exerted by two turns of the wire on the pipe is given by, 2 × 2 are for two cross sections of wires on each side of the pipe. Therefore the stresses in the pipe and wire before the water is admitted is In the pipe = 15.7 N/mm2 In the wire = 40 N/mm2 When the water pressure of 8 N/mm2 is introduced: Let, σp - Stress in the pipe due to water pressure alone σw - Stress in the wire due to water pressure alone The bursting force of fluid per 10 mm length of pipe = p × dl = 8 × 300 × 10 = 24000 N The bursting force is resisted by the wire as well as pipe The resisting force of wire The resisting force of pipe Equating the resisting force to the bursting force We know that, the circumferential strain in the pipe and wire must be the same. Equating the strain wire and pipe Resultant stresses in pipe and wire: Result: Resultant stress in wire = 154.26 N/mm2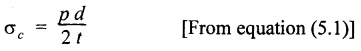

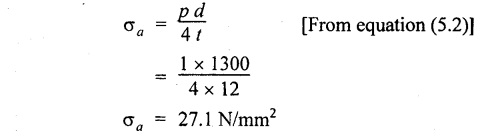
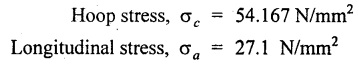

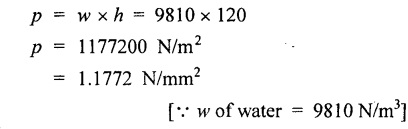
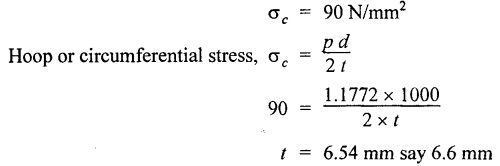
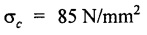
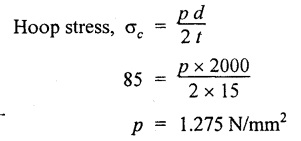


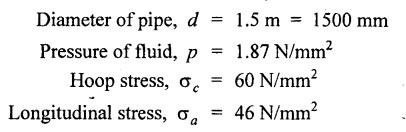



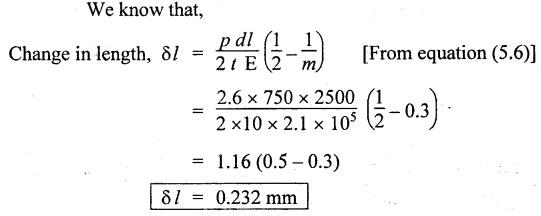












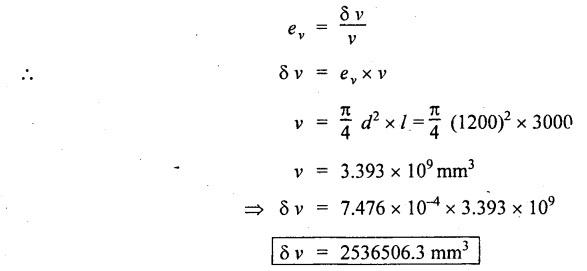



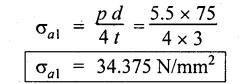
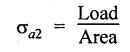
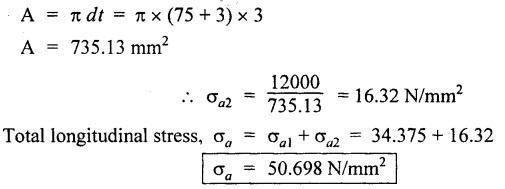


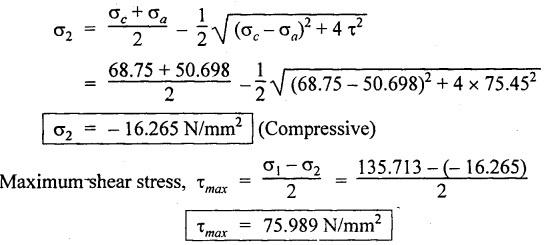




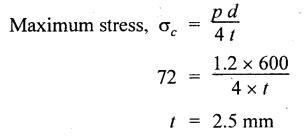

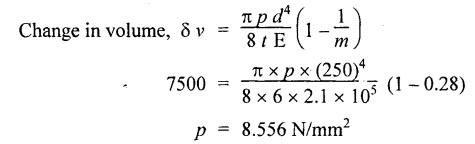




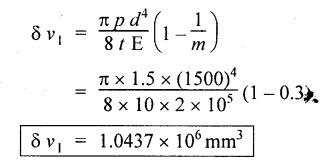
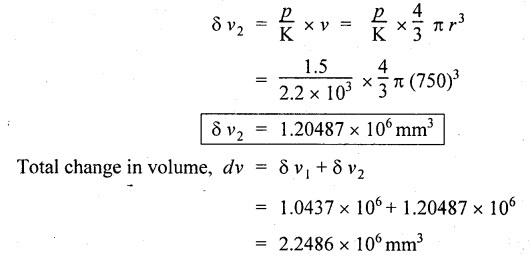













Strength of Materials: Unit V: Thin Cylinders, Spheres and Thick Cylinders : Tag: : Thin Cylinders, Spheres and Thick Cylinders - Strength of Materials - solved problems on thin cylinders and shells
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
