Engineering Physics: Unit II: Electromagnetic Waves
Solved Problems of Electromagnetic Waves
SOLVED PROBLEMS: Engineering Physics: Electromagnetic Waves
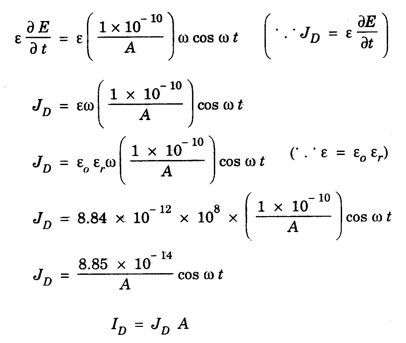
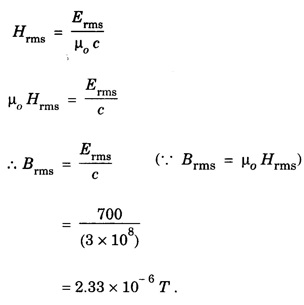
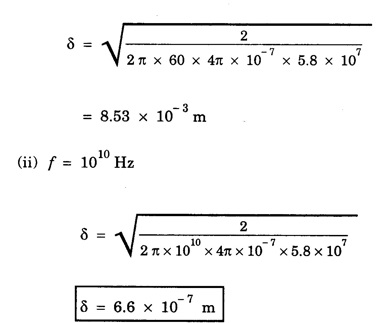
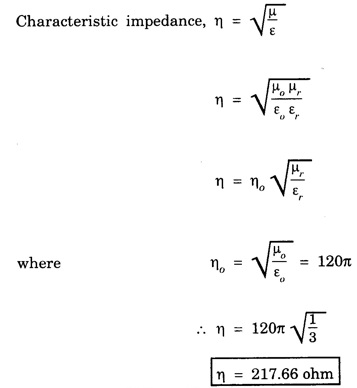
ANNA UNIVERSITY SOLVED PROBLEMS Problem 2.1: A circular cross section conductor of radius 2 mm carries a current Ic = 2.5 sin (5 × 108t) μ A. What is the amplitude of the displacement current density if σ = 35 M Ω-1'm-1 and εr = 1. Given data Ic = 2.5 sin (5 × 108t) μ A = 2.5 sin (5 × 108t) × 10-6A σ = 35 MS m-1= 3.5 × 106 S m-1 εr = 1 ε0 = 8.85 ×10-12 Fm-1 ω = 5 × 108 rads-1 radius a = 2 mm = 2 × 10-3 m Solution We know that JC = σE Taking only the amplitude IC Problem 2.2: The conduction current flowing through a wire with conductivity σ = 3 × 107 S/m and relative permittivity εr = 1 is given by Ic = 3 sin ωt (mA). If ω = 108 rad/sec. Find the displacement current. Given data Conductivity σ = 3 × 107Sm-1 Conducting current Ic = 3 sin ωt mA = 3 × 10-3 sin ωt A Angular frequency ω = 108 rad s-1 Solution: Displacement current density Since Ic is given, E is found from conduction current density as Jc = σE Multiplying both sides by ε substituting for JD Problem 2.3: A poor conductor is characterised by a conductivity σ = 100 (S/m) and permittivity ε = 4 ε0. At what angular frequency ω is the amplitude of the conduction current density Jc equal to the amplitude of the displacement current density JD? Given data Conductivity of the conductor σ = 100 Sm-1 Permittivity of the conductor ε = 4 ε0 Solution: Jc = σ E Equating conduction current density and displacement current density, we have σ E = ε ωe σ = ω ε 100 = ω x 4 ε 0 Problem 2.4: In a material for which σ = 5 S/m and εr = 1 the electric field intensity is E = 250 sin 1010t V/m. Find the conduction and displacement current densities and the frequency at which they have equal magnitudes. Given data Conductivity of medium σ = 5 Sm-1 Relative permittivity of medium εr = 1 Solution Conduction current density Jc = σ E Jc = 5 × 250 sin 1010t = 1250 sin 1010t Am-2 Displacement current density Problem 2.5: Find the conduction and displacement current densities in a material having conductivity of 10-3S/m and εr = 2.5 if the electric field in the material is E = 5.0 × 10-6 sin 9.0 × 109t + V/m. Given data Conductivity of the medium σ = 10-3 Sm-1 Relative permittivity εr = 2.5 Solution Conduction current density Jc = σE = 10-3 × 5 × 10-6 sin 9 × 109t Am-2 = 5 ×10-9 sin 9.0 × 109t Displacement current density Problem 2.6 : A light bulb of 20 W radiates energy isotropically, mostly in infrared region. Assuming it to be a point source find the irradiance (average energy per unit area per unit time or intensity) at a distance 1 m away. Calculate the strength of Given data: Power radiated by bulb P = 20 W Distance r = 1 m Solution: Irradiance is average energy per unit area per unit time at a distance 'r’ Intensity at a point is nothing but poynting vector at that point. ie., I = Savg substituting the given values, we have = 24.5 Vm-1 Problem 2.7 : The intensity of sunlight reaching the earth's surface is about 1300 W m-2 . Calculate the strength of electric and magnetic fields of the incoming sunlight. Solution: The time average Poynting's vector is But in electromagnetic wave from above relation Problem 2.8 : (i) Show that for a good conductor skin depth δ = λc/2 π, where λc, is the wavelength of electromagnetic waves in the conductor. (ii) Show that for an electromagnetic wave incident on a good conductor the electric vector reduces to about 1% at a depth of 0.73 % λc (iii) Find the wavelength and the propagation speed in copper for radio waves at 1 MHz. For copper assume μ = μ0, ε = ε0 and conductivity σ = 5.8 × 107Ω - m-1 Solution: (i) Suppose the wave is incident normally on the surface of the conductor along z-axis, then the electric field inside the conductor is given by k - wave vector For a good conductor and skin depth The wavelength of the wave in the conductor is (ii) Let us write taking in on both sides (iii) The required wavelength at 1 MHz = 1 × 106 Hz and the propagation speed Problem 2.9 : Find the depth of penetration of a plane wave in copper at a power frequency of 60 Hz and at microwave frequency 1010 Hz. Given σ = 5.8 × 107 mho m-1 Given data σ = 5.8 x 107 mho m-1 Depth of penetration (i) f = 60 Hz, σ = 5.8 × 107 mho m-1, μr = 1 μ0 = 4π × 10-7Hm-1 ω = 2πf Problem 2.10: A sinusoidal plane wave is transmitted through a medium whose electric field is 10 kV/m and relative permittivity of the medium is 4. Determine the mean rms power flow/unit area. Solution: E = 10 KVm-1 = 10 × 103 V m-1 εr = 4, μr = 1 Power flow/unit area is poynting vector Problem 2.11: Find the conducting behaviour of ground at 1 KHz, 10 MHz and 10 GHz. Given εr = 10 and σ = 5 × 10-3 mho/m. Solution: The ratio of conduction current to displacement current is σ/ωε which determines conducting behaviour For f = 1 kHz = 1 × 103 Hz ω = 2 πf σ = 5 × 10-3 mho m-1 εr = 10 For f = 1 MHz = 1 ×106 Hz For f = 10 GHz = 10 × 109 Hz = 9 × 10-4 At 1 KHz the ground acts like a good conductor and at 10 GHz it acts like an insulator. For 10 MHz ground acts like a quasi-conductor. Problem 2.12 : Find the skin depth 8 at a frequency of 1 MHz for copper where σ = 5.8 × 107S/m and μ = μ0. Also find the value of skin depth at 50 Hz. Given data Conductivity of the medium σ =5.8 × 107 Sm-1 Frequency f = 1 MHz = 1 × 106 Hz Solution: μ = μ0 μr and f = 1 MHz Substituting the given values, we have = 0.0661 × 10-3 m = 6.61 × 10-5m Also at f = 50 Hz, = 9.348 × 10-3 m Problem 2.13: Find the velocity of a plane wave in a lossless medium having a relative permittivity of 4 and a relative permeability of 1.2. Given data εr = 4; μr = 1.2 Solution: Velocity of EM wave in a medium is, Problem 2.14: Find the characteristic impedance of the medium whose relative permittivity is 3 and relative permeability is 1. Given data εr = 3; μr = 1 Solution: Problem 2.15: Find the velocity of a plane wave in a lossless medium having a relative permittivity of 5 and relative permeability of unity. Given data εr = 5, μr = 1 Solution: Velocity of propagation in the medium
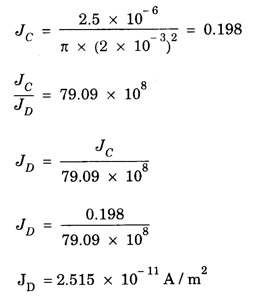
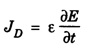

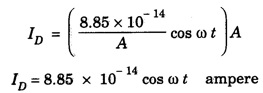
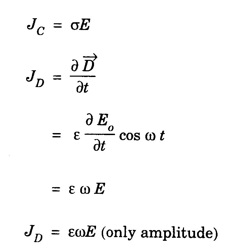
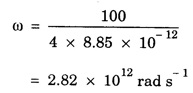
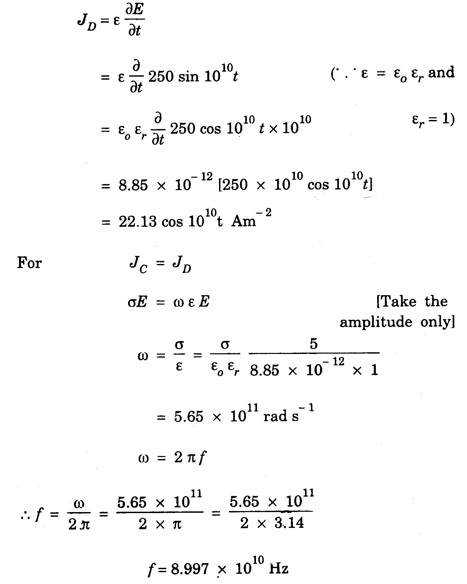
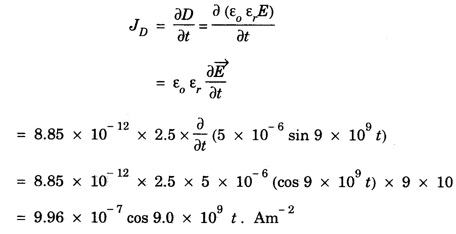
![]() -field associated with the radiation at this distance.
-field associated with the radiation at this distance.
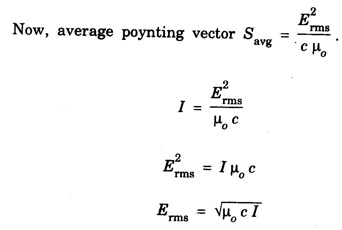
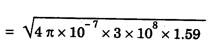
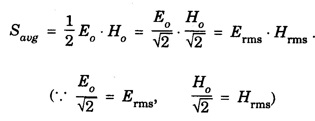

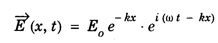


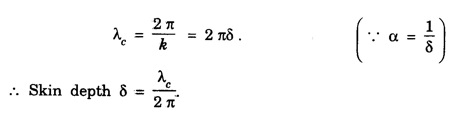
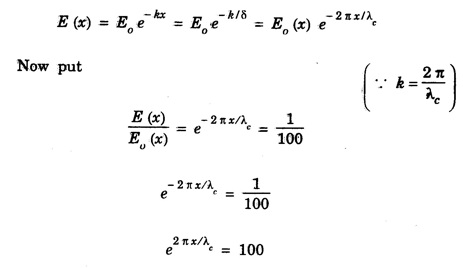
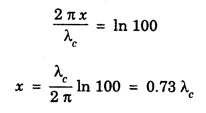

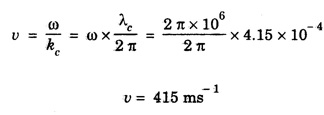
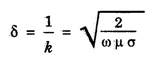

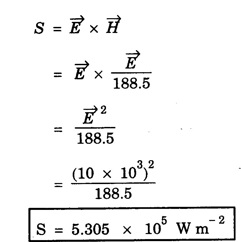
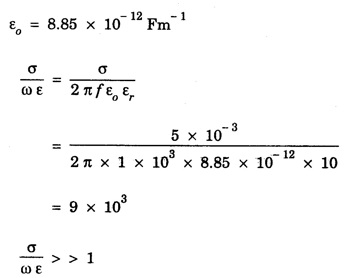
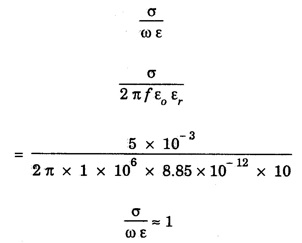
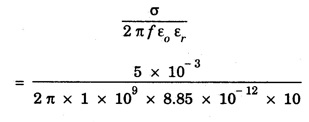
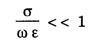
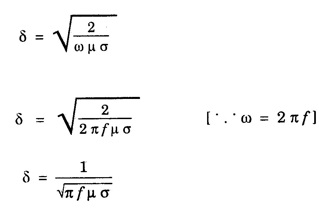
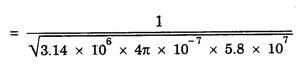

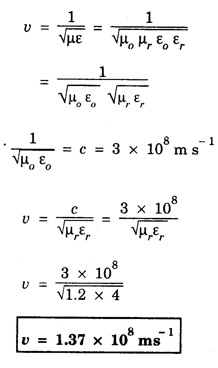

Engineering Physics: Unit II: Electromagnetic Waves : Tag: : - Solved Problems of Electromagnetic Waves
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
