Fluid Mechanics and Machinery: Unit 4: Turbines
Solved Examples based on pelton wheel (Turbine)
Solved Examples based on pelton wheel: Turbines - Fluid Mechanics and Machinery
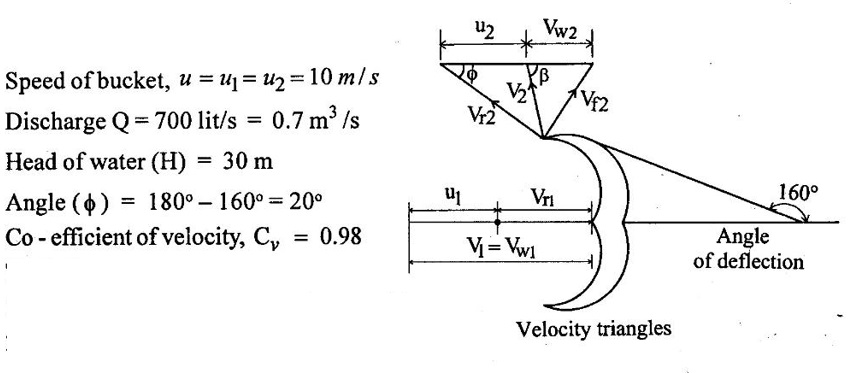
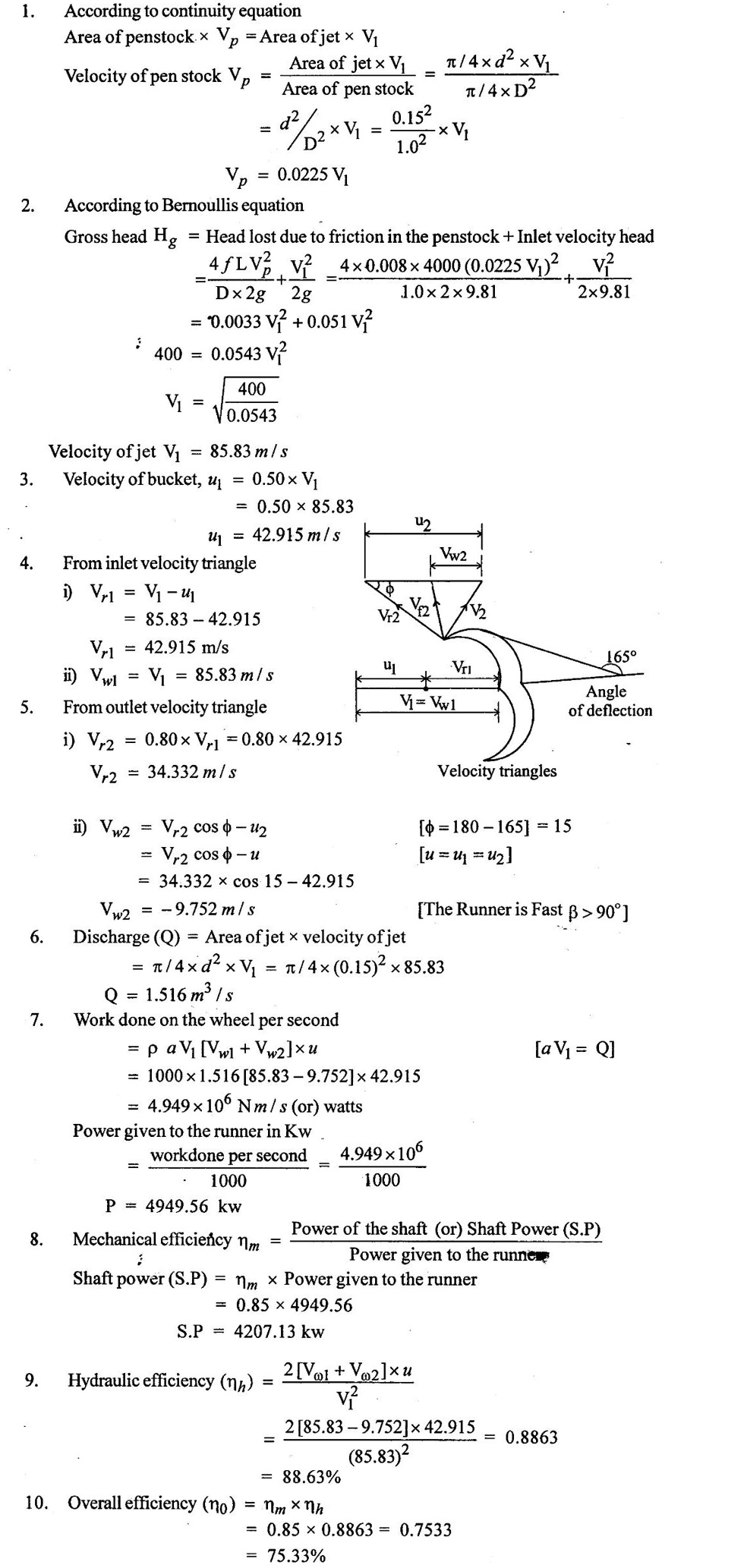
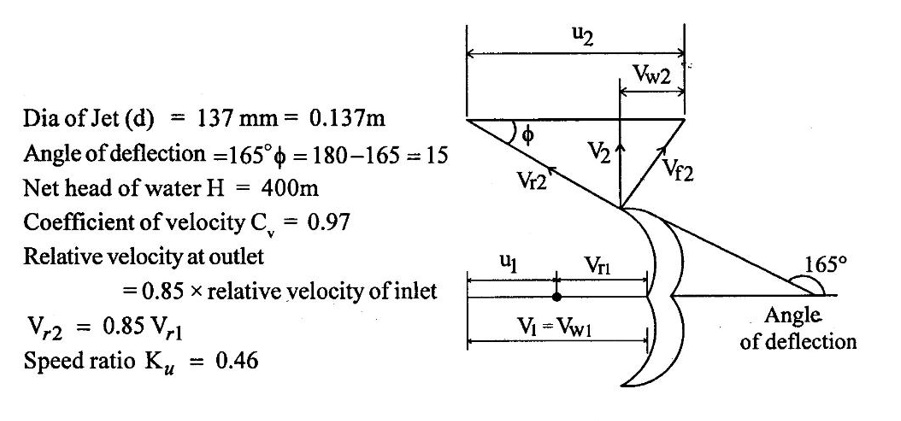
SOLVED EXAMPLES BASED ON PELTON WHEEL Example - 1 A pelton wheel is receiving water from a penstock with a grosshead of 510 m. One third of gross head is lost in friction in the penstock. The rate of flow through the nozzle fitted at the end of the penstock is 2.2 m3/s. The angle of deflection of the jet is 165o. Determine (i) The power given by water to the runner (ii) Hydraulic efficiency of the pelton wheel. Take co-efficient of velocity Cv = 1.0 and speed ratio = 0.45. Given data: To find: 1. Power given by water to the runner 2. Hydraulic efficiency of the turbine Solution: 5. Work done by the jet on the runner per second 6. Hydraulic efficiency (ηh) Result: 1. Power given by water to the runner (P) = 7139.8 kw 2. Hydraulic efficiency (ηh) = 97.3% Example - 2 A pelton wheel has a mean bucket speed of 10 meters per second with a jet of water flowing at the rate of 700 litres/sec under a head of 30 meters. The buckets deflect the jet through an angle of 160°. The calculate the power given by water to the runner and the hydraulic efficiency of the turbine assume co- efficiency of velocity as 0.98. Given data: To find: 1. Power given by water to the runner (p) 2. Hydraulic efficiency (ηh) Solution: Result: 1. Power given by water to runner (P) = 186.97 Kw 2. Hydraulic efficiency (ηh) = 90.75% Example - 3 A pelton wheel is having a mean bucket diameter of 1m and is running at 1000 rpm. The net head on the pelton wheel is 700m. If the side clearance angle is 15o and discharge through nozzle is 0.1 m3/s. Find i) Power available at the nozzle and ii) Hydraulic efficiency of the turbine. Given data: Diameter of wheel, D = 1.0 m Net head, H = 700 m Discharge Q = 0.1 m3/s Speed of wheel, N = 1000 rpm Side clearence angle ϕ = 15° To find: 1. Power available at the nozzle Solution: 2. Hydraulic efficiency of the turbine Solution: Result: 1. Power available at the nozzle (W.P) = 686.7 Kω 2. Hydraulic efficiency (ηh) = 97.18% Example - 4 A pelton wheel is working under a gross head of 400m. The water is supplied through penstock of diameter 1m and length 4 km from reservoir to the pelton wheel. The co-efficient of friction for the penstock is given as 0.008. The jet of water of diameter of 150mm strikes the buckets of the wheel and gets deflected through an angle of 165o. The relative velocity of water at outlet is reduced by 20% due to friction between inside surface of the bucket and water. If the velocity of the bucket is 0.50 times the jet velocity at inlet and mechanical efficiency is 85%. Determine i) power given to the runner ii) Shaft power iii) Hydraulic efficiency and overall efficiency. Given data: Gross head, Hg = 400 m Length of penstock, L = 4 km = 4000 m Diameter of jet (d) = 150 mm = 0.15 m Relative velocity at outlet, Vr2 = 0.80 Vr1 Diameter of penstock, D = 1.0 m Co-efficiency of friction, f = 0.008 Angle of deflection = 165° Mechanical efficiency (ηm) = 85% = 0.85 Velocity of bucket, u = 0.50 × Jet velocity at inlet (V1) To find: 1. Power given to the runner 2. Shaft power 3. Hydraulic efficiency 4. Overall efficiency Solution: Result: 1. Power given to runner = 4949.56 Kw 2. Shaft power (S.P) = 4207.13 kw 3. Hydraulic efficiency (ηm) = 88.83% 4. Overall efficiency (η0) = 75.33% Example - 5 A pelton wheel is to the designed for the following specifications: Shaft power = 11, 772 kw, Head 380 m, Speed, N = 750 rpm, Overall efficiency = 86%. Jet diameter is not to exceed one seventh of the wheel diameter. Determine (i) The wheel diameter (ii) The number of jets required, and (iii) Diameter of the jet Take, Kvl = 0.985 & Kul = 0.45 Given data: Shaft power S.P = 11,772 Kw = 11772 × 103w Head, H = 380 m Speed, N 750 rpm Overall efficiency η0 = 86% = 0.86 Ratio of jet diameter to wheel diameter = d/D 1/7 Coefficient of velocity Kv1 = Cv = 0.985 Speed ratio, Kul = 0.45 To find: (1) Wheel diameter (D) Solution: (2) No jets (q) (3) Diameter of Jet (d) Solution: Result: 1. Diameter of wheel (D) = 0.989 m 2. Diameter of jei (d) = 0.1412m 3. Number of jet required = 3 Example - 6 A 137 mm diameter jet of water issuing from a nozzle impinges on the buckets of a pelton wheel and jet is deflected through on angle of 165o by the buckets. The head available of the nozzle is 400m. Assuming coefficient of velocity as 0.97 speed ratio as 0.46 and reduction in relative velocities while passing through buckets as 15% find i) The Force exerted by the jet on buckets in tangential direction. ii) The power developed. Given data: (i) The force exerted by the Jet on buckets in tangentral direction (ii) Power developed Solution: Result: 1. Force exerted by Jet on backets in tangentral direction Fx = 104213.94 N 2. Power (P) = 4246.71 kw Example - 7 The following data is related to a pelton wheel: Head at the base of nozzle = 80 m, Discharge of the nozzle = 0.30 m3/s, Diameter of the jet = 100 mm Power of the shaft = 206 kw Power absorbed in mechanical resistance = 4.5 kw Determine (i) Power lost in nozzle and (ii) Power lost due to hydraulic resistance in the runner. Given data: Head at the base of the nozzle (H) = 80m Diameter of the Jet (d) = 100 mm = 0.1m Discharge (Q) 0.30 m3/s Power lost due to mechanical resistance = 4.5 kw Power of the shaft = 206 kw To find: i) Power lost in nozzle ii) Power lost due to hydraulic resistance in the runner Solution: 4. Power at base of nozzle = power of jet + power lost in nozzle 235.44 = 218.85 + power lost in nozzle Power lost in nozzle = 235.44 - 218.85 = 16.59 kw 5. Also power of the base of nozzle = Power at shaft+power lost in nozzle + power lost in runner + power lost due to mechanical resistance 235.44 = 206 + 16.59 + power lost runner + 4.5 Power lost in runner = 235.44 − (206 + 16.59 +4.5) = 8.35 kw Result: 1. Power lost in nozzle = 1659 kw 2. Power lost due to hydraulic resistance in runner = 8.35 kw Example - 8 A pelton wheel is to be designed for a head of 70 m when running at 200 rpm. The pelton wheel develops 94 kw shaft power. The velocity of buckets = 0.4 times the velocity of the jet. Overall efficiency = 0.85 and coeffienct of velocity is equal to 0.97. Given data: Head H = 70m Speed (N) = 200 rpm Overall efficiency η0 = 0.85 Shaft power (p) = 94 kw = 94 × 103 w Velocity of bucket u = 0.40 × velocity by of jet (V1) Coefficient of velocity Cv = 0.97 To find: Design a pelton wheel turbine Solution: 1. Velocity of jet = 35.947 m/s 2. Bucket velocity (a) u = 0.40 × V1 [for given] = 0.40 × 35.947 u = 14.378 m/s Result 1. Diameter of wheel (D) = 1.373 m 2. Diameter of Jet (d) = 0.0755 m 3. Width of buckets (B) = 0.302 m 4. Depth of buckets (T) = 0.0906 m 5. No of buckets (z) = 24 Example - 9 A pelton turbine is required to work under a head of 50m to develop 150 kw at 250 rpm. Assuming velocity coefficient for nozzle = 0.96 speed ratro = 0.46, overall efficiency = 96% Clearence angle of bucket = 15o, bucket friction factor = 0.84. Find no of Jets, diameter of Jets, diameter of runner, no of buckets if the jet ratio is not to be less than 10. Given data: Head (H) = 50 m Speed (N) = 250 rpm Speed ratio (Ku) = 0.46 Clearce angle of bucket ϕ = 15° Power (P) = 150 kw = 150 × 103 w Coefficient of velocity Cv = 0.96 Mechanical efficency (ηm) = 96% = 0.96 Bucket friction factor (K) = 0.84 Jet ratio = D/d should to greater than 10 To find: 1. No of jets 2. Diameter of jets 3. Diameter of runner 4. No of buckets Solution: Solution: Result 1. Diameter of runner (D) = 1.056 m 2. Diameter ofjet (d) = 0.11m 3. No of jet required (n) = 2 4. No of bucket (z) = 20 Example - 10 Design a pelton wheel which rotating under a head of 70 m at 350 rpm. It produces a power of 120 kw with an overall efficience is 88%. The speed ratio for the turbine is 0.45 and the coefficient of velocity of nozzle is 0.98. Given data: Head (d) = 70m Speed (N) = 350 rpm Power (p) = 120 kw = 120 × 103 w Speed ratio Ku = 0.45 Overall efficiency η0 = 88% = 0.88 Co-efficient of velocity Cv = 0.98 To find : Design a pelton wheel Solution: 7. Width of bucket B = 4d = 4 × 0.0834 = 0.3336 m 8. Depth of bucket T = 1.2 × d = 1.2 × 0.0834 = 0.100m 9. Length of buckets (L) = 2.5 × d = 2.5 × 0.0834 = 0.2085m 10. Notch width = 1.15 d = 1.15 × 0.0834 = 0.095 m Result: 1. Runner diameter (D) = 0.892m 2. Diameter of Jet (d) = 0.0834m 3. No of buckets (z) = 21 4. Width of buckets (B) = 0.3336 m 5. Depth of buckets (T) = 0.100m 6. Length of buckets (L) = 0.2085 m 7. Notch width = 0.095 m Example - 11 A pelton turbine delivery a max power of 15000 kw when working under a head of 500m and running at 800 rpm. Find diameter of orifice at nozzle tip, least diameter of jet and mean diameter of wheel specify no of bucket for wheel. Take η0 = 0.9 η0 = 0.8 Cv = 0.98 Kv = 0.45 Is Jet ratio with in limit? Given data: Power (p) = 15000 kw = 15 × 106 w Speed (N) = 800 rpm Hydraulic efficiency (ηh) = 0.8 Speed ratio (Ku) = 0.45 Head (H) = 500m Overall efficiency (η0) = 0.9 Co-efficient of velpcity (Cv) = 0.98 To find: 1. Diameter of orifice of nozzle tip (d) 2. Least diameter of Jet (d) 3. Whirl velocity at outlet (Vω2) 4. Mean diameter of wheel (D) 5. No of bucket (z) 6. Check Jet ratio limit Solution: 5. Discharge (Q) = Area of Jet Velocity of Jet = π/4× = π/ 4 × d2 × V1 d2 = 0.04456 Diameter of jet (d) = 0.211 m Limit of Jet ratio 12 hence this ratio not adequate. So take value min Jet ratio 12 Result 1. Orifice diameter (d) = 0.211 m 2. Least diameter of jet (d) = 0.0886 m 3. Diameter of runner (D) = 1.064 m 4. Whirl velocity at outlet (Vw2) = − 12.52 m/s 5. No of bucket (z) = 18 Example - 12 At a hydroelectric plant, the difference in water levels in the intake and tail race is 180m. When the flow is 3.25 cumec friction loss in penstock is 18 m and head utilized by turbine 140m. The mechanical friction in turbine 80 kw and leakage loss is 90 LPS find (a) Hydraulic, volumetric, mechanical and overall efficiency (b) Power delivered to shaft (c) Power delivered to runner Given data: Total head (Hg) = 180m Discharge (Q) = 3.25 cumec or 3.25 m3/s Friction loss in per stock stock (hf) = 18m Head on the turbine (H) = 140m Friction loss due to mechanical aspect = 75 kw = 75 × 103w leakage loss 90 LPS = 90 × 10-3 m3/s To find: 1. Hydraulic efficiency 2. Volumetric efficiency 3. Mechanical efficiency 4. Overall efficiency 5. Power deliver to shaft 6. Power delivered to runner Solution: 1. Runner power = WQH (H utilized by turbine) = 9810 × 3.25 × 140 = 4.463 × 106 watts 2. Water power (supplied to turbine) = WQH net = WQ (Hg − hƒ) = 9810 × 3.25 × (180 – 18) = 5.165 × 106 w 6. Overall efficiency (η0) = ηm × ηh × ηv = 0.9831 × 0.8640 × 0.9723 = 0.8258 = 82.58 % 7. Power delivered to shaft = Shaft power = 4.388×106 w 8. Power delivered to runner = Runner Power = 4.463×106 w Result: 1. Hydraulic efficiency (ηh) = 86.40% 2. Volumetric efficiency (ηv) = 97.23% 3. Mechanical efficiency (ηm) = 98.31% 4. Overall efficiency (η0) = 84.93% 5. Shaft power (SP) = 4.388 × 106 w 6. Runner power (RP) = 4.463 × 106w Example - 13 A pipe line 1400 m long supplies at 700 LPS to a pelton wheel head above nozzle is 400m. CV = 0.96 friction Factor 0.03, η0 = 85%, N = 660 rpm hƒ = 13m find 1. Power developed (HP) 2. Nozzle diameter 3. Pipe diameter Given data: Cross head (Hg) = 400m Length of pipe (L) = 1400 m Co effient of velocity (cv) = 0.96 Friction factor (f) = 0.03 Loss of head due to friction (hf) = 13m Overall efficiency (η0) = 85% = 0.85 Speed (N) = 660 rpm Discharge (Q) = 700 LPS = 700 × 10-3 m3/s To find: 1. Power developed (HP) 2. Nozzle diameter (or) Jet diameter 3. Pipe diameter (D) Solution: 1. Net head (H) = Hg − hƒ = 400 - 13 = 387 m 4. Discharge (Q) = Area of the Jet - Velocity of jet Diameter of Jet (d) = 0.1032m Result: 1. Power developed in (HP) = 3072.10 HP 2. Diameter of Jet (d) = 0.1032 m 3. Pipe diameter (D) = 0.666 m Example - 14 A double Jet pelton wheel is required to generate 7500 kw under a head of 400m. The jet is deflected through 165o and relative velocity of Jet is reduced by 15% in passing over the buckets find 1. Dia of each Jet 2. Totall flow rate 3. Force exerted by Jet on bucket in tangentral direction 4. Hydraulic efficiency if K = 0.9 Assume η0 = 80%, generator efficiency = 95% Cv = 0.97 and Ku = 0.46 Given data: 1. Dia of each jet 2. Total flow rate 3. Force exerted by jet on tengentral direction 4. Hydraulic efficiency Solution: 3. Total mess flow rate m = ρ × Q = 1000 × 2.51 = 2510 kg/s 6. From inlet velocity triangles 7. From outlet velocity triangle 8. Force exerted by each Jet on bucket 9. Discharge Q = a × V1 Area of jet (a) = Q/V1 Result: 1. Dia of each jet (d) = 0.136 m 2. Total flow rate (Q) = 2510 kg/s 3. Force exerted by jet (F) = 206.51 × 103 N 4. Hydraulic efficiency (ηh) = 93.21% Example - 15 A twin jet pelton wheel runs at 330 rpm under a head of 550m. The jet diameter is 10 cm and gets deflected through 165°. If Vr2 = 0.85 Vr1, Cv = 0.98 kv = 0.46 calculate i) wheel diameter 2. Power developed 3. η0 4. ηh 5. ηm Given data: Speed (N) = 330 rpm Jet diameter (d) = 10 cm = 0.1 m head (H) = 550m Angle of Deflection (θ) = 165° Cv = 0.98 kv = 0.46 To find: 1. Wheel diameter (D) 2. Power developed (P) 3. η0 4. ηh 5. ηm Solution: Result: 1. Wheel diameter (D) = 2.76 m 2. Power developed (p) = 7462.65 kw 3. Overall efficiency (η0) = 87.09% 5. Mechanical efficiency (ηw) = 96.03% 4. Hydraulic efficiency (ηh) = 90.69% Example - 16 A pelton wheel having semicircular bucket function under a head of 150m and consumer 50 lit/sec of water. If 60 cm diameter wheel makes 600 rotations per minute. Calculate net power available at the nozzle and hydraulic efficiency of wheel Assume Cv = 1 and bucket if smooth. Given data: Head (H) = 150 m Speed (N) = 600 rpm Discharge (Q) = 50 lit/sec = 50×10−3 m3 / s Diameter of wheel D = 60 cm = 0.60m Cv = 1 To find: 1. Power available at nozzle or water power 2. Hydraulic efficiency (ηh) Solution: Result: 1. Hydraulic efficiency (ηh) = 90.67% 2. Water power (W.P) = 73.57 kw Example - 17 A pelton wheel develops 8 MW the working under a head of 400m. It rotates at 400 rpm. Determine i) the diameter of wheel ii) Quantity of water required iii) no of jets take jet ratio = 12, η0 = 85% Cv = 0.96 and ku = 0.45. Given data: Power (P) = 8 Mw, Speed (N) = 400 rpm, ku = 0.45. Head (H) = 400m η0 = 85%, Cv = 0.96 Jet ratio = 12. To find: 1. Quantity of water required (Q) 2. No of Jets 3. Diameter of wheel (D) Solution: Result: 1. Diameter of wheel (D) = 1.903m 2. Quantity of water required (Q) = 2.348 m3 / s 3. No of Jet (n) = 2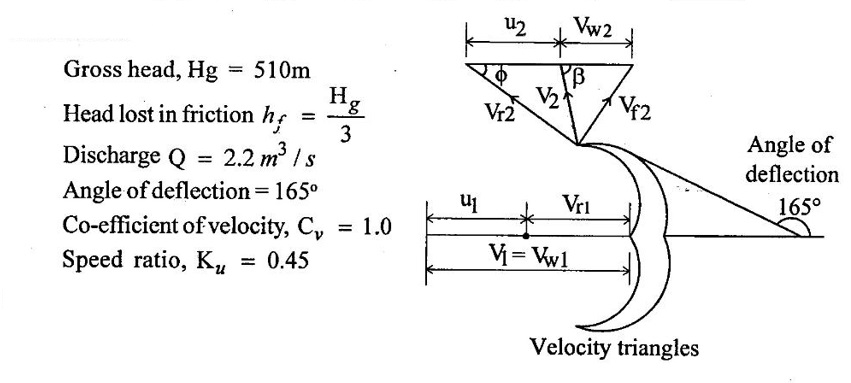


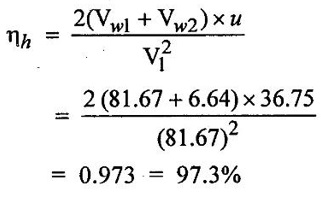



 To find:
To find:

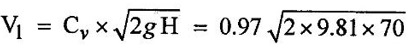




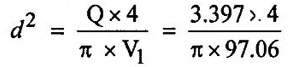




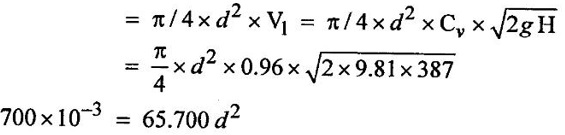
 To find:
To find:
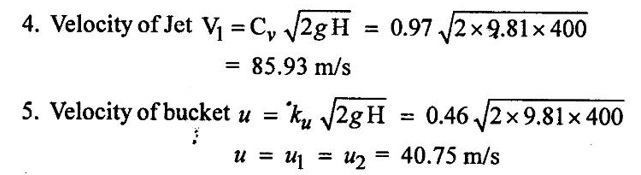
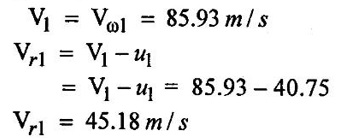
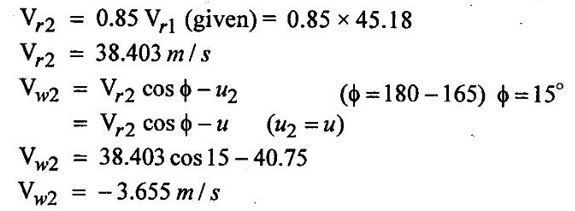
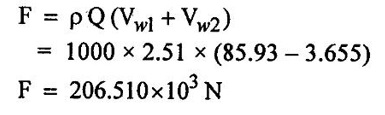




Fluid Mechanics and Machinery: Unit 4: Turbines : Tag: : - Solved Examples based on pelton wheel (Turbine)
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
