Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics
Solved Examples Based on Momentum Equation
Fluid Mechanics
Solved Examples Based on Momentum Equation: Fluid Properties and Flow Characteristics - Fluid Mechanics and Machinery
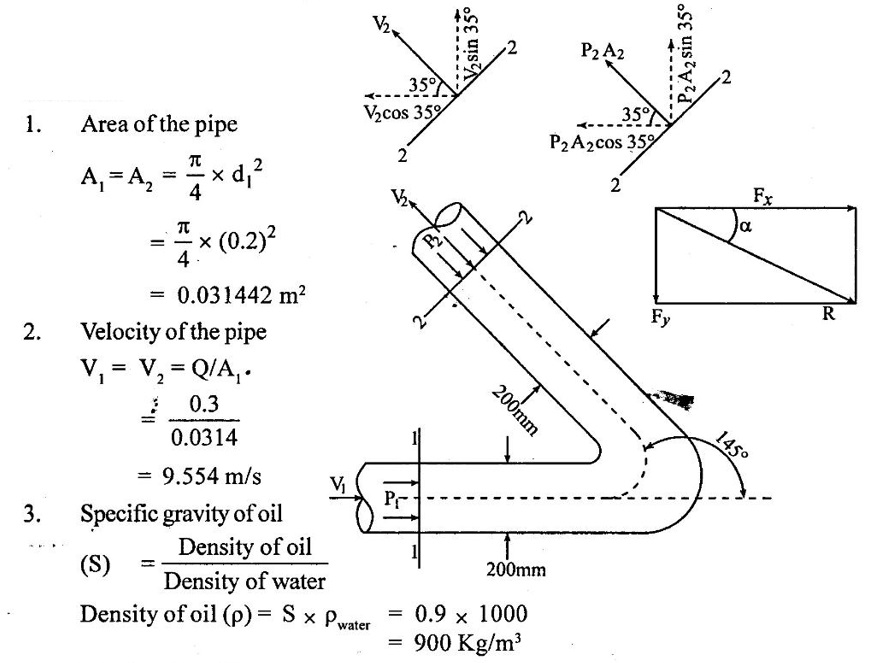
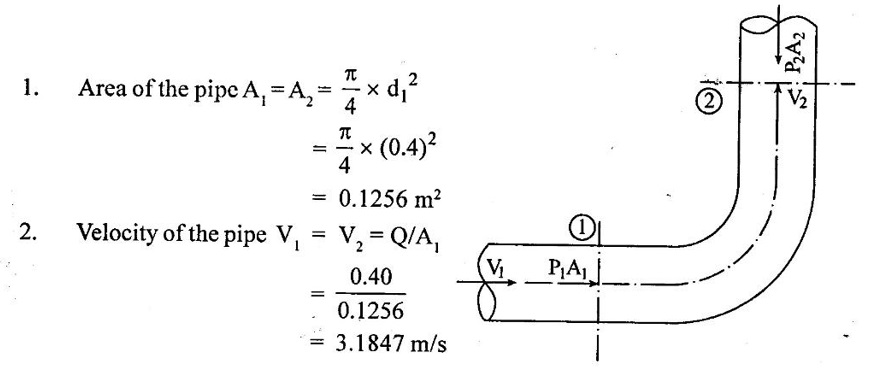
SOLVED EXAMPLES BASED ON MOMENTUM EQUATION Example - 86 A 50° reducing bend is connected in a pipeline, the diameters at the inlet and outlet of the bend being 700mm and 350mm respectively. Find the force exerted by the water on the bend if the intensity of pressure at inlet to bend is 9.2N/cm2 and rate of flow of water is 500 lits/sec. Also find the angle made by the resultant force with horizontal direction. Given data: Angle of bend (θ) = 50° Inlet diameter (d1) = 700mm = 0.7m Outlet diameter (d2) = 350mm = 0.35m Intensity of pressure at inlet (P1) = 9.2N/cm2 = 9.2 × 104 N/m2 Rate of flow (Q) = 500 lits/sec = 0.5m3/sec To find: 1. Resultant force (FR) 2. Angle made by the resultant force with horizontal direction. Solution: 5. Net force acting in x-direction Fx = ρQ(V1 - V2 cosθ) + P1 × A1 - P2 × A2 cosθ Fx = 1000 × 0.5(1.299-5.197 cos 50) + 9.2 × 104 × 0.3848 - 7.93 × 104 × 0.0962 cos 50 Fx = 500 × (−2.04156) + 35.4016 × 103 – 4903.60 Fx = -1020.78 + 35.4016 × 103 - 4903.60 Fx = 29477.22 Fx = 29.477 kN 6. Net force acting in y-direction Fy = ρQ (-V2y sinθ) – P2yA2 sinθ Fy = 1000 × 0.5(-5.197 × sin 50) - 7.93 × 104 × 0.0962 sin 50 Fy = -1990.56 - 5843.89 Fy = -7834.45N 7. Resultant force (FR) FR = 30500.57Ņ 8. Angle made by Resultant force Result : (i) Resultant force (FR) = 30500.57 N (ii) Angle made by Resultant force (θ) = 14°53' Example - 87 300 lit/sec of oil flowing through a pipe having a diameter of 200mm. If the pipe is bent by 145o (that is changed from initial to final direction is 145o), find the magnitude and direction of the resultant force on the bend. The pressure of oil flowing is 40N/cm2 and specific gravity of oil is 0.9. Given data: Diameter of pipe d1 = d2 = 200mm = 0.2m Rate of flow Q = 300 lits/sec = 0.3 m/sec Angle of bend θ = 180-145=35° Pressure of the pipe P1 = P2 = 40N/cm2 = 40 × 104N/m2 Specific gravity of oil (S) = 0.9 To find: Resultant force Solution: 4. Net force in x-direction Fx = ρQ(V1x - V2 cosθ) + P1xA1 + P2x A2 cosθ V2 Applied in opposite direction so -ve sign and P2 in same direction so + sign Fx = ρQ(V1x - (-V2 cosθ) + P1xA1 + P2x A2 cosθ Fx = ρQ(V1x + V2 cosθ) + P1xA1 + P2x A2 cosθ Fx = 900 × 0.3(9.549 + 9.549 cos 35) + 40 × 104 × 0.0314 + 40 × 104 × 0.0314 × cos35 = 270 × 17.3710 + 12560 + 10288.54 = 4690.17 +12560 + 10288.54 = 27538.71 N 5. Net force acting in y-direction Fy = ρQ(−V2y sinθ) – P2y A2 sinθ Fy = 900 × 0.3(−9.549 × sin 35) - 40 × 104 × 0.0314 × sin35 = 270 × (-5.477) - 7204.12 = - 8682.91 N 6. Resultant Force (FR) FR = 28,875.14N Result : Resultant Force (FR) = 28,875.14N Example - 88 A pipe of 400mm diameter conveying 0.4m3/s of water has a right angled bend in a horizontal plane. Find the resultant force exerted on the bend if the pressure at inlet and outlet of the bend are 25N/cm2 and 23N/cm2 Given data: Angle of bend (θ) = 90° Pipe diameter d1 = d2 = 400mm = 0.4m Discharge (Q) = 0.4m3/s Inlet pressure (P1) = 25N/cm2 = 25 × 104 N/m2 Outlet pressure (P2) = 23N/cm223 × 104N/m2 To find: Resultant force (FR) Solution: 3. Net force in x-direction Fx = ρQ(V1x - V2 cosθ) + P1x A1 + P2x A2 cosθ V2 Applied in same direction so + ve sign and P2 in opposite direction so-ve sign Fx = ρQ(V1x - V2 cosθ) + P1x A1 + P2x A2 cosθ Fx = 1000 × 0.40(3.2847-(+ 3.2847 cos 90) + 25 × 104 × 0.1256 -23 × 104 × 0.1256 × cos 90 Fx = 1000 × 0.40(3.2847-0) + 25 × 104 × 0.1256 - 0 = 1313.88 + 31400 Fx = 32713.88 N 4. Net force in y-direction Fy = ρQ(-V2y sinθ) - P2y A2 sinθ Fy = 1000 × 0.4 (-3.1847 × sin 90°) - 23 × 104 × 0.1256 × sin 90 = 400 × (-3.1847) - 28888 Fy = -30161.88N 5. Resultant Force (FR) FR = 44496.48 N Result : Resultant Force (FR) = 44496.48 N Example - 89 A nozzle of diameter 30mm is fitted to a pipe of diameter 50mm. Find the force exerted by the nozzle on the water which flowing through the pipe at the rate of 2.3m3/min. Given data: Pipe diameter d1 = 50mm = 0.05m Nozzle diameter d2 = 30mm = 0.03m Rate of flow (Q) = 2.3m3/min = 0.0383m3/s To find: Force exerted by nozzle Solution: = 0.0007068 m2 3. Discharge (Q) Q = A1V1 = A2V2 V1 = Q/A1 = 0.0383 / 0.001963 = 19.510 m/s V2 = Q/A2 = 0.0383/0.0007068 = 54.187 m/s P1 = 9810 × 130.254 P1 = 1277791.74 N/ m2 4. Force exerted by nozzle Net force in x-direction = Rate of change of momentum P1A1 - P2A2 + Fx = ρ Q (V2 − V1) Fx = ρQ (V2 - V1) − P1A1 − P2A2 = 1000 × 0.0383 (54.187 - 19.510) - 1277791.74 × 0.001963 – 0 × 0.0007068 = 1328.129 - 2508.305 Fx = -1180.18 N Result : Force exerted by nozzle Fx = -1180.18 N Example - 90 The diameter of a pipe gradually reduces from 1.5m to 0.9m and the pressure intensity is 8KN/m2 at inlet. The rate of flow of water through the pipe is 500lit/sec. Find the intensity of pressure at the outlet and also determines the force exerted by flowing water on the transition of the pipe. Given data: Diameter at inlet (d1) = 1.5m Diameter at inlet (d2) = 0.9m Intensity of pressure at inlet (P1) = 8KN/m2 = 8 × 103 N/m2 The rate of flow (Q) = 500lit/s = 0.5m3/s To find: 1. Intensity of pressure at the outlet (P2) 2. Force exerted by flowing water on the transition of the pipe (Fx) Solution: 1. Area of the pipe at inlet (A1) 2. Area of the pipe at outlet (A2) = 0.636 m2 3. Discharge (Q) Q = A1V1 = = A2V2 V1 = Q/A1 = 0.5/1.767 = 0.282m/s V2 = Q/A2 = 0.5/0.636 = 0.786 m/s 4. Force exerted by flowing water on the transition of the pipe (Fx) Net force in x- direction = Rate of change of momentum P1A1 – P2A2 + Fx = ρ Q (V2 − V1) Fx = ρ Q (V2 − V1) - P1A1 – P2A2 = 1000 × 0.5(0.786-0.282) - 8 × 103 × 1.767 + 7726.356 × 0.636 = 252 – 14136 + 4913.96 Fx = -8970.04 N Force exerted by flowing water on the transition of the pipe = - Fx = -(-8970.04) = 8970.04 N Result : Force exerted by flowing water on the transition of the pipe (Fx) = 8970.04 N
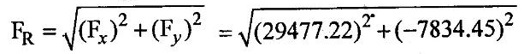
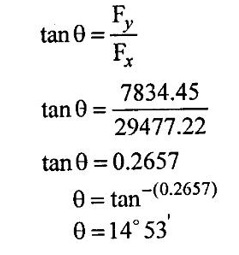
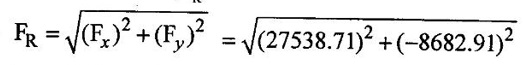
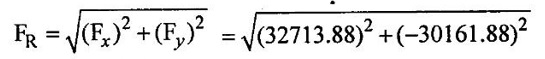
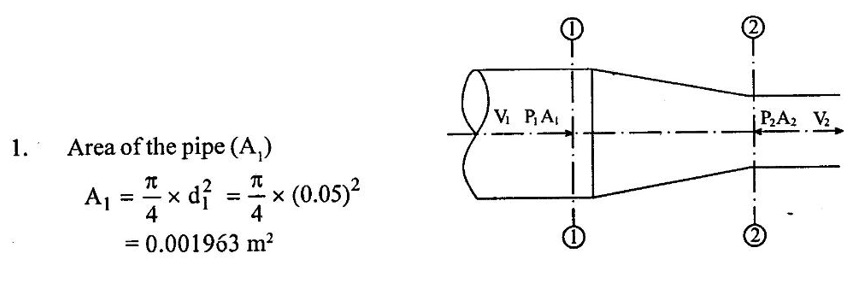 2. Area of the pipe at outlet (A2)
2. Area of the pipe at outlet (A2)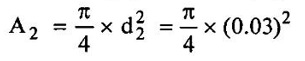

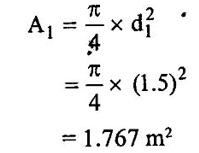
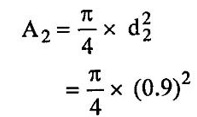
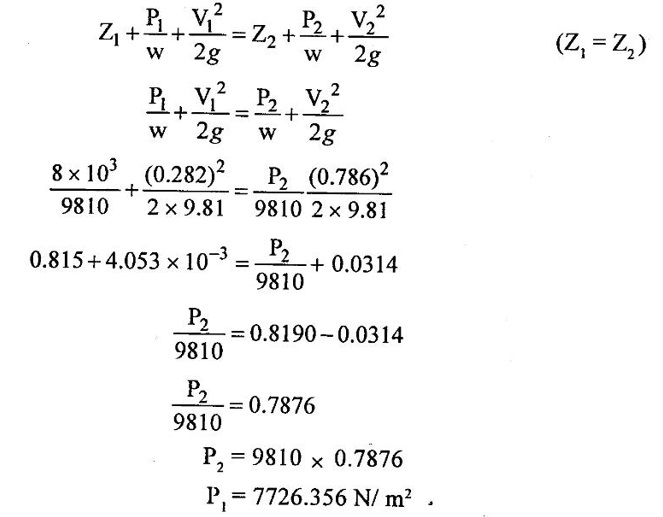
Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics : Tag: : Fluid Mechanics - Solved Examples Based on Momentum Equation
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
