Fluid Mechanics and Machinery: Unit 4: Turbines
Solved Examples based on inward flow reaction turbine
Solved Examples based on inward flow reaction turbine: Turbines - Fluid Mechanics and Machinery
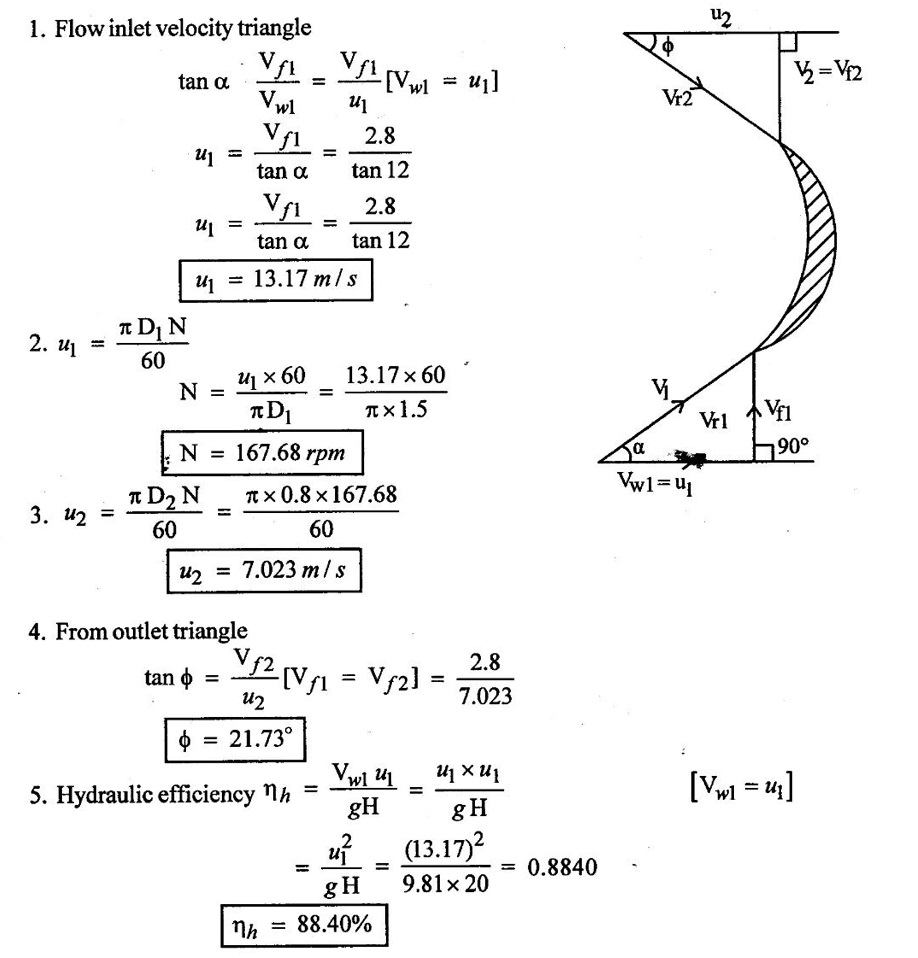
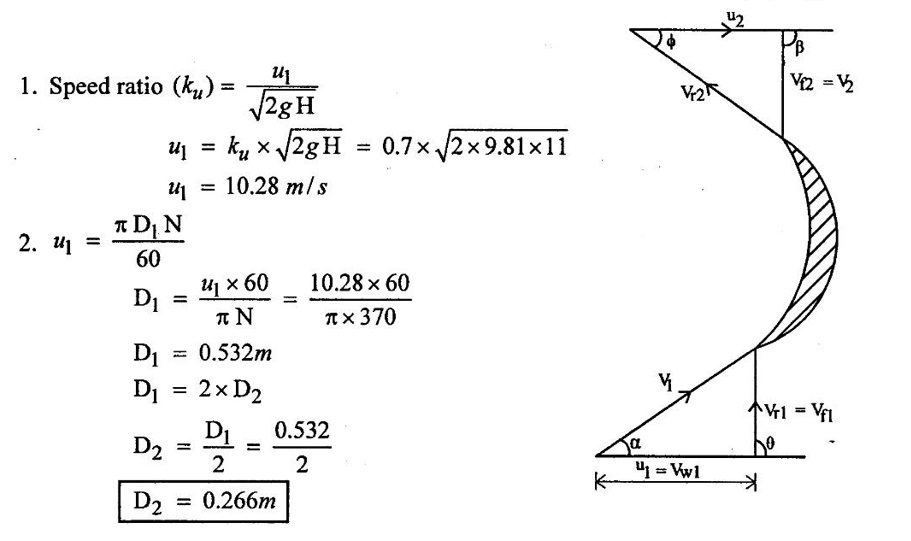
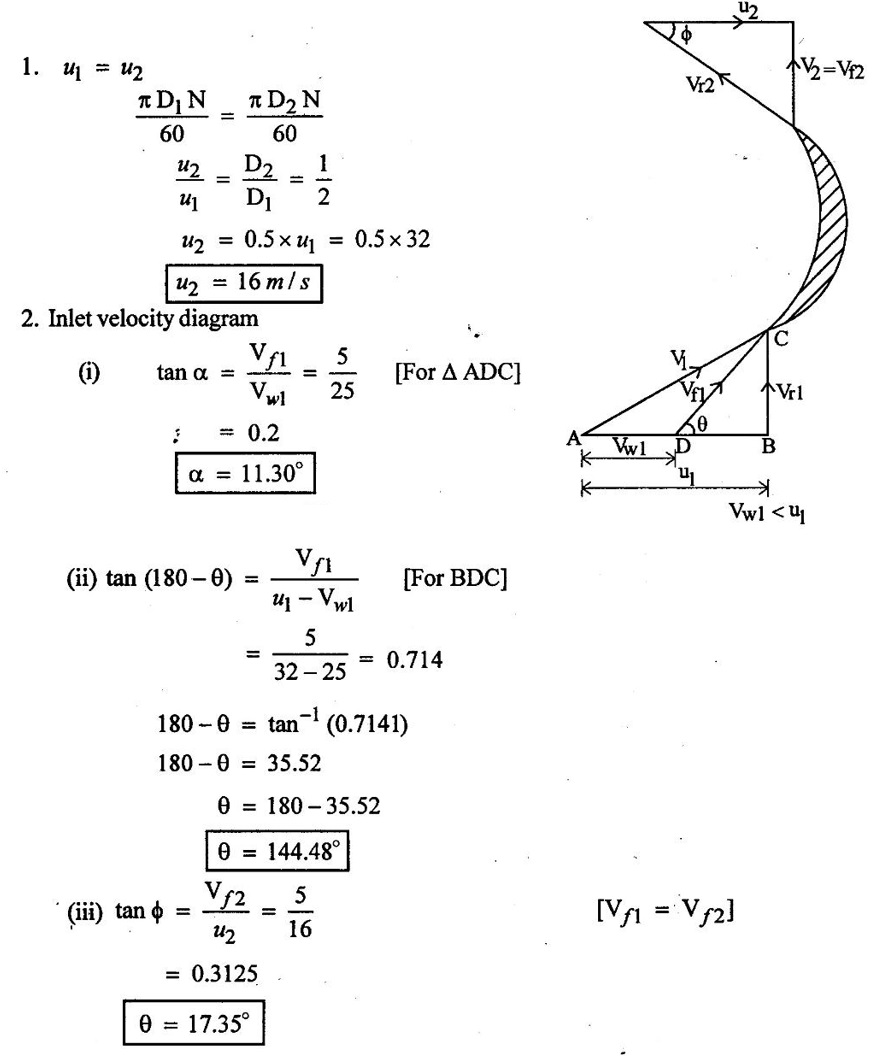
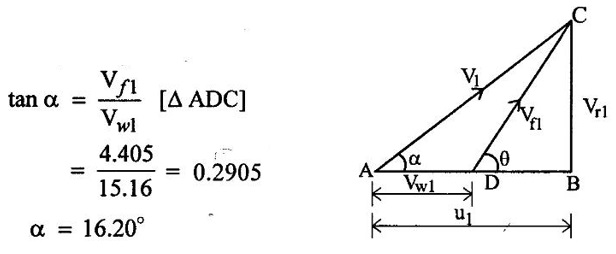
SOLVED EXAMPLES BASED ON INWARD FLOW REACTION TURBINE Example - 18 An inward flow reaction turbine has external diameter and internal diameters 1m and 0.5m respectively the turbine is running at 250 rpm and width of turbine at inlet in 190mm. The velocity of flow through the runner is constant and equal to 3.2 m/s. The guide blade move an angle of 10o of the tangent of the wheel and the discharge at the outlet of the turbine is radial determine. 1. The absolute velocity of water at inlet of runner. 2. The velocity of whirl at inlet 3. The relative velocity at inlet 4. The runner blade angle 5. Width of the runner at outlet 6. Mass of water flowing through the runner per sec. 7. Head at the inlet of the turbine 8. Power developed and hydraulic efficiency of the turbine. Given data: External diameter (D1) = 1m Width at inlet (B1) = 190mm = 0.19m Velocity of flow (Vƒ1) = Vƒ2 = 3.2 m/s Discharge at outlet = radial Internal diameter (D2) = 0.5m Speed (N) = 250 rpm Guide blade angle (α) = 10° Β = 90°, Vw2 = 0 To find: 1. Absolute velocity of water of inlet of the runner (V1) 2. Velocity at whirl at inlet (Vw1) 3. Relative velocity of inlet (Vr1) 4. The runner blade angles θ and ϕ 5. Width of the runner at outlet (B2) 6. Mass of water flowing through the runner per sec 7. Head at inlet of turbine (H) 8. Power developed (P) 9. Hydraulic efficiency (ηh) Solution: (iii) Relative velocity at inlet (iv) Runner blade angle (θ) 3. Flow outlet triangle 4. Width of runner at outlet (B2) Q1 = Q2 6. Mass of water flowing through the runner per sec m = ρ × Q = 1000 × 1.91 7. Head at inlet (H) Result: 1. Absolute velocity at water at inlet V1 = 18.43 m/s 2. Velocity of whirl at inlet (Vwl) = 18.15 m/s 3. Relative velocity at inlet (Vr1) = 5.99 m/s 4. Runner blade angles θ = 32.29°, ϕ = 26.05° 5. Width of the runner at outlet (B2) = 0.38m 6. Mass of water flowing per sec (m) = 1910 kg/s 7. Head at inlet (H) = 24.73m 8. Power developed (P) = 453.75 kw 9. Hydraulic efficiency (hh) = 97.92% Example - 19 An inward flow reaction turbine has external and internal diameter as 1m and 0.6m respectively. The hydraulic efficiency of the turbine is 90% when head on the turbine is 36 m. The velocity of flow at outlet 2.5 m/s and discharge at outlet is radial if the vane angle at outlet is 15o and width of the wheel is 100 mm at inlet and outlet. Determine the guide blade angle, speed of the turbine, vaňe angle of the runner at inlet, Volume flow rate of turbine, and power developed. Given data: External diameter D1 = 1.0m Hydraulic efficiency ηh = 90% = 0.9 Velocity of flow at outlet Vf2 = 2.5 m/s Width at wheel B1 = B2 = 100 mm = 0.1m Internal diameter D2 = 0.6m Head (H) = 36 m Discharge is radial Vw2 = 0 Vane angle at outlet ϕ = 15° To find: 1. Guide blade angle (a) 2. Speed of the turbine (N) 3. Vane angle of the runner at inlet (θ) 4. Volume flow rate of turbine (Q) 5. Power developed (P) Solution: 5. Volume of flow of water Q = π D2 Vƒ2 В2 = π × 0.6 × 2.5 × 0.1 Q = 0.4712 m3/s 6. Volume of flow water Q2 = Q1 = π D1 Vƒ1 B1 7. Guide blade angle (α) 8. Runner angle at inlet (θ) 9. Work done (or) power (P) = ρQ (Vwl u1) = 1000 × 0.4712 × 20.46 ×15.52 = 149.57 × 103 w Result: 1. Guide blade angle at inlet (α) = 4.192° 2. Vane angle at inlet (θ) = 16.97° 3. Speed of the turbine (N) = 298.6 rpm 4. Volume flow rate of turbine (Q) = 0.4712 m/s 5. Power developed (P) = 149.57 Kw Example - 20 An inward flow reaction turbine has an exit diameter of 1.25 m and its breath at inlet is 300 mm. If the velocity of flow at inlet is 3.0 m/s. Find the mass of water passing through the turbine per sec. Assume 9% of the of the flow is blocked by blade thickeness if the speed of the runner is 200 rpm and guide blade angle at inlet is 10° to the wheel tangent find. (i) The runner vane angle of inlet (ii) Velocity of wheel at inlet (iii) The absolute velocity of water leaving the guide vanes. (iv) The relative velocity of water entering the runner blade. Given data: External diameter (D1) = 1.25m Area blocked by vanes = 9% Speed (N) = 200 rpm Breath inlet (B1) = 300 mm = 0.3 m Velocity of flow at inlet Vƒ1 = 3.0 m/s Guide blade angle α = 10° To find: (i) Runner vane angle at inlet (Q) (ii) Velocity of wheel at inlet (u1) (iii) Absolute velocity of water leaving the guide vane (V1) (iv) The relative velocity of water enteriry the runner (Vr1) (v) Mass of water passing through the turbine sec (m) Solution: Result: 1. Mass of water passing through/sec m=3216 K/s 2. Runner vane angle at inlet θ = 66.41° 3. Absolute velocity of water at inlet = 17.27 m/s 4. Relative velocity of water inlet 3.273 m/s Example - 21 The external and internal diameter at an inward flow reaction turbine are 1.5 m and 0.8m respectively the head on the turbine is 20m and velocity of flow through the runner is constant and equal to 2.8 m/s the guide blade angle is given as 12o and the runner vanes are radial at inlet. If the discharge at outlet is radial determine. (i) Speed of the turbine (ii) The vane angle at outlet of runner (iii) Hydraulic efficiency. Given data: External diameter (D1) = 1.5 m Internal diameter (D2) = 0.8 m Head on the turbine (H) = 20m Velocity of flow Vf1 = Vƒ2 = 2.8 m/s Guide blade angle α = 12° Runner vanes at inlet radial angle θ = 90° Vwl = u1 Vr1 = Vf1 Discharge is radial Vw2 = u2, V2 = Vƒ2 To find: 1. Speed of the turbine (N) 2. Vane angle at outlet of the runner (ϕ) 3. Hydraulic efficiency (ηh) Solution: Result: 1. Speed at the turbine (N) = 167.68 rpm 2. Vane angle at outlet at me runner ϕ = 21.73 3. Hydraulic efficiency ηh = 88.40% Example - 22 The wheel vanes are radial at inlet and the inlet diameter is twice the outlet diameter. The head available is 11 m and 233 liters of water/sec are supplied to an inward from reaction turbine. The velocity at flow is constant are equal to 1.83 m/s. The wheel makes 370 rpm find. a) Guide vane angle at inlet (b) inlet and outlet dia of the wheel (c) the width of the wheel at inlet and exit, Neglect the thickness of vanes. Assume that the discharge is radial and there is no losses in the wheel. Take speed ratio = 0.7 and inlet vanes are radial. Given data: Discharge (Q) = 233 liters/s = 0.233m3/s Head (H) = 11m Inlet vane radial θ = 90° Vrl = Vƒ1, Vwl = u1 Inlet diameter D1 = 2 × D2 Velocity of flow Vƒ1 = Vƒ2 = 1.83 m/s Speed (N) = 370 rpm Speed ratio = 0.7 To find: (i) Guide vane angle (α) (ii) Inlet and outlet diameter (D1, D2) (iii) Width of the wheel at inlet and outlet Solution: 3. Discharge Q = π D1 В1 Vƒ1 4. From inlet triangle Result: 1. Guide vane angle α = 10.09° 2. Inlet and outlet diameter D1 = 0.532 m, D2 = 0.266 m 3. Width of inlet flow outlet B1 = 0.0762 m, B2 = 0.1524 m 4. Hydraulic efficiency ηh = 97.97% Example - 23 A reaction turbine work at 500 rpm under a head of 130 m. Its diameter at inlet is 110 cm and the flow area is 0.38 m2. The angle by absolute and relative velocities at inlet are 20° and 60° respectively width the tangential velocity. Determine a) Volume flow rate b) The power developed c) Hydraulic efficiency Assume whirl at outlet to be zero Given data: Speed (N) = 500 rpm Inlet diameter (D1) = 110 cm = 1.1m Head (H) = 130 m Flow area = 0.38 m2 Angle made by absolute velocity at inlet α = 20° Angle made by relative velocity at inlet θ = 80° whirl at outlet Vw2 = 0 To find: 1. The volume flow rate 2. Power developed (P) 3. Hydraulic efficiency (ηh) Solution: Result: 1. Volume flow rate (Q) = 5.0388 m3/s 2. Power developed (P) = 52.86.24 Kw 3. Hydraulic efficiency ηh = 82.26% Example - 24 An inward flow reaction turbine developed 1300 Kw power having the vane velocity at inlet as 32 m/sec and the corresponding whirl velocity of 25 m/sec. The ratio of outer to internal diameter is 2. The velocity of flow remaints of 5 m/s. through out and discharge at exit is radial. The head available on the wheel is 90 m find. (1) Vane angles (2) power developed by wheel per unit weight (3) Discharge in m3/s and (4) hydraulic efficiency of turbine. Given data: Power (P) = 1300 Kw = 1300 × 103 w Velocity at wheel u1 = 32 m/s Whirl velocity Vwl = 25 m/s Ratio of diameter D1 / D2 = 2 Velocity of flow Vƒ1 = 5 m/s Head (H) = 90m Discharge is radial Vw2 = 0, β = 90° To find: 1. Vane angle θ, α, ϕ 2. Power developed by wheel/unit weight of water 3. Discharge Q in m3/s 4. Hydraulic efficiency (ηh) Solution: 3. Power developed by wheel / unit weight of water 4. Power (P) = ρQ (Vw1 × u1) 5. Hydraulic efficiency (ηh) Result: 1. Vane angle θ = 144.48°, α = 11.30°, ϕ = 17.35° 2. Power developed by wheel/unit weight of water = 81.54 Nm/N-s 3. Discharge Q = 1.625 m3/s 4. Hydraulic efficiency ηh = 90.61% Example - 25 The following data followed inward flow reaction turbine. Net head = 90 m, Shaft power (S.P) = 400 kw, Hydraulic efficiency ηh = 94%, Speed of the runner N = 700 rpm Flow ratio = 0.17 Overall efficiency η0 = 84% Ratio of wheel width to wheel diameter of inlet = 0.1 Ratio of inlet diameter to outlet diameter = 0.5 Flow velocity constant Discharge radial Find the blade dimensions and blade angles of turbine Given data: Head (H) = 90m Speed (N) = 700 rpm Shaft power (P) = 400 kw = 400 × 103 w Ratio of wheel width to wheel diameter at inlet B1 / D1 = 0.1 Ratio of Inlet diameter to outer diameter D1 / D2 = 0.5 Flow ratio = 0.17 Hydraulic efficiency ηh = 94% Overall efficiency η0 = 84% Flow velocity Vf1 = Vf2 Discharge at radial Vw2 = 0 β = 90° To find: 1. Dimensions of blade 2. Blade angles of turbine Solution: Result: 1. Blade dimensions (i) Inlet diameter D1 = 0.490 m (ii) Outlet diameter D2 = 0.245 m (iii) Inlet Breath B1 = 0.049 m (iv) Outlet Breath B2 = 0.0980 m 2. Vane angles (i) Guide blade at inlet (α) = 8.75° (ii) Vane angle at inlet θ = 14.16° (iii) Vane angle at outlet ϕ = 38.48 Example - 26 In an inward radial flow turbine water enter at an angle of 22° to the wheel tangent to that outer rim and leaves at 3 m/s. The flow velocity is constant through the runner. The inner and outer diameter are 300 mm and 600 mm respectively. The speed of the runner is 300 rpm. The discharge through the runner is radial find (i) Inlet and outlet blade angles (ii) Taking inlet width as 150 mm and neglecting the thickness of the blade. Find the power developed by the turbine. Given data: To Find: 1. Inlet and outlet blade angle θ, ϕ 2. Power developed Solution: 4. Power developed Result: 1. Blade angle θ = 118.99° ϕ = 32.15° 2. Power developed (P) = 59.36 Kw Example - 27 An inward Flow reaction turbine has flow rate of 0.4 m3/s and it works under a head of 35m. The velocity of wheel at inlet is 22 m/s and water discharge through a pipe at exit of 0.34 m diameter in radial direaction. Determine the guide vane angle of inlet, power to turner and hydraulic efficiency velocity of flow remains constant throughout. Given data: Discharge (Q) = 0.4 m3/s Velocity u1 = 22 m/s Head (H) = 35m Diameter of pipe (d) = 0.34m Discharge radial Vw2 = 0 and Vf1 = Vƒ2 = V2 To find: 1. Guide vane angle (α) 2. Power to runner (P) 3. Hydraulic efficiency (ηh) Solution: 1. Discharge Q = Area of pipe × velocity of Flow water at exit 0.4 = π/4 × d2 × Vƒ2 V2 = Vƒ2 3. From inlet velocity triangle 4. Power to runner P = ρQ Vwl × u1 = 1000 × 0.4 × 15.16 × 22 P = 133.408 Kw 5. Hydraulic efficiency Result: 1. Guide vane angle (α) = 16.20° 2. Power to runner (P) = 133.408 Kw 3. Hydraulic efficiency (ηh) = 97.13% Example - 28 A reaction turbine works at 450 rpm under a head of 120 m. Its diameter at inlet is 1.2m and the flow area is 0.4m2. The angles made by absolute and relative velocity at in letare 20° and 60° respectively with the tangential velocity determine. 1. Volume flow rate 2. The power developed 3. Hydraulic efficiency Given data: Speed (N) = 450 rpm Head (H) = 120m Flow area (a) = 0.4m2 Inlet diameter (D) = 1.2m Angle made by absolute velocity α = 20° Angle made by the relative velocity at inlet θ = 60° To find: 1. Volume flow rate (Q) 2. Power developed (P) 3. Hydraulic efficiency (ηh) Solution: Result: 1. Volume flow rate (Q) = 5.211 m3/s 2. Power developed (P) = 5272.4 Kw 3. Hydraulic efficiency (hh) = 85.95% Example - 29 In a veritcal shaft inward flow reaction turbine water enters the runner flow the guide blades at angle of 155° with the runner blade angle of entry being 100°. Both these angle are measured from the tangent at runner periphery, drawn in the direction of runner rotation. The flow velocity through the runner is constant water enters the draft tube from the runner without whirl and the discharge from the draft tube into the railrace takes place with a velocity of 3.0 m/s. The runner has the dimensions of 480 mm external diametor and 45.6 mm inlet width the turbine works with a net head of 50.4 m, and the loss of head in the turbine due to resistance is 5.76m of water. Determine. 1. Speed of the runner 2. Runner blade angle at a point on the outlet edge where the radius of rotation is 108 mm 3. Power generated by the turbine 4. Inlet diameter of the draft tube Given data: External diameter (D1) = 480mm = 0.48m Inlet width of the runner (B1) = 45.63mm = 0.0456m Head (H) = 50.4m Loss of head in the turbine = 5.76m Absolute velocity at exit V2 = 3 m/s Outlet raduis (R2) = 108 mm = 0.108m To find: 1. Speed of the runner (N). 2. Runner blade angles. 3. Power generated by the turbine. 4. Inlet diameter of the draft tube. Solution: 1. From inlet velocity triangles (i) α = 180° - 155 α = 25° (ii) θ = 180° - 100 θ = 80° 2. Net Head (H) = workdone + kinetic head at exit + Losses in that runner 4. From outlet velocity triangle 5. Discharge (Q) = πD1 В1 Vƒ1 = π × 0.48 × 0.0456 × 10.14 Q = 0.697 m3/s 6. Vwl = 2.144 × Vƒ1 = 2.144 × 10.14 Vwl = 21.740 m/s 7. Power generated (P) = ρQ Vwl u1 = 1000 × 0.697 × 21.740 × 19.95 = 302.2×103 w P = 302.2 Kw Result: 1. Speed of runner (N) = 794 rpm 2. Runner blade angle at outlet (ϕ) = 48.5° 3. Power generated (P) = 302.2 Kw 4. Inlet diameter of draft tube (d) = 0.295m Example - 30 An inward flow reactin turbine operating under 30m head develope 4000 Kw while running at 300 rpm. The over all efficiency of the turbine is 0.85 and hydraulic efficiency is 0.90 and radial velocity of flow at inlet is 7 m/s. The inlet guide vane angle at full gate opening is 30o. Calculate the diameter and width of the runner at inlet Blade thickness coefficient 5% Given data: Head (H) = 30m Power (P) = 4000 Kw = 4000 × 103 w Speed (N) = 300 rpm Overall efficiency η0 = 0.85 Hydraulic efficiency ηh = 0.90 Flow velocity Vƒ1 = 7m/s Vane thickness coefficient (Kt) = Guide angle (α) = 30° To find: 1. Diameter of the runner at inlet (D1) 2. Width of the runner at inlet (B1) Solution: Result: 1. Inlet diameter (D1) = 1.39m 2. Width of inlet (B1) = 0.55m
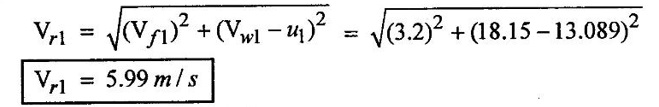

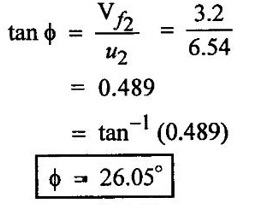
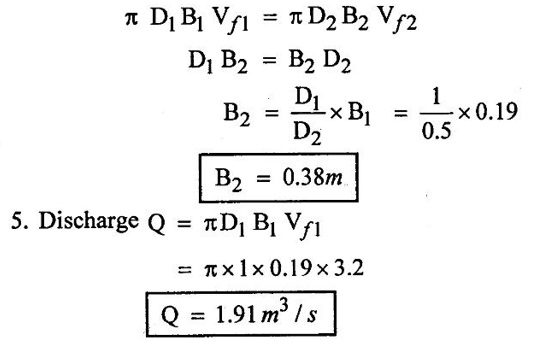
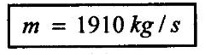


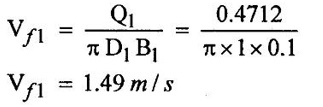
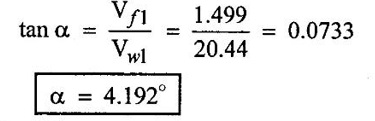
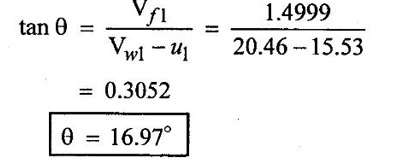
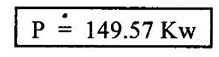

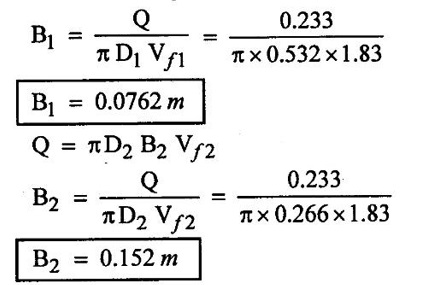


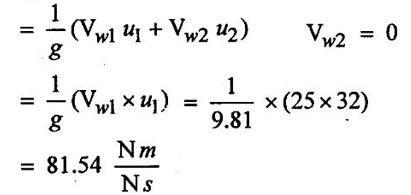
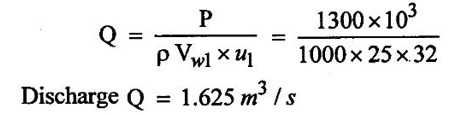

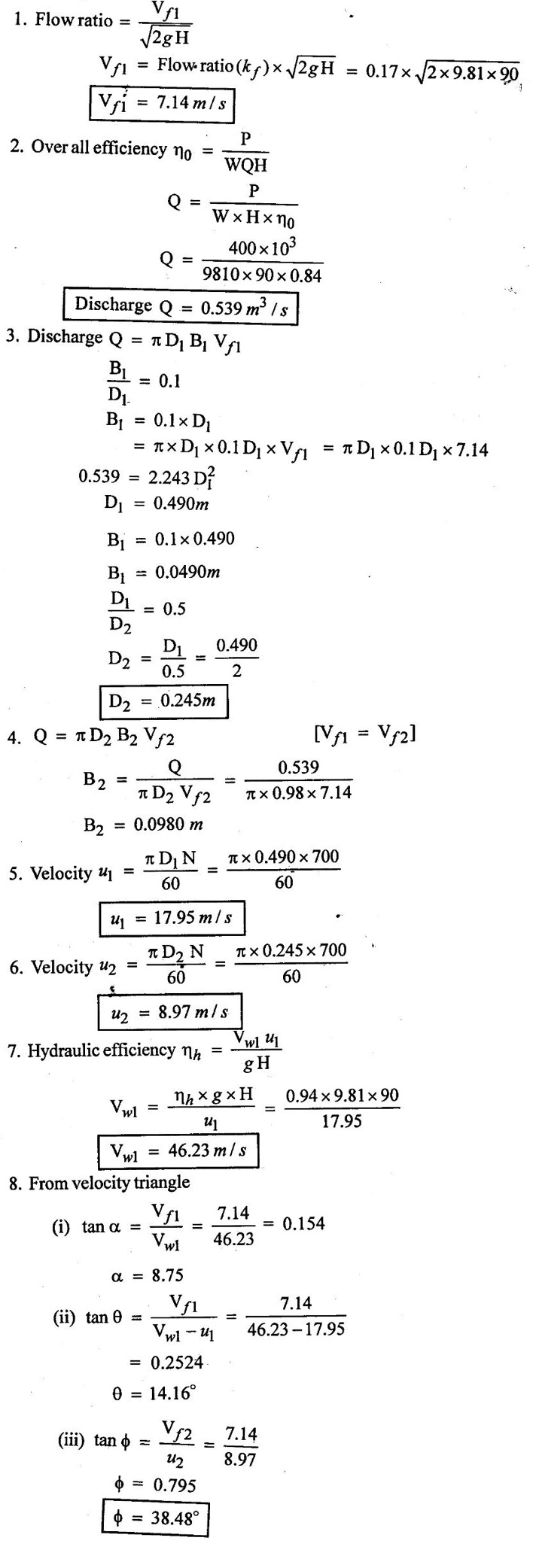


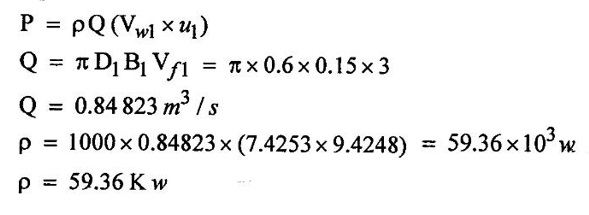
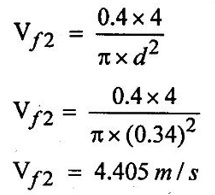
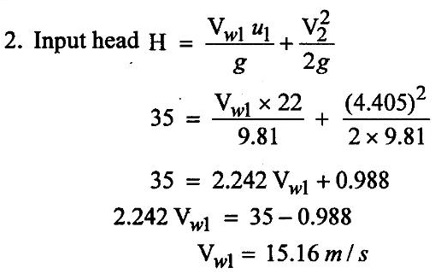
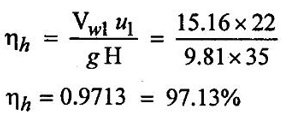


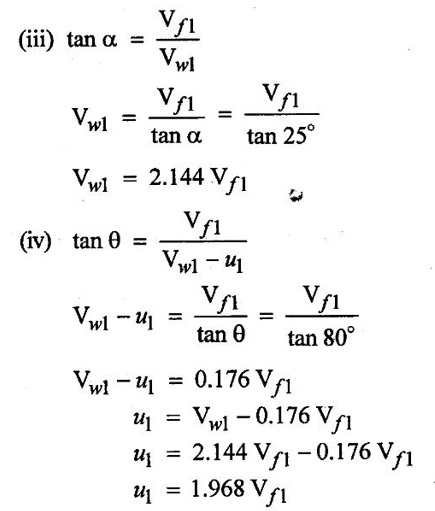

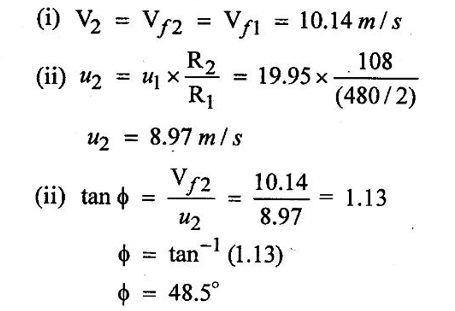
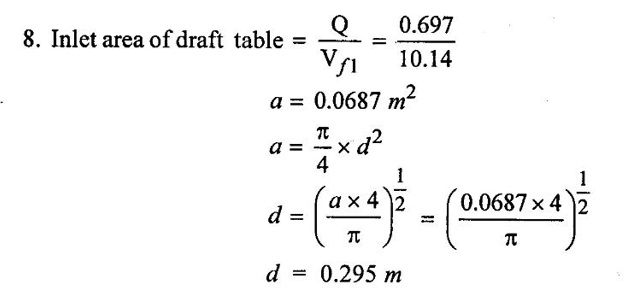
 = 0.95
= 0.95
Fluid Mechanics and Machinery: Unit 4: Turbines : Tag: : - Solved Examples based on inward flow reaction turbine
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
