Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics
Solved Examples Based on Continuity Equation
Fluid Mechanics
Solved Examples Based on Continuity Equation : Examples: Fluid Mechanics and Machinery: Fluid Properties and Flow Characteristics
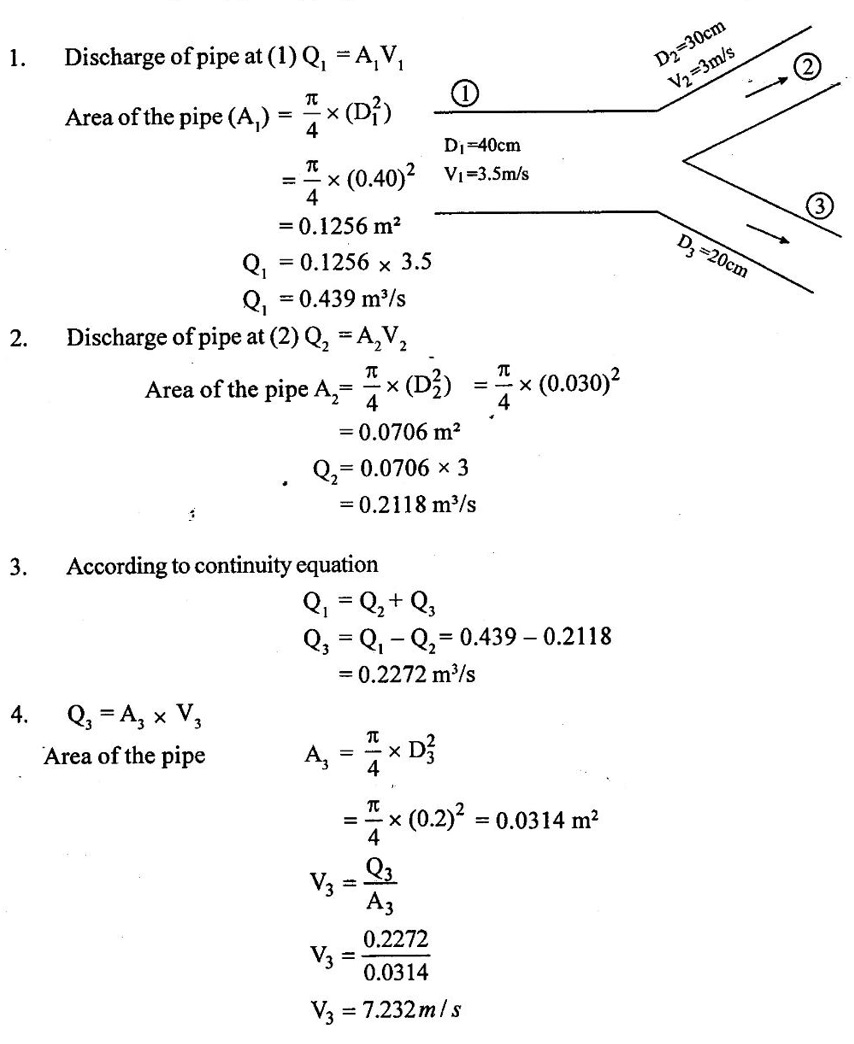
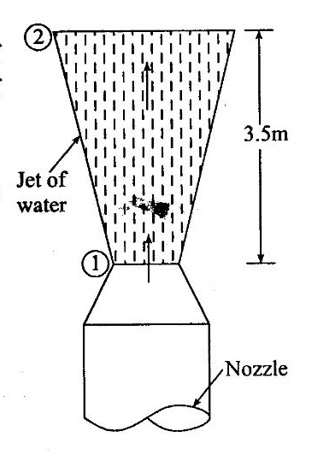
SOLVED EXAMPLES BASED ON CONTINUITY EQUATION Example - 47 The diameter of a pipe of the sections 1 and 2 are 15cm and 20 cm respectively. Find the discharge through the pipe if the velocity of water flowing through the pipe of section (1) is 10 m/s and also determine velocity at section (2) Given data: Section (1) Diameter of the pipe (D1) = 15 cm Velocity of the pipe (V1) = 10 m/s Section (2) Diameter of the pipe (D2) = 20 cm To find: 1) Discharge through the pipe (Q) 2) Velocity of flow (V2) at section (2) Solution: 1. Discharge through the pipe (Q) = A1V1 = 0.01767 m2 Q = 0.01767 × 10 Q = 0.1767 m3/s 2. According to continuity equation A1V1 = A2V2 V2 = A1V1 / A2 A2 = 0.0314 m2 V2 = 0.01767 × 10/0.0314 V2 = 5.624 m/s Result : (i) Q = 0.1767 m3/s (ii) V2 = 5.624 m/s Example - 48 Water is flowing through a horizontal tapered pipe. The diameter of larger end is 250 mm and the diameter at smaller end is 100mm. The velocity of water at largest end is 3 m/s. Determine a) The velocity head at smaller end b) The velocity head at larger end c) The discharge through the pipe Given data: Diameter of larger end D1 = 250 mm = 0.25 m Diameter of smaller end D2 = 100 mm = 0.1 m Velocity at larger end V1 = 3 m/s To find: a) The velocity head (V12/2g) at larger end b) The velocity head (V22/2g) at smaller end c) Discharge through the pipe (Q) Solution : = 0.0490 m2 = 7.85 × 10-3m2 3. According to continuity equation A1V1= A2V2 V2 = A1V1/A2 = 0.0490 × 3/7.85 × 10-3 V2 = 18.73 m/s 4. Velocity head at larger end = V12/2g = 32/2 × 9.81 = 0.4587 m/s 5. Velocity head at smallest end = V22/2g = 18.732/2 × 9.81 = 17.88 m/s 6. Discharge through pipe (Q) = A1V1 = A2V2 Q = A1V1 = 0.0490 × 3 Q = 0.147 m3/s Q = 147 liters/s Result : (i) Velocity head at larger end = V12/2g = 0.4587 m/s (ii) Velocity head at smallest end = V22/2g = 17.88 m/s (iii) Discharge through pipe (Q) = 147 litres/s Example - 49 The diameter of a pipe at 40 cm conveying water into two pipes of diameter 30 cm and 20 cm respectively. If the average velocity in the 40 cm diameter pipe is 3.5 m/s. Find the discharge in this pipe. Also determine the velocity in 20 cm pipe, if the average velocity in 30 cm diameter pipe is 3 m/s. Given data: Diameter of pipe at (1) D1 = 40 cm = 0.4 m Velocity of the pipe at (1) V1 = 3.5 m/s Diameter of pipe at (2) D2 = 30 cm= 0.3 m Velocity of the pipe at (2) V2 = 3 m/s Diameter of pipe at (3) D3 = 20cm = 0.2 m To find: 1) Discharge of pipe at (1) Q1 2) Velocity of the pipe at (3) V3 Solution : Result: (i) Discharge of pipe (Q1) = 0.439 m3/s (ii) Velocity of pipe at (3) V3 = 7.232 m/s Example - 50 Water flow throw a pipe AB 1.3m diameter at 4m/s and then passed through a pipe BC 1.8m diameter. At C the pipe branched. Branch CD is 0.6m and carries one-fourth of the flow in AB. The flow velocity in branch CE is 2.8m/s. Find the rate of flow in AB, Velocity in BC, velocity in CD and diameter of CE. Given data: Diameter of pipe AB (DAB) = 1.3m Velocity of pipe AB (VAB) = 4m/s Diameter of pipe BC (DBC) = 1.8m Diameter of pipe CD (DCD) = 0.6m Velocity of pipe CE (VCE) = 2.8m/s Rate of flow of pipe CD (QCD) = ¼ (QAB) To Find: i. Rate of flow of pipe AB (QAB) ii. Velocity of pipe BC (VBC) iii. Velocity of pipe CD (VCD) iv. Diameter of pipe CE (DCE) Solution : Result: (i) Rate of flow of pipe AB (QAB) = 5.308 m3/s (ii) Velocity of pipe BC (VBC) = 2.086 m/s (iii) Velocity of pipe CD (VCD) = 4.70 m/s (iv) Diameter of pipe CE (DCE)=1.345 m Example - 51 A 30cm diameter pipe carries oil of specific gravity 0.8 at a velocity 4m/s. At another section the diameter is 25cm. Find the velocity of this section and also mass rate of flow of oil. Given data: i. Diameter of pipe at section −1 (D1) = 30cm = 0.3m ii. Velocity of the pipe at section -1 (V1) = 4m/s iii. Diameter of pipe at section − 2 (D2) = 25 cm = 0.25m iv. Specific gravity of oil (s) = 0.8 To Find: i. Velocity of section at section -2 ii. Mass flow rate of oil Solution : Result: (i) Velocity at section (2) V2 = 5.759 m/s (ii) Mass flow rate (m) = 225.92 kg/s Example - 52 A jet of water from a 35mm diameter nozzle is directed vertically upwards. Assuming that the jet remains circular and neglecting any loss of energy. Determine the diameter of the jet at a point 3.5m above the nozzle, if the velocity with which the jet leaves the nozzle is 10m/s. Given data: Dia of nozzle at point (1) (D1) = 35mm = 0.035m Velocity of jet nozzle at point (2) (V1) = 10 m/s Height (h) at point (2) = 3.5 m To find: Diameter of jet (D2) at a point (2) height of 3.5 m Solution: Consider upward motion of the jet from the outlet of the nozzle point (1) to the point (2) (neglecting any loss of energy) Initial Velocity (V1) = 10m/s Acceleration due to Gravity (g) = -9.81m/s2 (due to upward motion) Using relation V22 – V12 = 2gh V22 = 2gh + V12 Result: Diameter of jet (D2) at point (2)=0.0467 m Example - 53 Water flows steadily into a cylindrical tank of diameter 0.60m through a 60 mm diameter pipe at 6m/s and leaves through two pipes of diameter 40mm and 50mm at 2.5 m/s and 3m/s respectively. The tank roof has a 50mm diameter vent allowing flow of air. Find the rate of change of water level in the tank and the velocity of air flow through the vent. Assume all flows to be incompressible. Given data: Inlet pipe at -1 Diameter (d1) = 65mm = 0.065m Velocity (V1) = 6m/s Outlet pipe at - 2 Diameter (d2) = 40mm = 0.040m Velocity (V2) = 2.5m/s Outlet pipe at - 3 Diameter (d3) = 60mm = 0.060m Velocity (V3) = 3m/s Cylindrical diameter of tank (D) = 0.60m Tank roof diameter (da) = 50mm = 0.050m To find: i. Rate of change of water level in the tank ii. Velocity of air through the vent Solution: (i) Entry of fluid = outlet of fluid in the tank [According to continuity equation] Rate of flow in pipe (Q1) at 1 = Rate of flow in pipe (Q2) at 2 + Rate of flow in pipe (Q3) at 3 + Rate of change of water in the tank (Q). A1V1 = A2V2 + A3V3 + A × dh / dt Result: (i) Rate of change of water level in the tank (dh/dt) = 0.0676 m/s (ii) Velocity of air through the vent (V4) = 0.09734 m/s.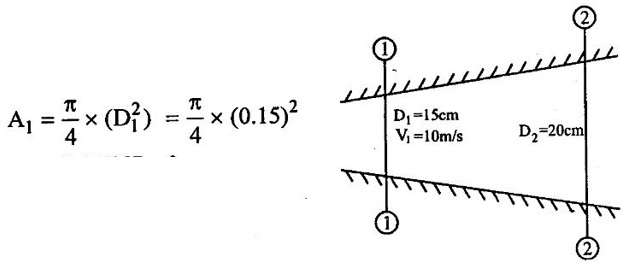
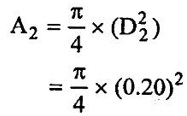

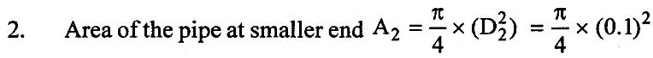




Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics : Tag: : Fluid Mechanics - Solved Examples Based on Continuity Equation
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
