Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics
Solved Examples Based on Bernoullis Equation for Real Fluid
Fluid Mechanics
Solved Examples Based on Bernoullis Equation for Real Fluid: Fluid Properties and Flow Characteristics - Fluid Mechanics and Machinery
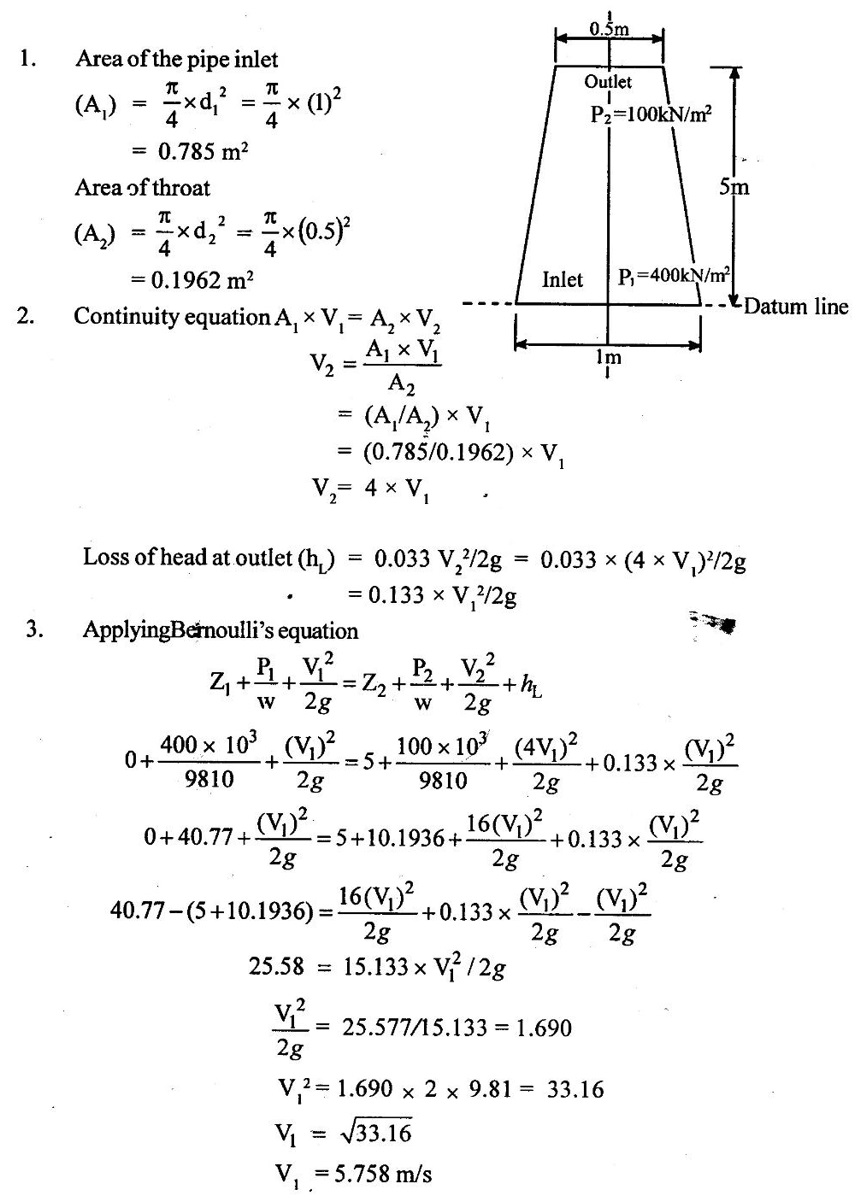
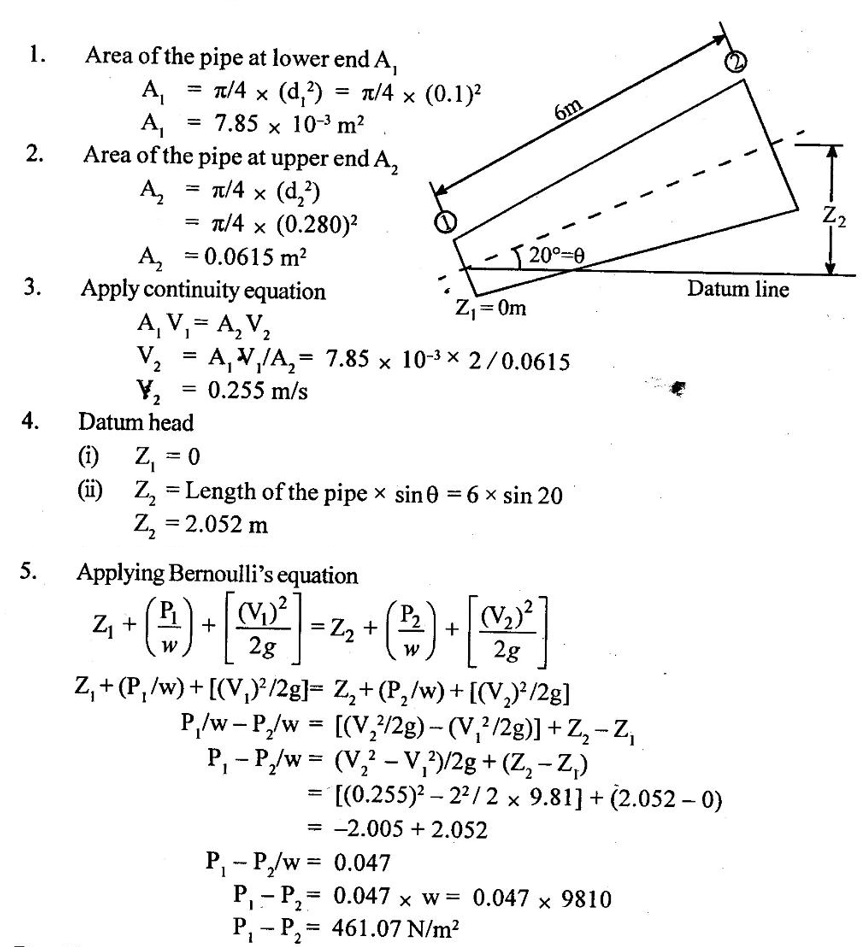
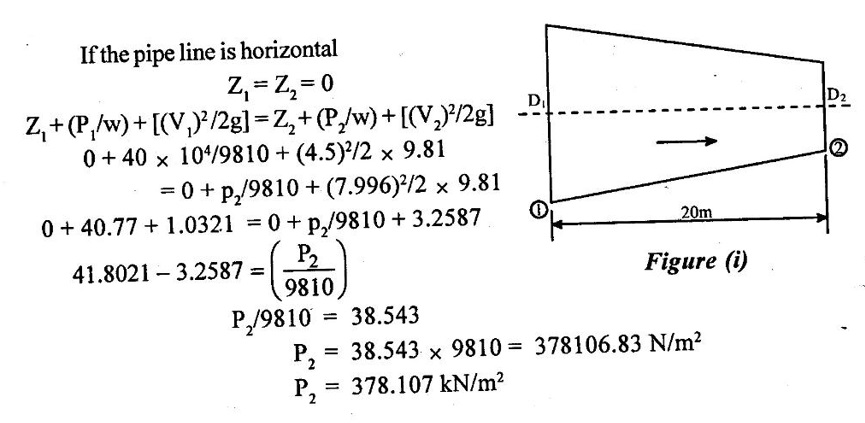
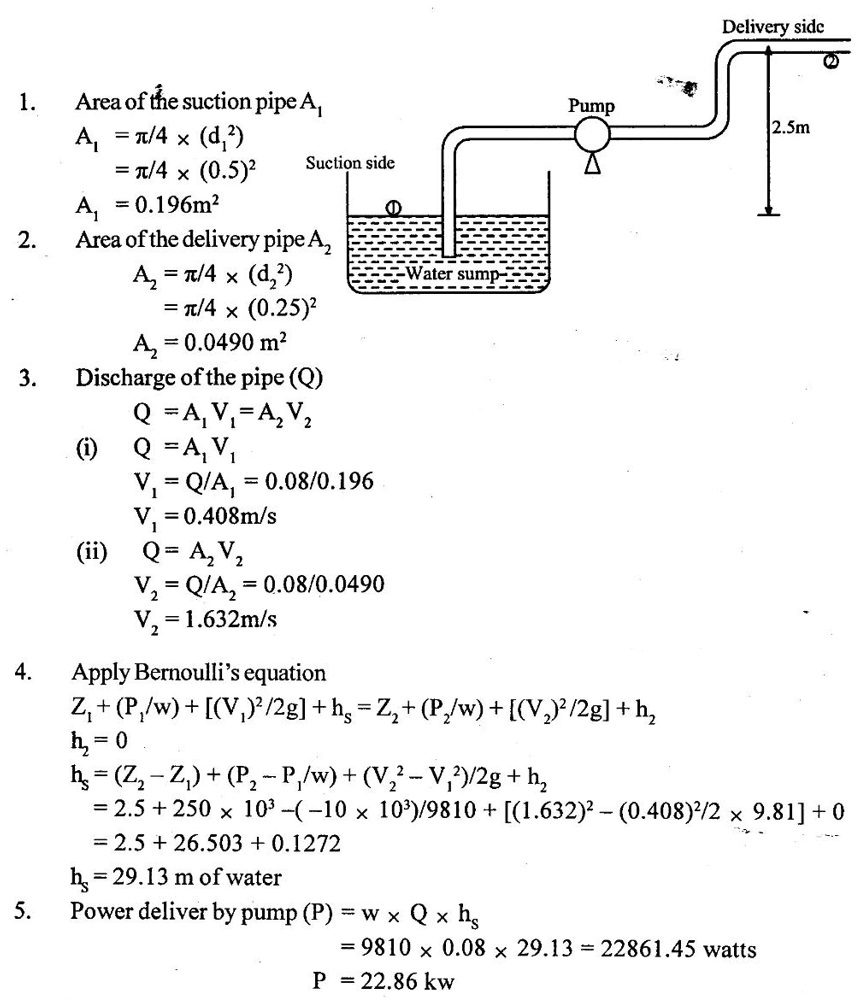
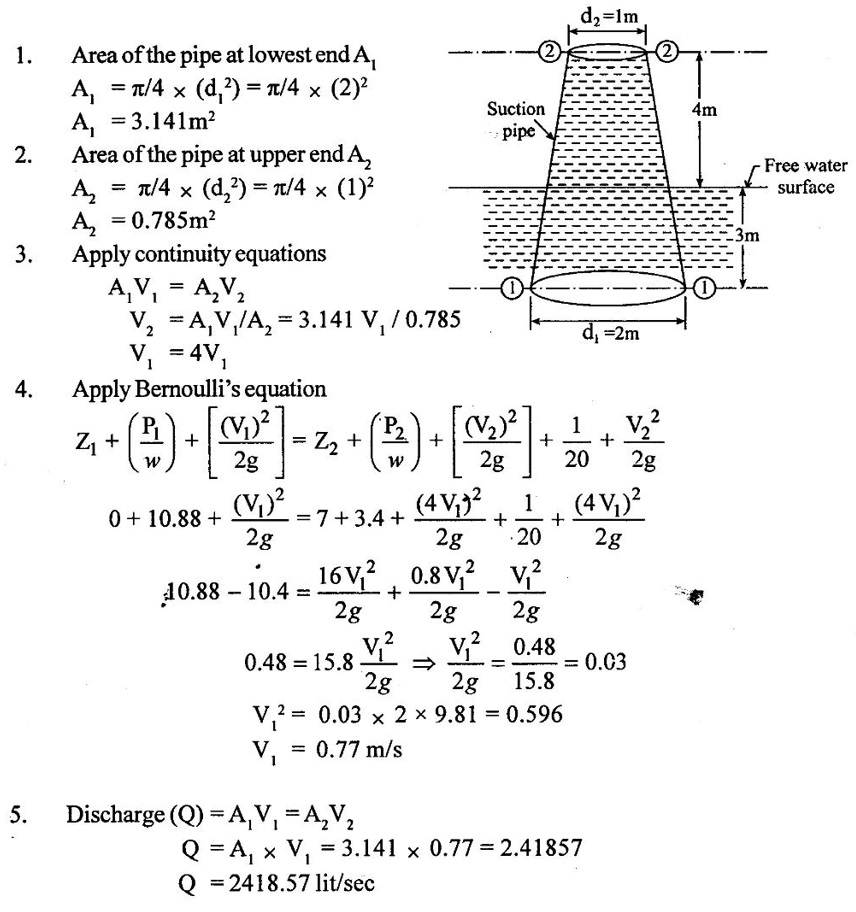
SOLVED EXAMPLES BASED ON BERNOULLIS EQUATION FOR REAL FLUID Example - 60 A pipe of diameter 500mm carries water at a velocity of 30m/s, the pressure at point A and B are given 250 kpa and 200 kpa respectively. While the datum head at A and B are 28 m and 20 m respectively. Find the loss of head between A and B. Given data: Diameter (d) = 500mm Velocity (V) = 30m/s At a point A, Pa = 250 kpa = 250KN/m2 = 250 × 103 N/m2 Za = 28 m Va = V At a point B, Pb = 200kpa 200KN/m2 = 200 × 103 N/m2 Zb = 20 m Vb = V To find: Loss of energy (h1) Solution : Result : Loss of energy (h1) = 13.093m Example - 61 A conical tube of length 3 m is fixed vertically with its smaller end upwards. The velocity of flow at the smaller end is 6 m/s while the lower end is 3 m/s. The pressure at the smaller end is 3.5m of liquid. The loss of head in the tube is Given data: Length of the tube, (L) = 3m Velocity of smaller end (V1) = 6m/s Pressure head at the smaller end (P1/ρg) = 3.5m of the liquid Velocity of lower end (V2) = 3m/s To find: Pressure head at lower end Solution: Result : Pressure head at lower end (P2/w) = 7.394 m of fluid. Example - 62 A pipe line carrying oil of specific gravity 0.91, changes in diameter from 300 mm diameter at a position A to 600 mm at a position B which 5 m at higher level. If the pressure at A and B are 10.46 N/cm2 and 6.886 N/cm2 respectively and the discharge is 300 lit/sec. Determine the direction of flow and loss of head. Given data: Specific gravity of oil (s) = 0.91 At point A Diameter (da) = 300mm = 0.3m Pressure (Pa) = 10.46N/cm2 = 10.46 × 104N/m2 Assume (Za) = 0 At a point B Diameter (db) = 600mm = 0.6m Pressure (Pb) = 6.886N/cm2 = 6.886 × 104N/m2 Datum level (Zb) = 5m Discharge (Q) = 300lit/sec = 0.3m3/s To find: (i) Direction of flow (ii) Loss of head (H) Solution: Specific weight of water (w) = 9810 N/m3 = 0 + 10.662 + 0.920 = 11.582m 6. Direction of flow Total energy at point A (Ha) < total energy at point B(Hb) Hence flow is taking place from B to A 7. Loss of head (H) H = Hb – Ha = 12.076 - 11.582 = 0.494 m Result : (i) Flow is taking place from B to A. (ii) Loss of head (H) = 0.494 m. Example - 63 A tapered section pipe is running full of water. The diameter of the pipe at inlet and outlet are 1.0 m and 0.5 m respectively. The outlet is at a vertical height of 5 m above the inlet. The loss of head in the pipes is 1/30 of the velocity head at outlet. The pressure at the outlet section is 100 kN/m2 whereas at the inlet is 400 kN/m2. Calculate the rate of discharge through the pipe. Given data: At section 1: Inlet Diameter (d1) = 1.0m Pressure (P1) = 400kN/m2 = 400 × 103N/m2 At section 2: Outlet Diameter (d2) = 0.5m Pressure (P2) = 100kN/m2 = 100 × 103N/m2 Loss of head (h1) = (1/30) × V22/2g = 0.033 V22/2g Datum head (Z2) =5m To find: The rate of discharge (Q) Solution: 4. Velocity at outlet (V2) = 4 × V1 = 4 × 5.758 = 23.032 m/s 5. Discharge (Q) = A1 × V1 = A2 × V2 Q = A1 × V1 = 0.785 × 5.758 = 4.52 m3/s. Result : Discharge (Q) = 4.52 m3/s. Example - 64 A pipe slope down in 1 in 100 and upper from 0.30m diameter to 0.20m diameter at lower end. If the pipe carries 100 lps of oil specific gravity 0.80. calculate pressure at the lower end. The length of the pipe is 200m and the upper end gauge reads 60 kpa. Length of the pipe is (L) = 200m Slope of the pipe = 1 in 100 Specific gravity of oil (S) = 0.80 Upper end at pipe section (1) Diameter of the pipe(d1) = 0.30m Pressure of the pipe (P1) = 60kpa = 60 × 103 Pa = 60 × 103 N/m2 [1 Pa = 1 N/m2] Lower end at pipe section (2) Diameter of the pipe (d2) = 0.20m Discharge (Q) = 100 lps = 0.1m3/s To find: Pressure of the lower end (P2) Solution: (ii) Q = A2V2 V2 = Q/A2 = 0.1/0.0314 V2 = 3.185 m/s 4. Datum head (i) Z1 = Slope × length of the pipe = 1/100 × 200 Z1 = 2m (ii) Z2 = 0 5. Specific gravity of oil (S) = density of oil/ density of water Density of oil = S × density of water = 0.8 × 1000 ρoil = 800 kg/m3 6. Specific weight of oil w = ρoil × gravity g = 800 × 9.81 = 7848 N/m3 7. Applying Bernoulli's equation. 2 + 7.645 + 0.1019 = 0 + P2/7848 + 0.517 9.7469 = (P2/7848) + 0.517 9.7469 - 0.517 = P2/7848 P2 = 9.2299 × 7848 P2 = 72436.25 N/m2 P2 = 72.436 kN/m2 P2 = 72.436 kPa Result : P2 = 72.436 kPa. Example - 65 A 6 m long pipe is inclined at an angle of 20° with the horizontal. The smallest section of the pipe which is at a lowest level is 100 mm diameter and the largest section of the pipe is 280mm diameter. Determine the difference of pressure between the 2 sections if the pipe is uniformly tapering and the velocity of the water of the smallest end is 2m/s Given data: Length of the pipe (L) = 6 m pipe incline d(θ) = 20° Lower or smallest end Diameter of the pipe (d1) = 100 mm = 0.1 m Velocity of the pipe (V1) = 2 m/s Upper or highest end Diameter of the pipe (d2) = 280 mm = 0.28 m To find: Pressure difference between the two sections (P1 - P2) Solution: Result : P1 - P2 = 461.07 N/m2 Example - 66 At a point in a pipe line where the diameter is 20 cm the velocity of the water is 4.5 m/s and the pressure is 40 N/cm2. At a point 20 m downstream in the diameter reduces to 15cm. Calculate the pressure of downstream side if the pipe line is (1) horizontal (2) vertical with flow down water (3) vertical with flow upward Given data: Pipe at largest end or upstream side Diameter of the pipe (d1) = 20 cm = 0.2 m Velocity of the pipe (V1) = 4.5 m/s Pipe of the smallest or downstream side Length of the pipe = 20 m Diameter of the pipe (d2) = 15 cm = 0.15 m Pressure of the largest end (P1) = 40 N/cm2 = 40 × 104 n/m2 To find: Pressure of the downstream side or smallest end when (i) Pipe is horizontal (ii) Pipe is vertical with flow downwards (iii) Pipe is vertical with flow upwards Solution: 1. Area of the pipe at largest end A1 = π/4 × (d12) = π/4 × (0.20)2 = 0.0314m2 2. Area of the pipe at smallest end A2 = π/4 × (d22) = π/4 × (0.15)2 = A2 = 0.01767m2 3. Apply continuity equation A1V1 = A2V2 V2 = A1 V1/A2 = 0.0314 × 4.5/0.01767 V2 = 7.996 m/s Case 1: Case 2: Case (3): Result : (i) P2 = 378.107 kN/m2 when the pipeline is horizontal. (ii) P2 = 574.31 kN/2 when the pipeline vertical with flow downwards. (iii) P2 = 181.91 kN/m2 when the pipeline vertical with flow up water. Example - 67 The pressure difference between suction and delivery side of the pump is 200 mm of water column. The suction and delivery pipe diameters are 200 mm and 100 mm respectively. Flow rate is 200 litres/second. Assume losses are negligible. Calculate the power delivery by pump to the water. Given data: The pressure head difference (P2 - P1/w) = 200mm = 0.2m of water column Suction pipe diameter d1 = 200mm = 0.2m Delivery pipe diameter d2 = 100mm = 0.1m Discharge of the pump (Q) = 200 lit/sec = 0.2 m3/sec To find: Power delivery by pump Solution: 1. Area of the suction pipe A1 А1 = π/4 × (d12) = π/4 × (0.2)2 A1 = 0.0314 m2 2. Area of the delivery pipe A2 A2 = π/4 × (d22) = π/4 × (0.1)2 A2 = 0.00785m2 3. Discharge (Q) Q = A1V1 = A2V2 (i) Q = A1 V1 V1 = Q/A1 = 0.20/0.0314 V1 = 6.369 m/s (ii) Q = A2V2 V2 = Q/A2 = 0.20/0.00785 V2 = 25.478 m/s 4. Apply Bernoulli's equation for pump Z1 + (P1/w) + [(V1)2/2g] = Z2 + (P2/w) + [(V2)2/2g] loss of head hd = 0 [Losses are negligible] assume Z1 = Z2 = 0.2 + 31.017 hs = 31.217 m 5. Power delivery by pump to water P = w × Q × hs = 9810 × 0.2 × 31.217 P = 61247.75 watts Result : Power delivery by pump (P) = 61247.75 watts Example - 68 The water is drawn from reservoir through a suction pipe 500 mm diameter by a pump that discharges into delivery pipe of 250 mm diameter. The suction pipe pressure gauge shows a reading of pressure -10 kpa while the pressure gauge on the discharge side reads an absolute pressure of 250 kpa. Discharge rate is 0.08 m3/s, the vertical height between the inlet pressure gauge and exit pressure gauge is 2.5m. Calculate power delivered by pump to the water and losses are negligible. Given data: Diameter of the suction pipe (d1) = 500 mm = 0.5 m Diameter of the delivery pipe (d2) = 250 mm = 0.25 m Suction pipe pressure (P1) = −10 kpa = −10 × 103N/m2 Delivery pipe pressure (P2) = 250 kpa = 250 × 103N/m2 Height difference between pressure gauge (Z2 – Z1) = 2.5 m Discharge (Q) = 0.08 m3/sec To find: Power delivered by pump Solution: Result : Power (P) = 22.86 kw. Example - 69 A pipe is 20 cm in diameter and is at an elevation of 200m at section 1. At section 2 it is at an elevation of 110m and has a diameter of 40 cm . When a discharge of 70 l/s of water is passed through this pipe, the pressure of section 1 is 50 kpa . The energy losses or loss of head in the pipe is 3m. Calculate the pressure of B when the flow is (A) from section (1) to (2), (B) from section (2) to (1). Given data: Pipe diameter at section 1 (d1) = 20 cm = 0.2 m Datum head at section 1 (Z1) = 200 m Pipe diameter at section 2 (d2) = 40 cm = 0.4 m Datum head at section 2 (Z2) = 110 m Pressure at section 1 (P1) = 50 kpa = 50 × 103 N/m2 Loss of head in the pipe (hL) = 3 m Discharge at section 1 (Q)= 70 l/s = 0.070 m3/s To find: Pressure at section 2 when A Flow from section (1) to (2) B Flow from section (2) to (1) Solution: 1. Area of the pipe at section 1 (A1) А1 = π/4 × (d12) = ́π/4 × (0.2)2 A1 = 0.0314m2 2. Area of the pipe at section 2 (A2) А2 = π/4 × (d22) = π/4 × (0.4)2 A2 = 0.1256m2 3. Discharge of the pipe (Q) Q = A1V1 = A2V2 (i) Q = A1 V1 V1 = Q/A1 = 0.070/0.0314 V1 = 2.229m/s (ii) Q = A2V2 V2 = Q/A2 = 0.70/0.1256 V2 = 0.557 m/s 4. Total energy at section 1 (E1) = 200 + 5.096 + 0.253 E1 = 205.34m 5. Total energy at section 2 (E2) E2 = Z2 + (P2/w) + [(V2)2/2g] = 110 + P2/w + (0.557)2/2 × 9.81 = 110 + P2/w + 0.0158 E2 = 110.015 + P2/w 6. Flow from 1 to 2 E1 > E2 E1 - E2 = loss of head (h2) E1 - E2 = 3m 205.34 - (110.015 + P2/w) = 3 205.34 - 113.0158 = P2/w P2 = 92.325 × 9810 P2 = 905708.25 N/m2 7. Flow from 2 to 1 E2 > E1 E2 - E1 = 3m 110.015 + P2/w - 205.34 = 3 P2/w = 3 + 205.34 – 110.015 P2/w = 98.325 P2 = 98.325 × 9810 P2 = 964568.25 N/m2 Result : (A) Flow from 1 to 2 (P2) = 905708.25 N/m2 (B) Flow from 2 to 1 (P2) = 964568.25 N/m2 Example - 70 The drainage pump has tapered suction pipe. The pipe is running full of water. The pipe diameter of the inlet (or) lower end and the outlet (or) upper end are 2m and Im respectively. The free water surface is 3m above the center of the inlet and center of the upper end is 4 m above the top of free water surface. The pressure at top end of the pipe is 25 cm of mercury and lowest end of the pipe is 80 cm of mercury. The loss of head by friction between top and bottom section is 1/20 of the velocity of head of the top section. Compute the discharge in l/s neglect the loss of head of the entrance of the tapered pipe. Given data: Inlet or lowest end of pipe 1 Diameter d1 = 2m Pressure head P1/w = 80cm of mercury = 80/100 × 13.6 = 10.88 m of water Outlet or upper end of the pipe 2 Diameter d2 = 2m Pressure head p2/w = 25cm of mercury = 25/100 × 13.6 = 3.4 m of water Datum head of lowest end Z1 = 0 Datum head at highest end Z2 = 3 + 4 = 7m To find: Discharge of the pipe Q in l/s Solution: Result : Discharge (Q) = 2418.57 lit/sec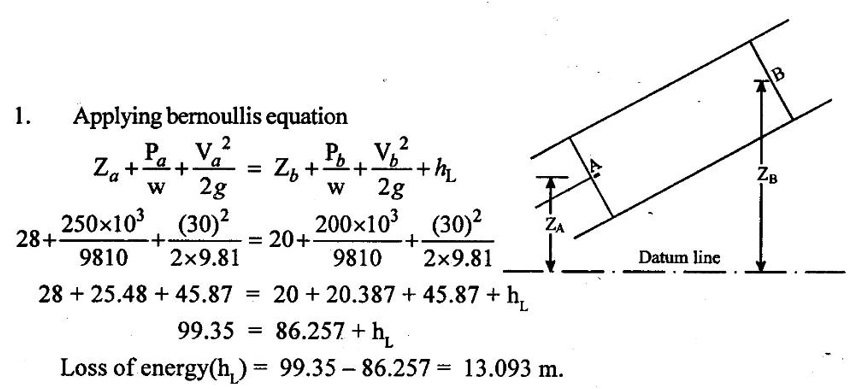
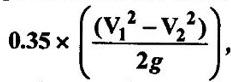 where V1 is the velocity at smaller end and V2 at the lower end respectively. Determine the pressure head at lower end if flow takes place in the downward direction.
where V1 is the velocity at smaller end and V2 at the lower end respectively. Determine the pressure head at lower end if flow takes place in the downward direction.
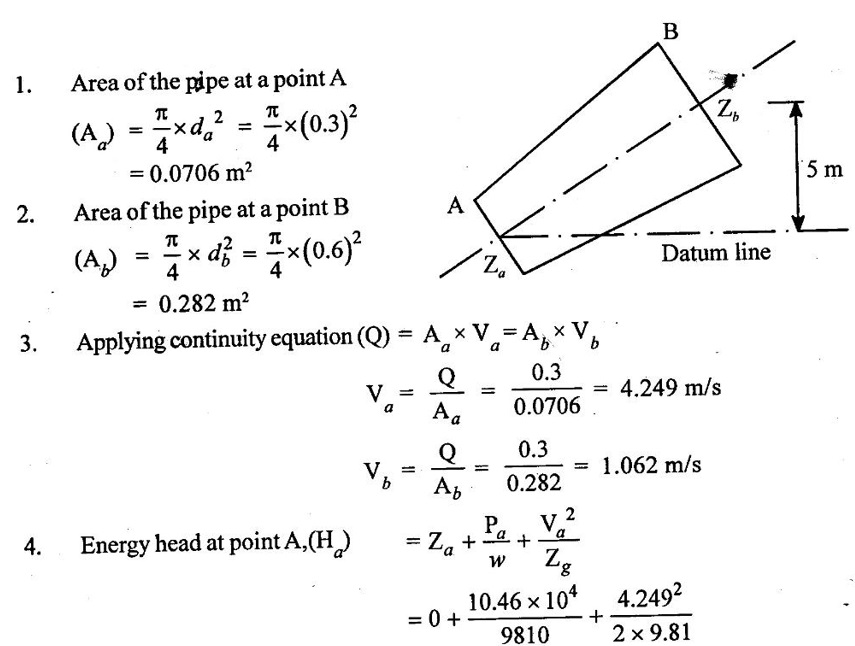
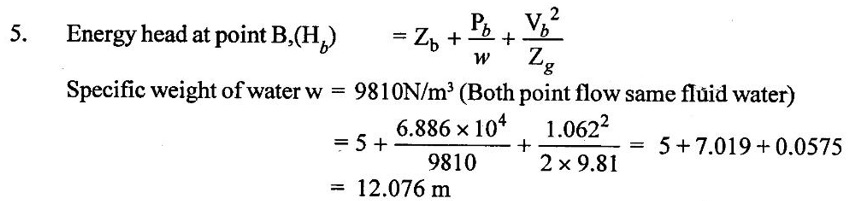
Given data: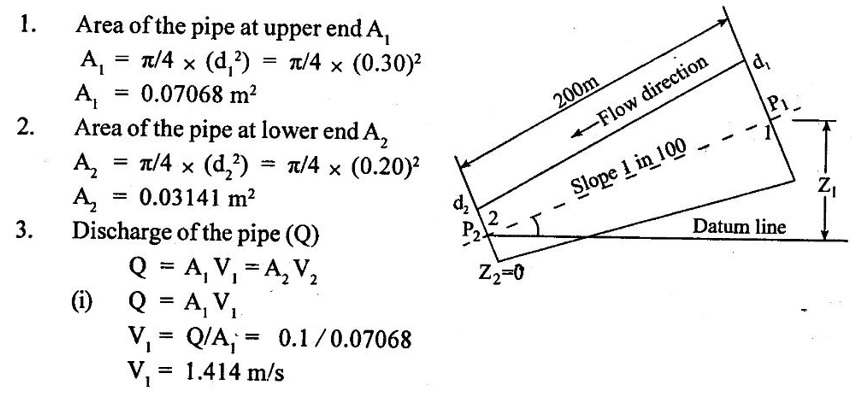
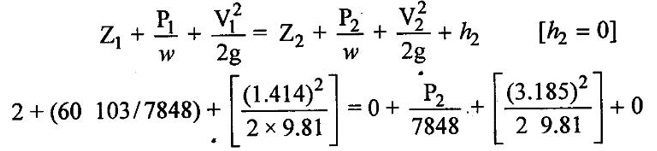


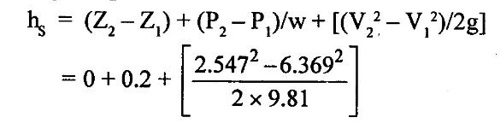

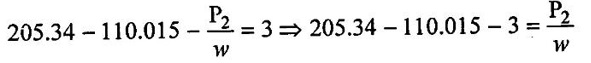
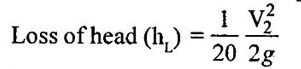
Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics : Tag: : Fluid Mechanics - Solved Examples Based on Bernoullis Equation for Real Fluid
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
