Engineering Mechanics: Unit III: Distributed Forces
Solved Example & Practice Problems: Moment of Inertia of Composite Areas
Solved Example Problems, Examples for Practice: Moment of Inertia of Composite Areas - Distributed Forces - Engineering Mechanics
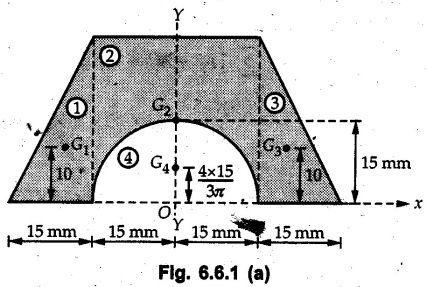
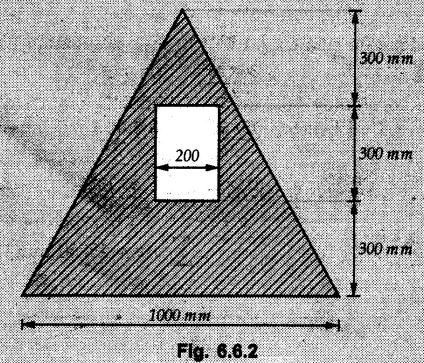
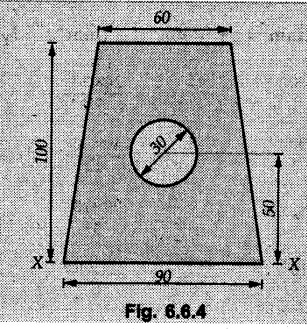
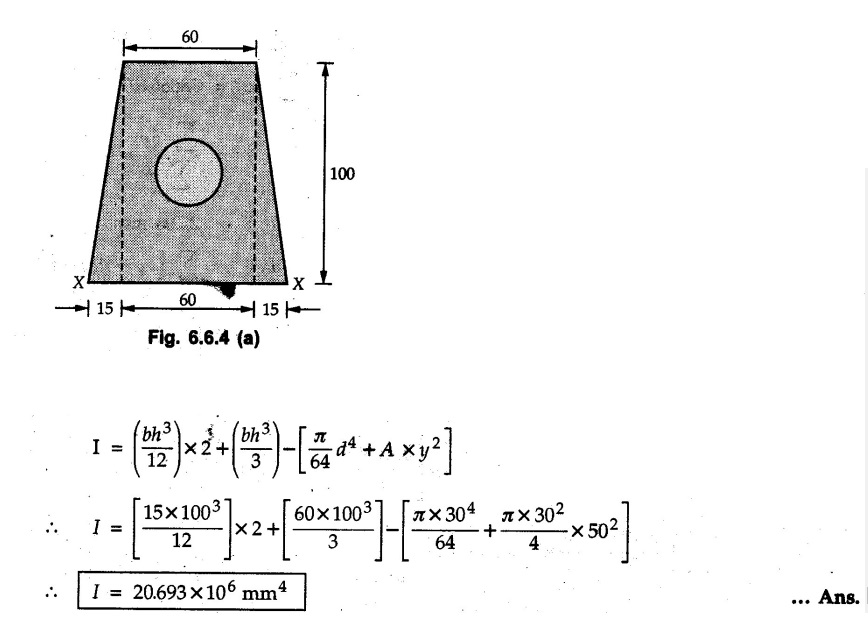
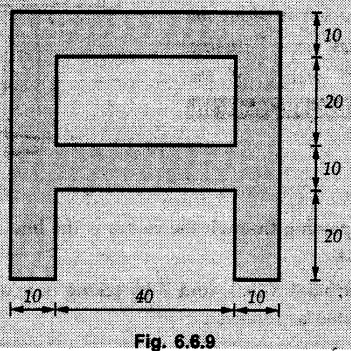
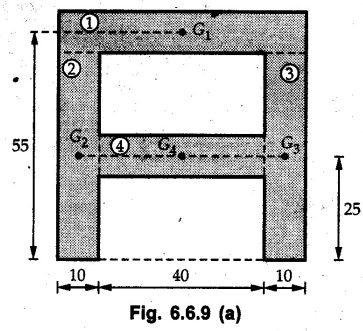
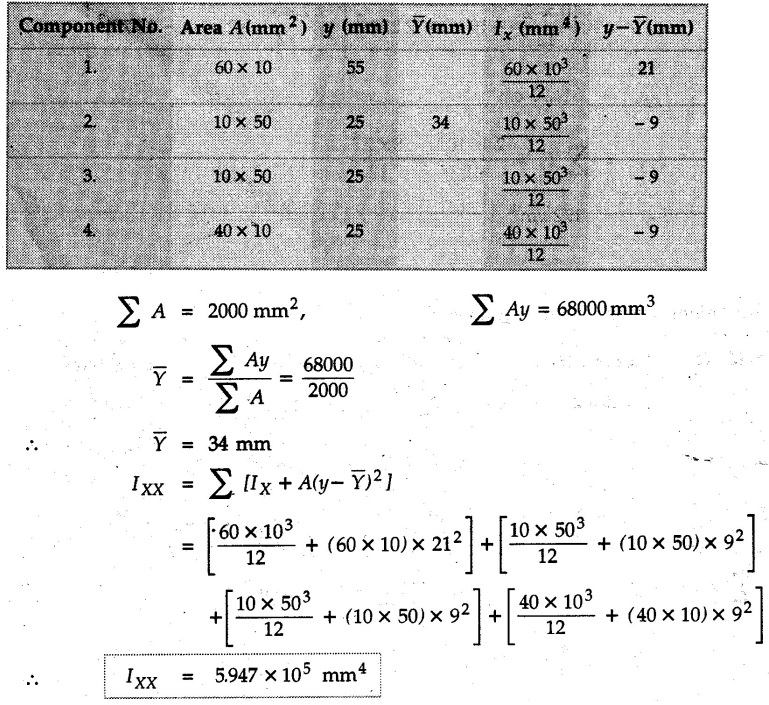
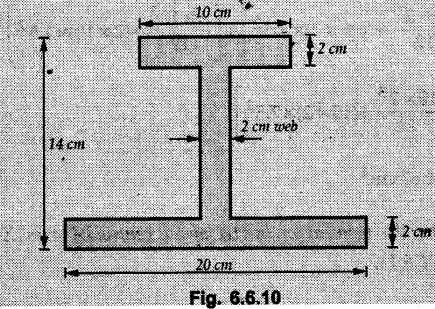
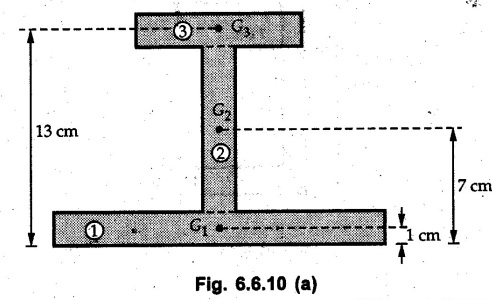
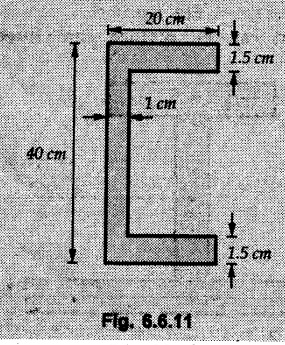
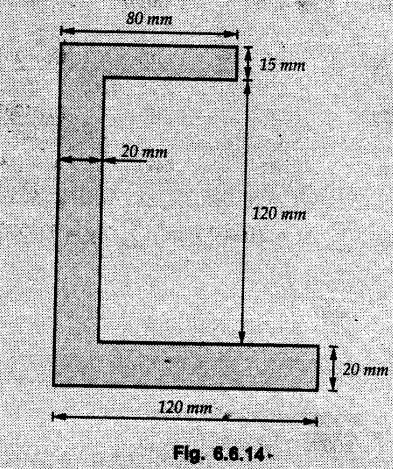
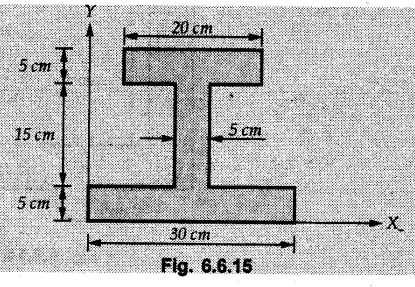
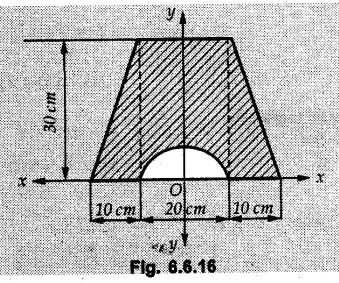
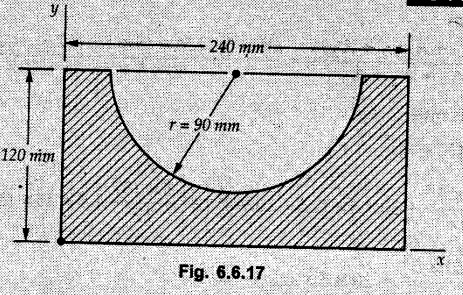
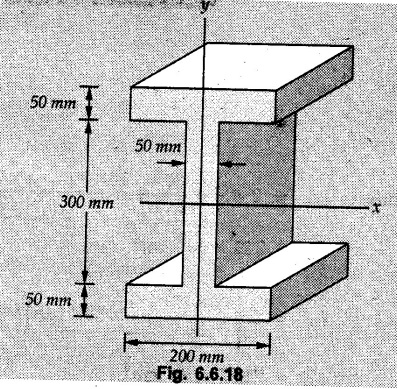
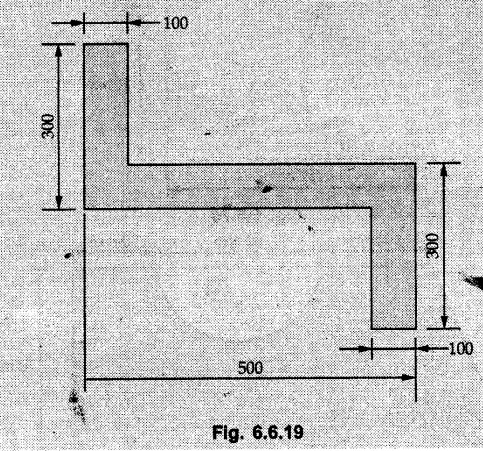
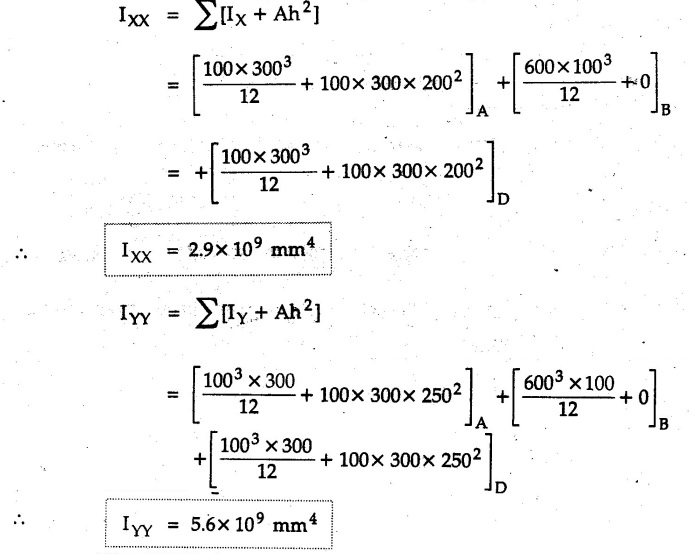
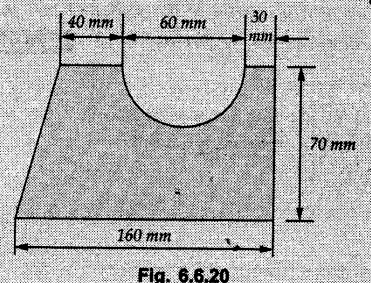
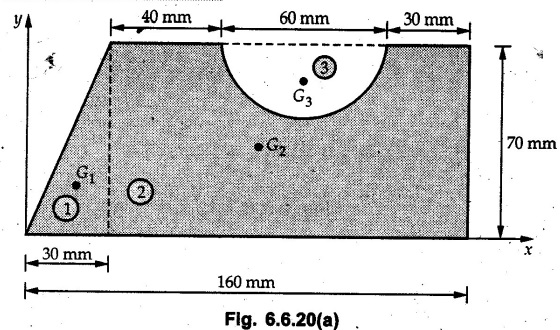
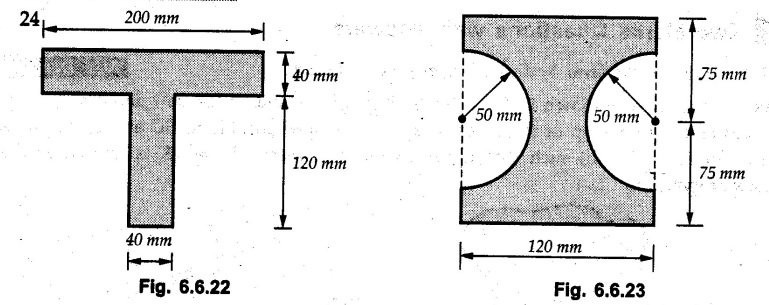
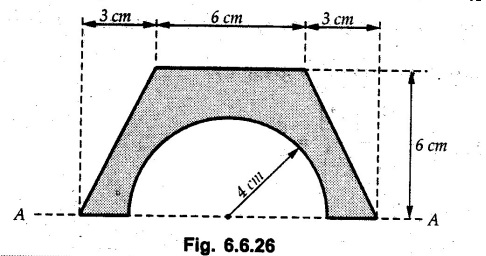
Example 6.6.1 Calculate the centroidal moment of inertia of the shaded area shown in Fig. 6.6.1. Solution: The area is symmetric about a vertical line passing through the centre which is the vertical centroidal axis. To determine position of horizontal centroidal axis, take base of the given area as reference. Divide the area into a square and two triangles from which a semicircle is removed as shown in Fig. 6.6.1 (a). The calculations are tabulated as follows: If origin is taken as shown in Fig. 6.6.1 (a), The centroid of first triangle is at a distance of 25 mm to the left and centroid of the second triangle is at distance of 25 mm to the right of origin. Example 6.6.2 Find the moment of inertia of the shaded area shown in Fig. 6.6.2 about the vertical and horizontal centroidal axes. The width of the hole is 200 min. Solution: The given area is symmetric about a vertical line passing through the centre. That line is the vertical centroidal axis. To find position of horizontal centroidal axis, find Example 6.6.3 Calculate the centroidal polar moment of inertia of a rectangular section with breadth of 100 mm and height of 200 mm. Solution: By perpendicular axes theorem, Example 6.6.4 For the plane section shown in Fig. 6.6.3, determine the area moment of inertia about its horizontal and vertical centroidal axes. Solution: The given area is symmetric about a vertical line passing through the centre. This line is vertical centroidal axis. To locate the horizontal centroidal axis, find The calculations are tabulated as follows: Example 6.6.5 A symmetrical trapezoidal lamina of top edge 60 mm and bottom edge 90 mm and of height 100 mm has a central hole of diameter 30 mm. Find the moment of inertia of the trapezium about XX. Refer Fig. 6.6.4. Solution: • The given area can be divided into two triangles and a rectangle from which a circle is removed. • The two triangles have base 15 mm and height 100 mm. The base of rectangle is 60 mm and height 100 mm. Moment of inertia of triangle and rectangle about their base are known. Use parallel axes theorem to find moment of inertia of circle about XX. Example 6.6.6 Find the moment of inertia of T-section shown in Fig. 6.6.5 about X-X passing through its centroid. All the dimensions are in mm. Solution: To find The calculations are tabulated as follows: Example 6.6.7 Determine the moments of inertia about centroidal axes and compute (1) Polar moment of inertia (ii) Radii of gyration of plane area shown in Fig. 6.6.6. Solution: Take origin as shown in Fig. 6.6.6 (a) and divide the given section into three rectangles. The calculations are tabulated as follows Example 6.6.8 Find the montent of inertia of the T-section shown in Fig. 6.6.7, about centroidal axis. Solution: A vertical line passing through the centre is the line of symmetry. Hence that line is the centroidal Y-axis. To find position of centroidal X-axis, find The calculations are tabulated as follows: Example 6.6.9 Fig. 6.6.8 shows a T-section of dimensions 10 × 10 × 2 cm. Determine the moment of inertia of the section about the horizontal and vertical axes, passing through the centre of gravity of the section. Solution: A vertical line passing through the centre is the line of sysmmetry. Hence that line is the centroidal Y-axis. To find position of centroidal X-axis, find Example 6.6.10 Determine the moment of inertia of the section shown in Fig. 6.6.9 about an axis passing through its centroid and parallel to the base. All dimensions are in mm. Solution: The given cross section can be divided into four rectangles as shown in Fig. 6.6.9 (a). The calculations are tabulated as follows: Example 6.6.11 Find the M.I. of the section shown in Fig. 6.6.10 about the centroidal axis X-X perpendicular to the web. Solution: The given section can be divided into three rectangles as shown in Fig. 6.6.10 (a). The calculations are tabulated as follows: Exampie 6.6.12 Determine the moment of inertia about centroidal axes X-X of the channel section shown in Fig. 6.6.11. Solution: The given area can be divided into three rectangles as shown in Fig. 6.6.11 (a). Taking the base of the figure as origin, the calculations are tabulated as follows : Example 6.6.13 Find the moment of inertia of a rolled steel joist girder of symmetrical I section shown in Fig. 6.6.12. Solution: The given cross section is symmetric about horizontal and vertical lines passing through the centre as shown in Fig. 6.6.12 (a). Divide the area into three rectangles as shown. All the three centroids coincide with Y-Y axis. The distances of centroids of component areas from X-X axis are shown in figure. The M.I. of rectangles (1) and (3) will be same about the two axes. Example 6.6.14 Find the moment of inertia of the section shown in Fig. 6.6.13 about centroidal X-X axis parallel to flange. The section is symmetrical about vertical centroidal axis. All dimensions are in mm. Solution: Take base of the given figure as reference to find The calculations are tabulated as follows: Example 6.6.15 Determine the location of the centroid and moment of inertia of the given lamina in Fig. 6.6.14 about centroidal X-axis. Solution: Choose origin and divide the given lamina into three rectangles as shown in Fig. 6.6.14 (a). The calculations are tabulated as follows: Example 6.6.16 Determine the moment of inertia of the given 'I' section given in the Fig. 6.6.15 about its horizontal and vertical axis passing through the centre of gravity. Solution: As the given area is symmetric about a vertical axis passing through its centre, As centroidal Y-axis coinsides with the vertical axis about which we are finding moment of inertia, Example 6.6.17 Find the moment of inertia of shaded area shown in Fig. 6.6.16 about Ix-x, axis and Iy-y axis. Solution: Example 6.6.18 Determine the moment of inertia of the shaded area as shown in Fig. 6.6.17 with respect to the x axis. Solution: For rectangle, Example 6.6.19 Determine the moment of inertia of the cross-sectional area (I section) of the channel with respect to the y axis Fig. 6.6.18. Solution: The centroidal y-axis of section coincides with centroidal y-axis of each rectangle. Example 6.6.20 Find the moment of inertia of the section shown in Fig. 6.6.19 about the x and y centroidal axes. All dimensionless in min. Solution: Example 6.6.21 Find the moments of inertia about the centroidal axes for the section shown in Fig. 6.6.20. Solution : The calculations are tabulated as follows : Example 6.6.22 Find the moment of inertia of a hollow rectangular plane shown Fig. 6.6.21about x-axis and y-axis through the centroid. Solution : Given Fig. 6.6.21(a) is symmetric about y-axis, Examples for Practice Q.1 Determine moment of inertia and radius of gyration of the 'T' section shown in Fig. 6.6.22 about centroidal Y-axis. (Ans. : IYY = 27.307 × 106 mm4, KYY = 46.19 mm) Q.2 Determine the moment of inertia of the section shown in Fig. 6.6.23 about centroidal axes X-X and Y-Y. (Ans. : Ixx = 28.84 × 106 mm4, lYY = 8.414 × 106 mm4) Q.3 For the plane area shown in Fig. 6.6.24 determine the area moment of inertia and radius of gyration about the X-axis. (Ans. : Ixx = 157.77 × 106 mm4, KYY = 80.75 mm) Q.4 Calculate the moment of inertia and radius of gyration about the X axis for the area shown in Fig. 6.6.25. (Ans. : Ixx = 4.046 × 106 mm4, Kxx = 34.03 mm) Q.5 The cross section of a culvert is shown in Fig. 6.6.25. Compute the moment of inertia about the A-A axis. Fig. 6.6.26 (Ans. : IAA = 439.45 cm4)Solved Examples for Understanding


![]() = 0.
= 0.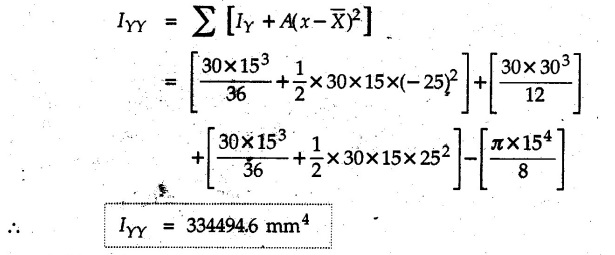
![]() by taking base of the given figure as reference.
by taking base of the given figure as reference.

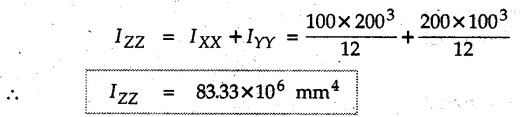
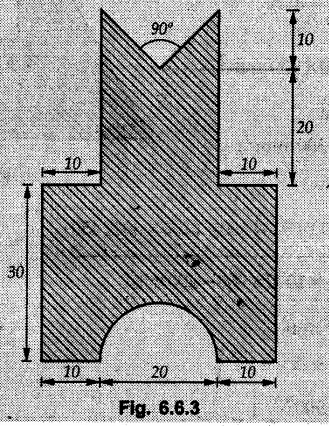
![]() . Take base of the given section as reference. The shaded area can be obtained by adding areas of the two rectangles and subtracting the triangle and semicircle as shown in Fig. 6.6.3 (a).
. Take base of the given section as reference. The shaded area can be obtained by adding areas of the two rectangles and subtracting the triangle and semicircle as shown in Fig. 6.6.3 (a). 

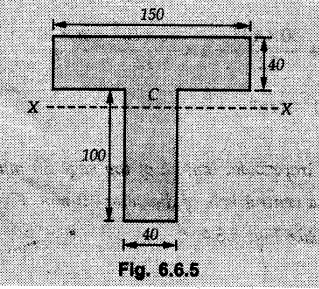
![]() take base of the given section as reference and divide it into two rectangles as shown in Fig. 6.6.5 (a).
take base of the given section as reference and divide it into two rectangles as shown in Fig. 6.6.5 (a).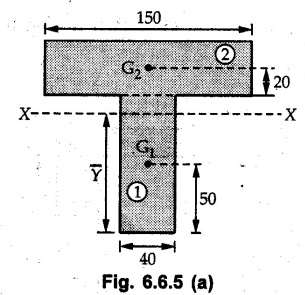

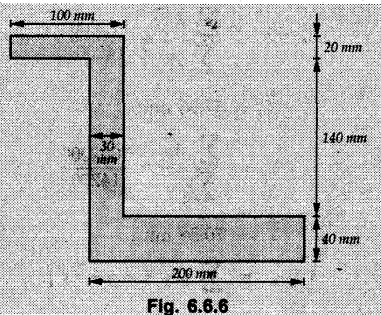


![]() by taking base of the section as reference.
by taking base of the section as reference. 

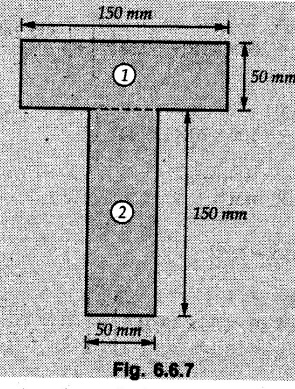
![]() by taking base of the section as reference. The calculations are tabulated as follows:
by taking base of the section as reference. The calculations are tabulated as follows:






![]() Divide the figure into three rectangles as shown in Fig. 6.6.13 (a).
Divide the figure into three rectangles as shown in Fig. 6.6.13 (a).


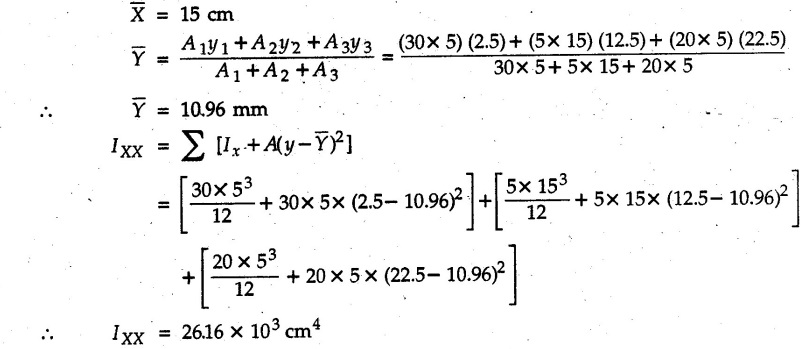
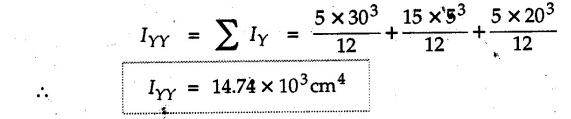
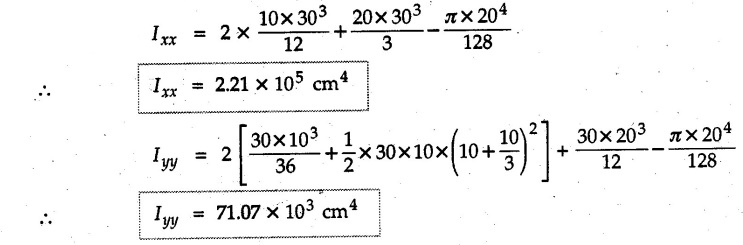

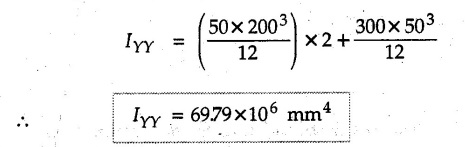




Engineering Mechanics: Unit III: Distributed Forces : Tag: : - Solved Example & Practice Problems: Moment of Inertia of Composite Areas
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
