Engineering Mechanics: Unit III: Distributed Forces
Solved Example & Practice Problems: Mass Moment of Inertia
Solved Example Problems, Examples for Practice: Mass Moment of Inertia: Parallel Axis Theorem, Distributed Forces - Engineering Mechanics
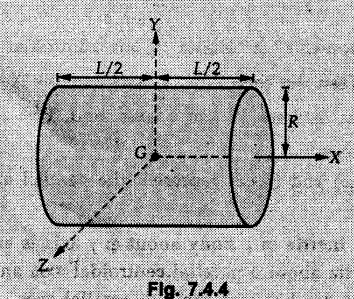
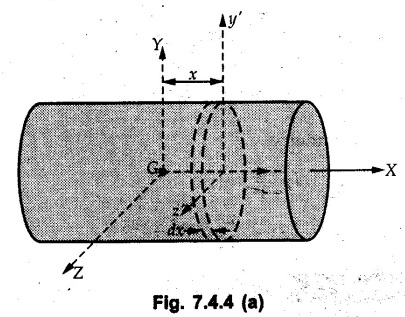
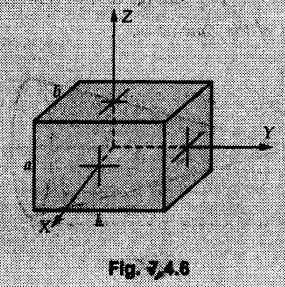
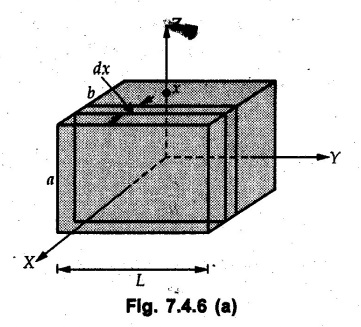
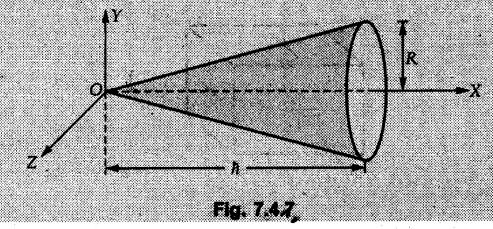
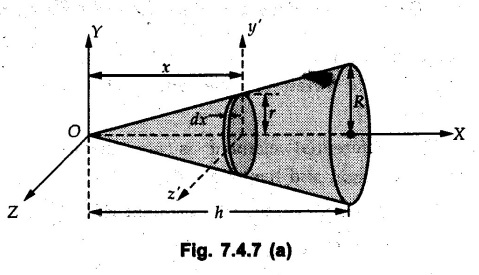
Solved Examples for Understanding Example 7.4.1 Determine the mass moment of inertia of a rod of length L and a small area of cross section A about an axis perpendicular to its length at its end. Solution: Consider a small element of length dx at distance x from one end as shown in Fig. 7.4.3. Volume of the element dV = A dx Mass of the element dm = ρ A dx Example 7.4.2 Determine mass moment of inertia of a cylinder shown in Fig. 7.4.4 about X, Y and Z axes. Solution: Consider the differential element to be a disc of radius R, thickness dx at distance x from G as shown in Fig. 7.4.4 (a). For the differential element, The moment of inertia of differential element about y' axis is By parallel axis theorem, Example 7.4.3 Determine moment of inertia of a solid sphere of radius R and mass m about its centroidal axis. Solution: Consider the differential element to be a disc of radius r and thickness dx at distance x from the origin as shown in Fig. 7.4.5. Example 7.4.4 A rectangular prism is shown in Fig. 7.4.6. The origin is at the geometric centre of the prism. The X, Y and Z-axes pass through the mid points of faces. Derive the mass moment of inertia of the prism about the X-axis. Solution: Choose a slab perpendicular to X-axis as the differential element as shown in Fig. 7.4.6 (a). The differential element is at distance x from the origin and has width dx. The volume of differential element is, dV = aL dx Mass of differential element is dm = ρ aL dx As the X-axis is perpendicular to the plane of the disc, Example 7.4.5 Determine the moment of inertia of the cone shown in Fig. 7.4.7 about the X, Y and Z axes. Take mass of the cone as m. Solution: Consider the differential element to be a disc at distance x from 0 and of width dx and radius r as shown in Fig. 7.4.7 (a). By similarity of triangles, Moment of inertia of disc about X-axis is, The moment of inertia of disc about y' axis is, ⸫ By parallel axes theorem, its moment of inertia about Y-axis is, By symmetry, Examples for Practice Q.1 Determine the mass moment of inertia of a rod of length L and a small area of cross section A about an axis passing through its centre and perpendicular to its length. Q.2 Determine moment of inertia of the rectangular prism shown in Fig. 7.4.8 about Y-axis.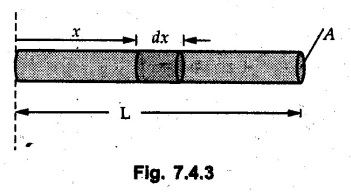


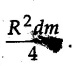

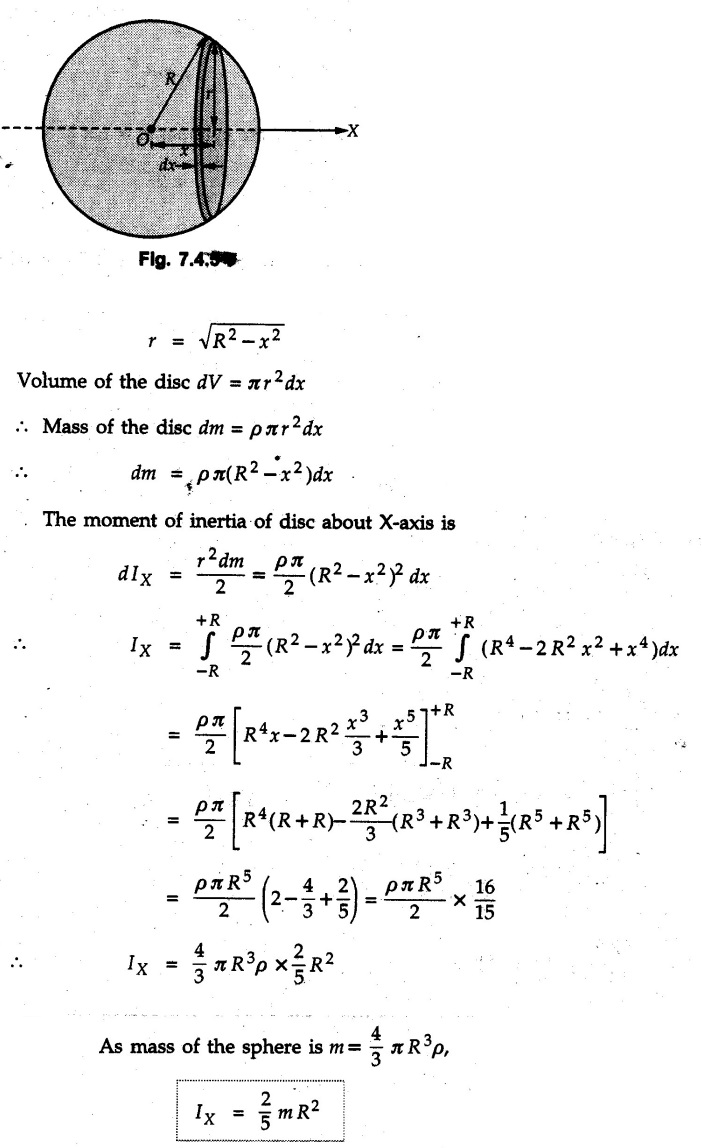

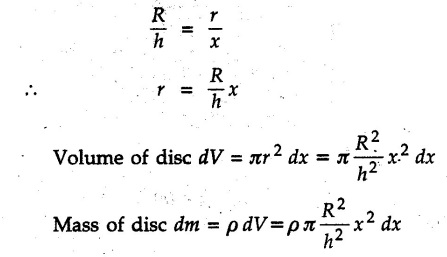
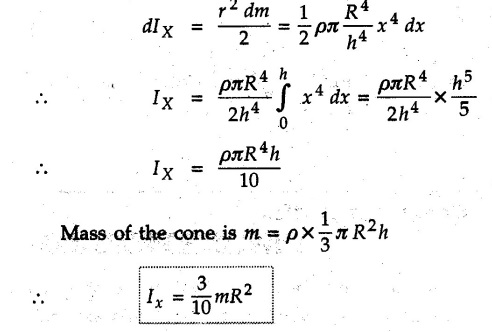
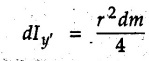

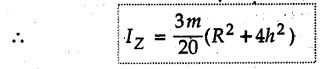


Engineering Mechanics: Unit III: Distributed Forces : Tag: : - Solved Example & Practice Problems: Mass Moment of Inertia
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
