Engineering Mechanics: Unit I: Statics of Particles
Solved Example & Practice Problems: Magnitude of resultant
Miscellaneous Solved Examples: Statics of Particles - Engineering Mechanics
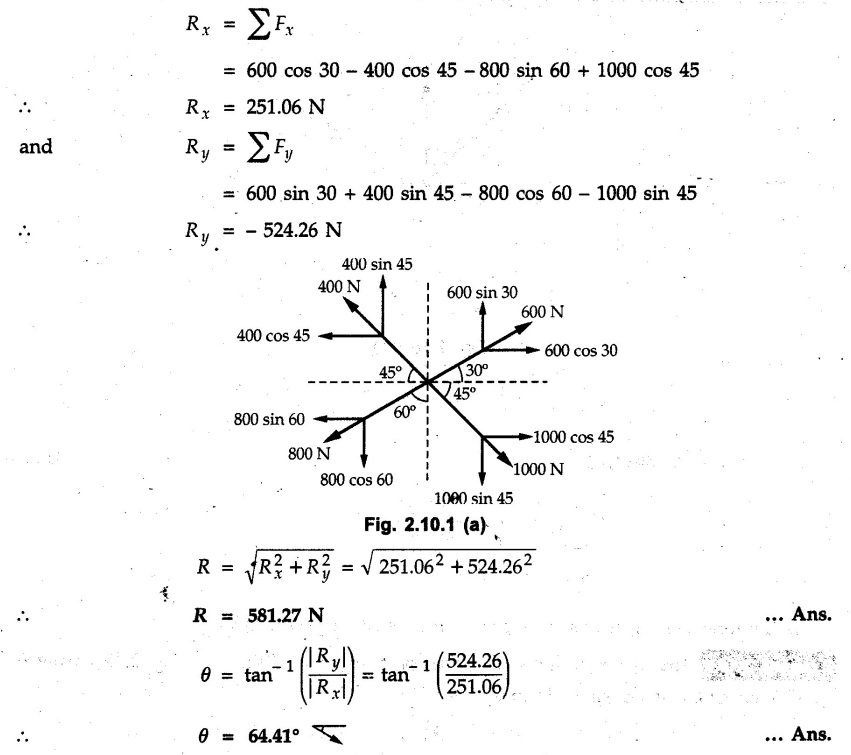
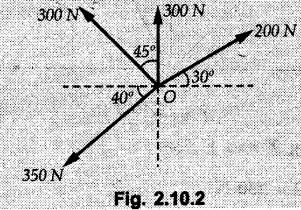
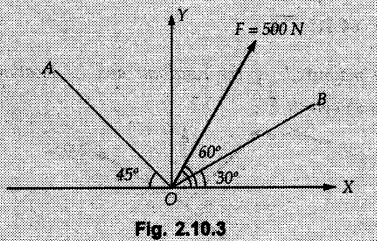
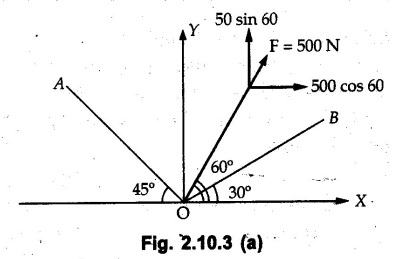
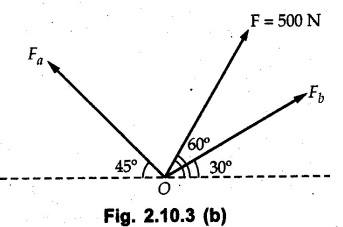
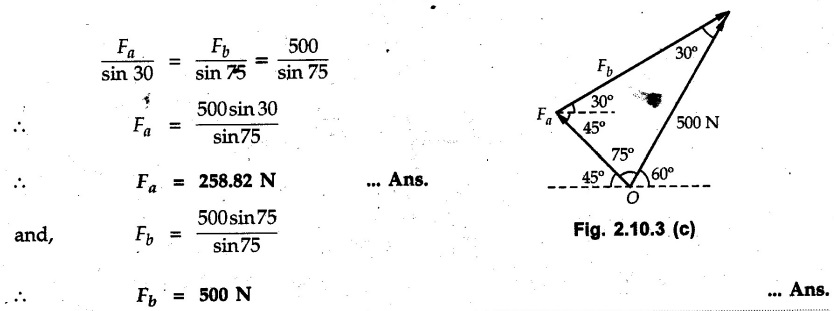
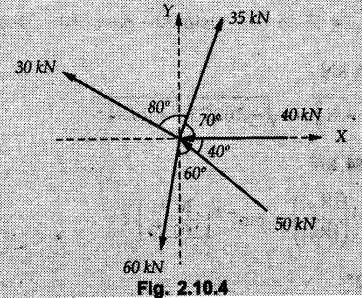
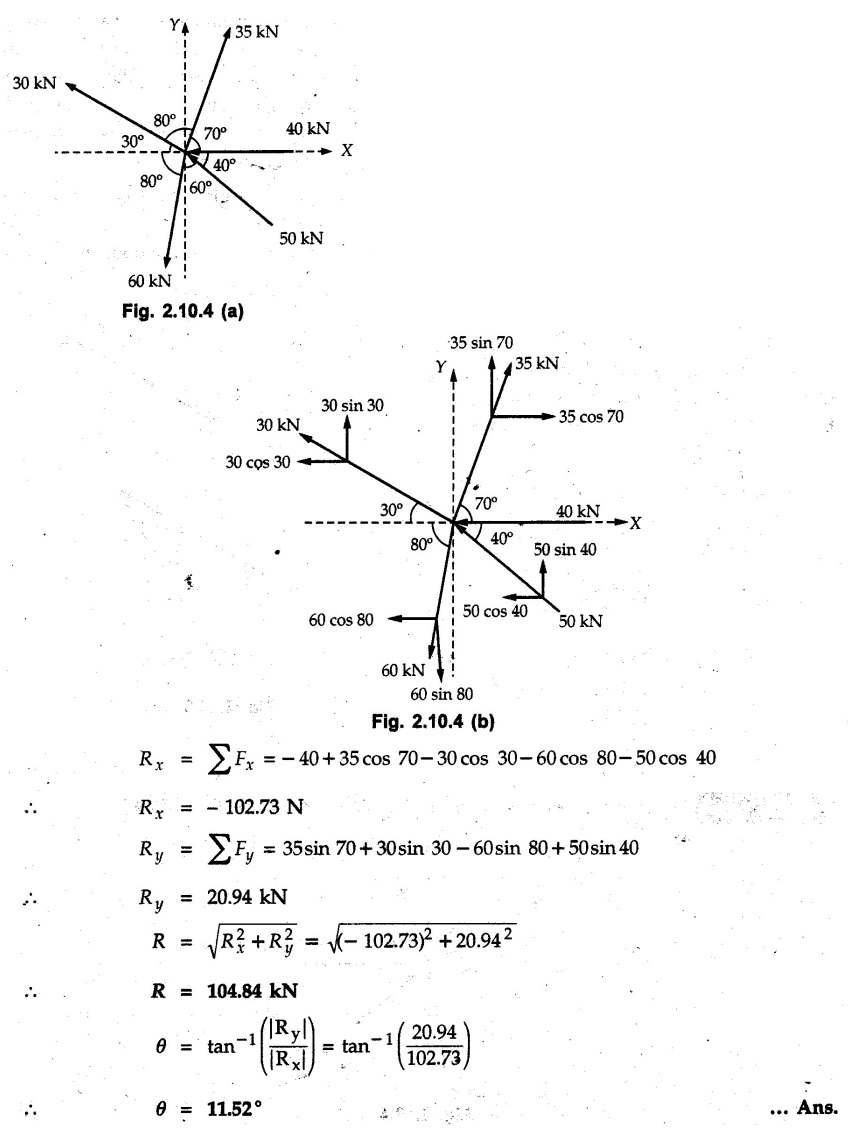
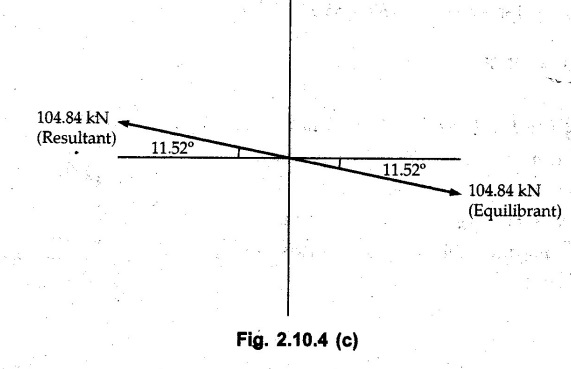
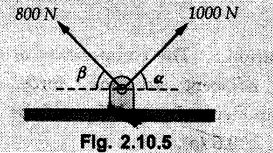
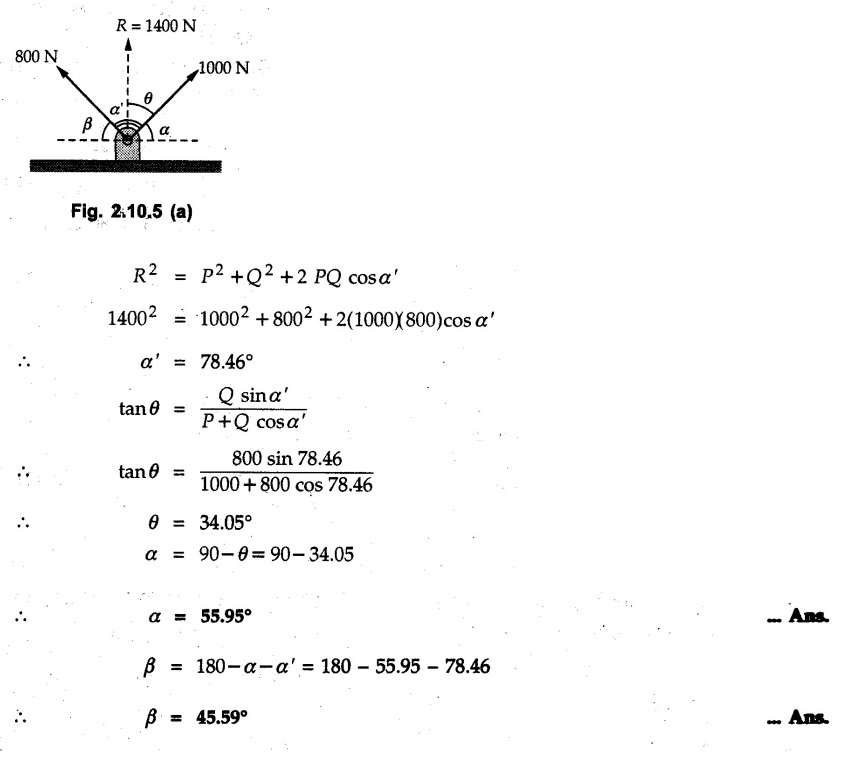
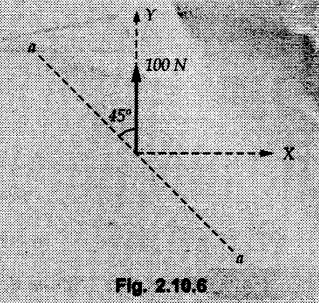
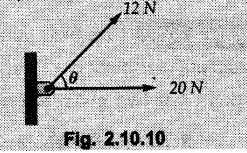
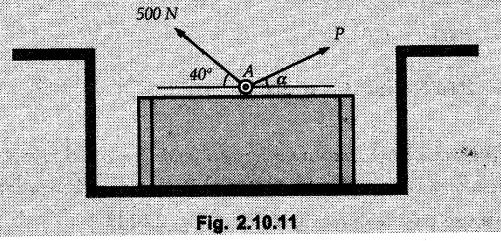
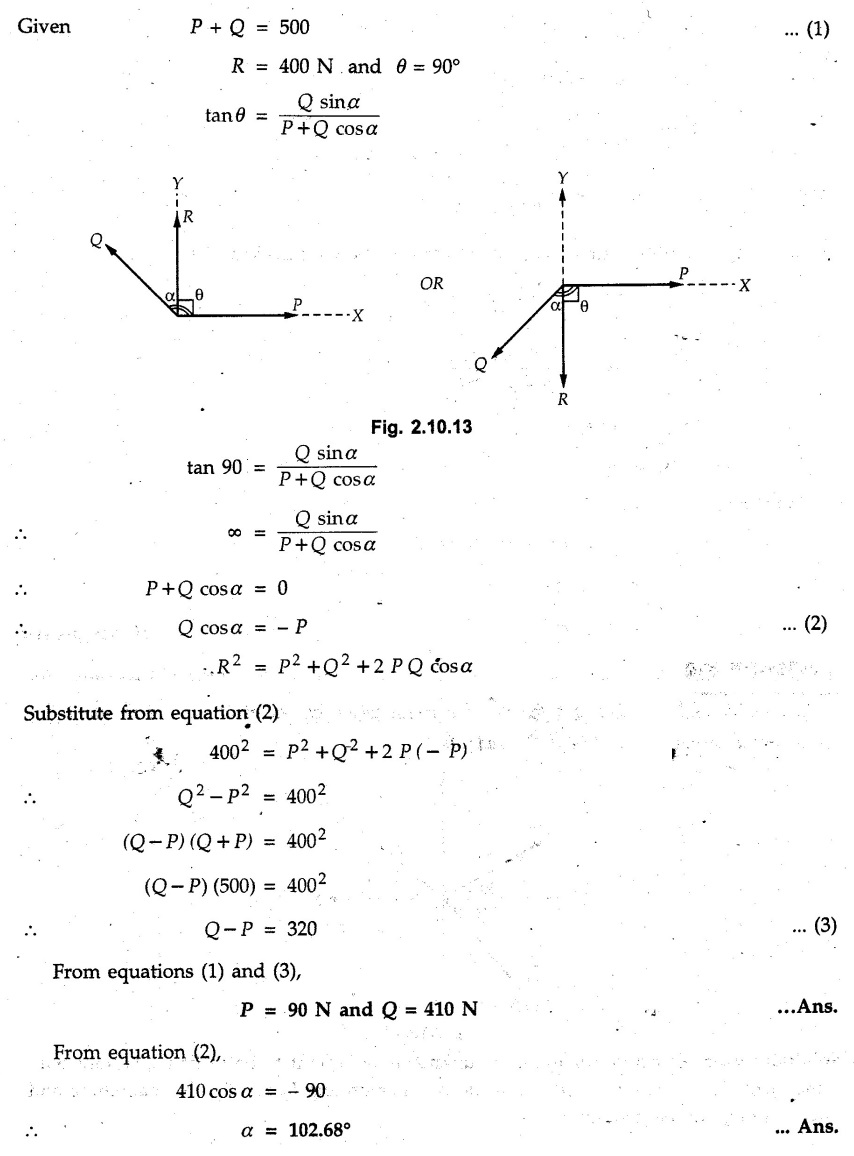
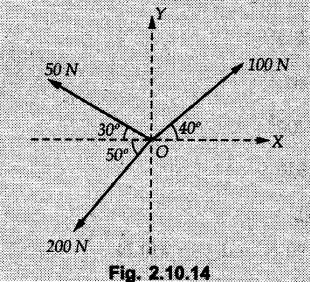
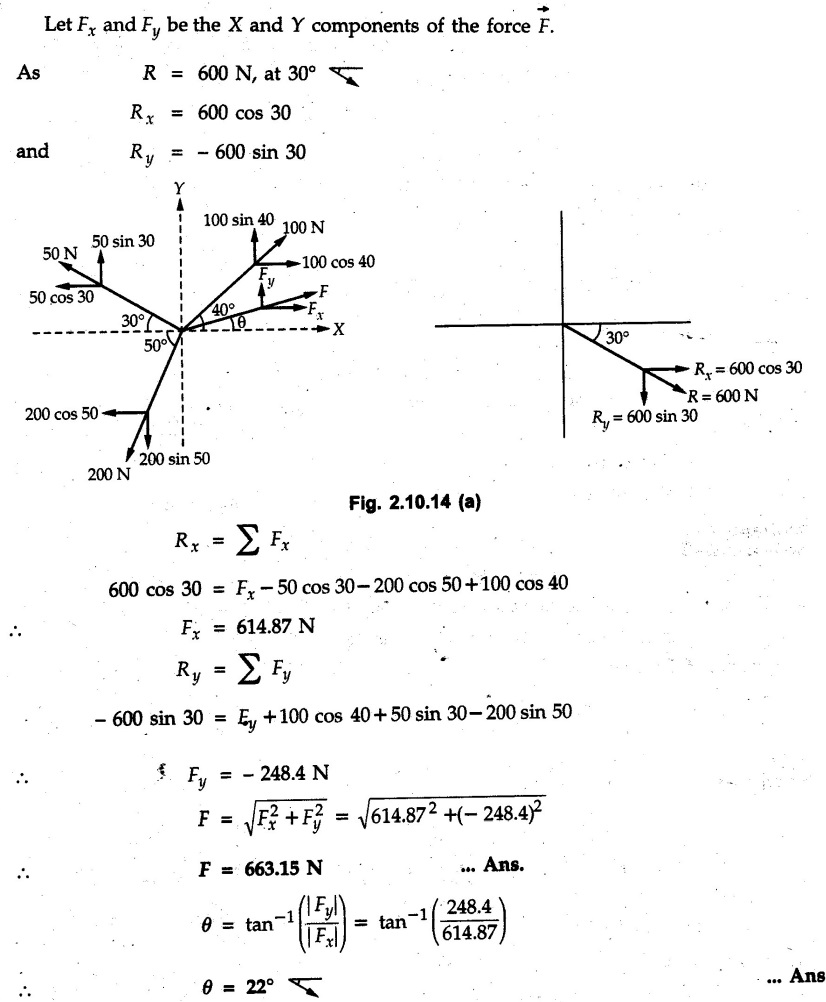
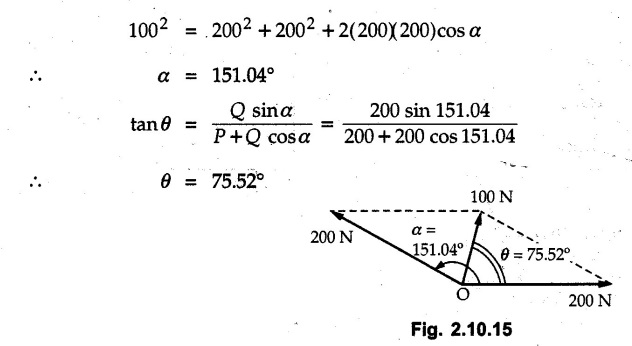
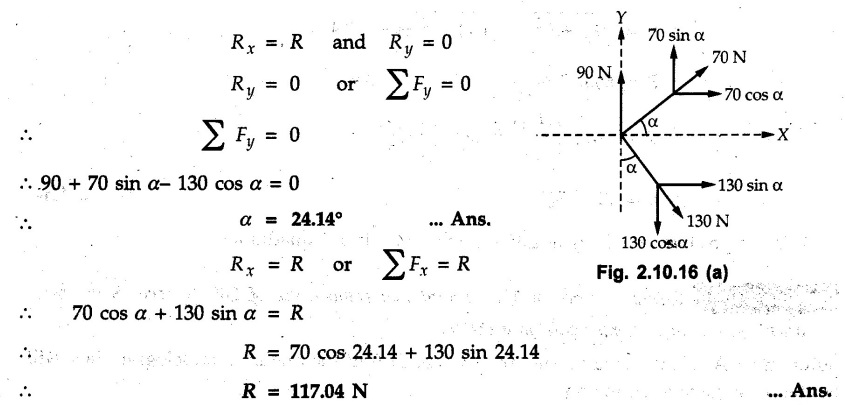
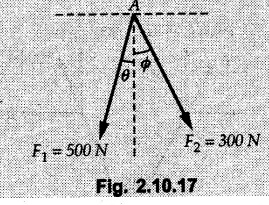
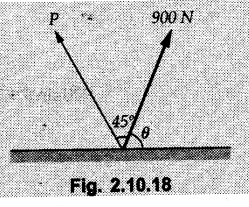
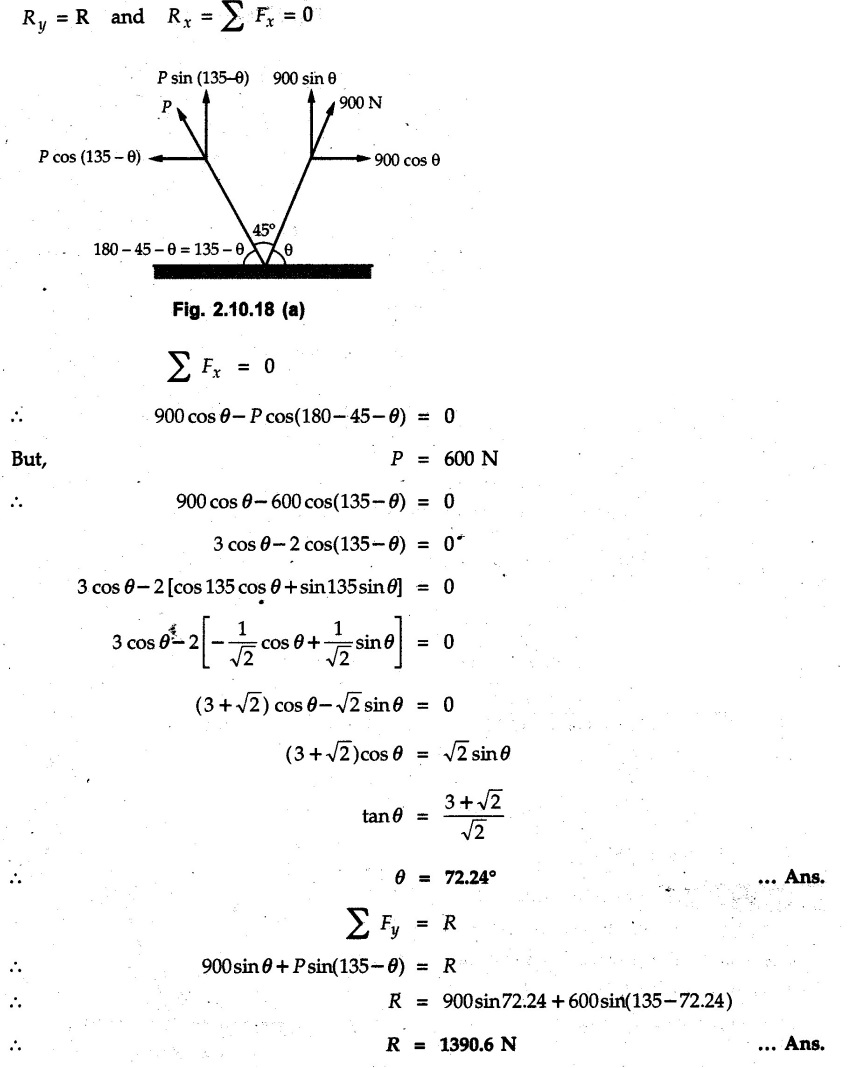
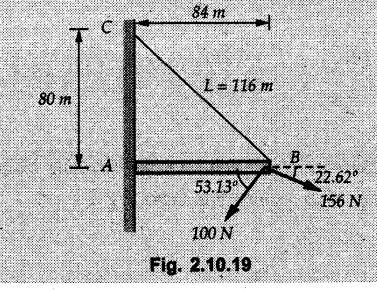
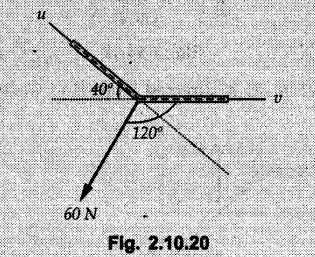
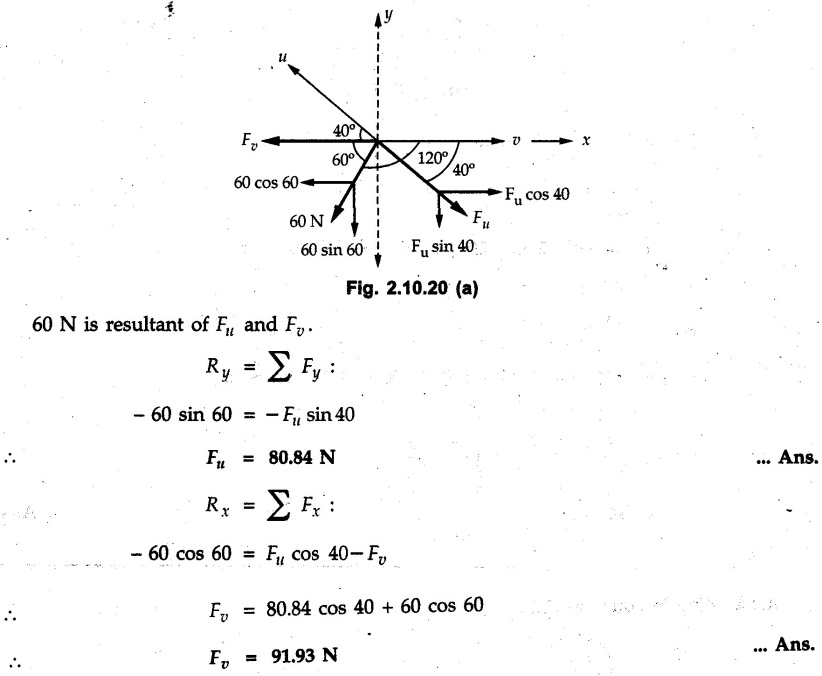
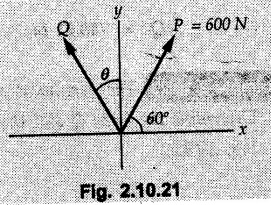
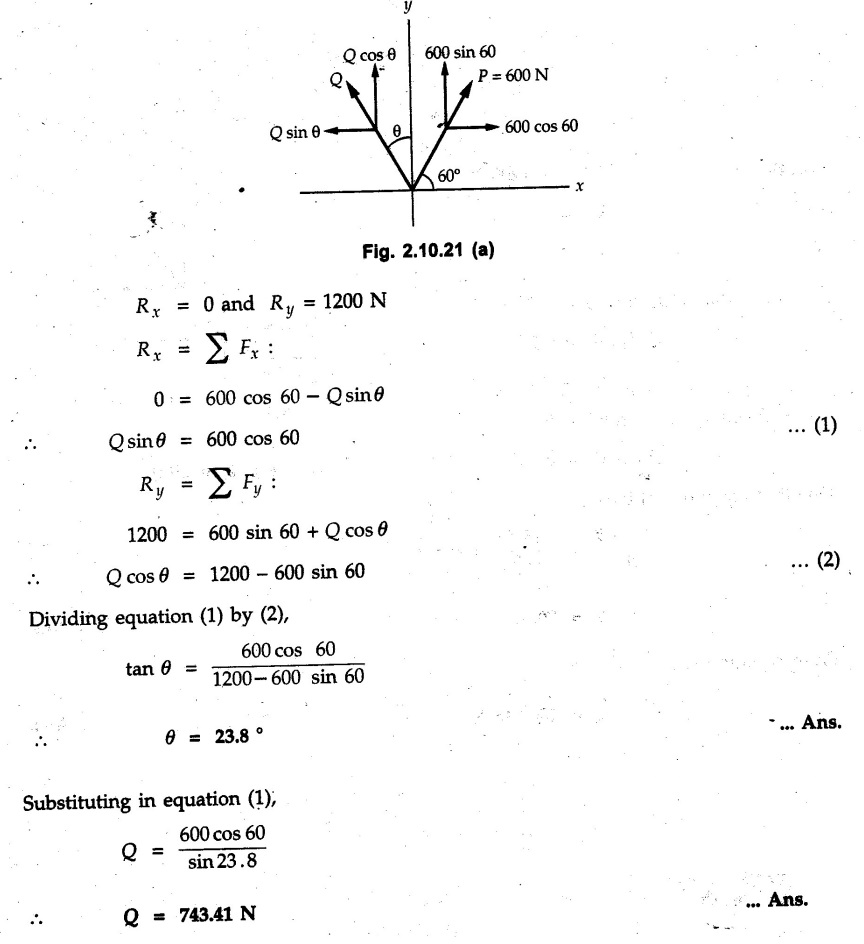
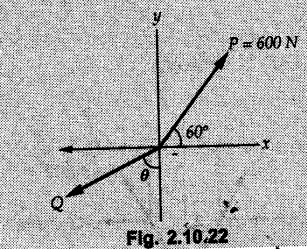
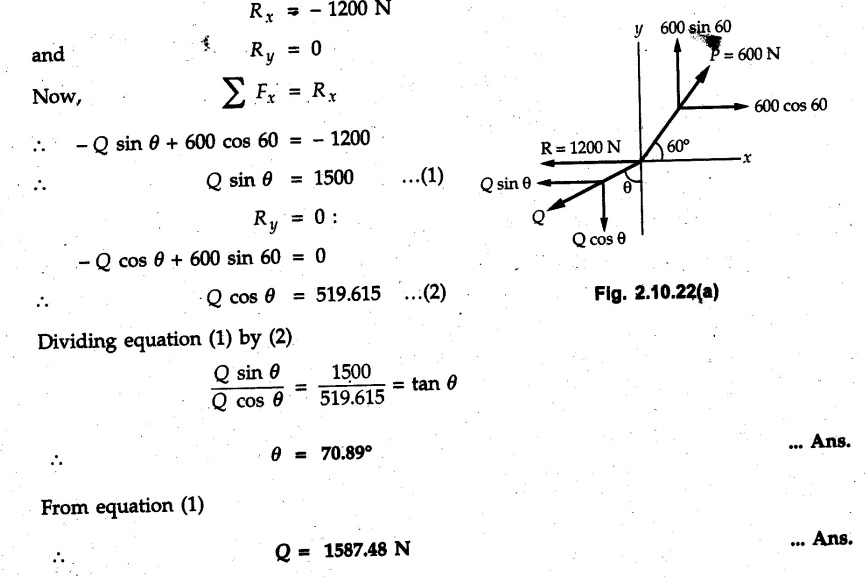
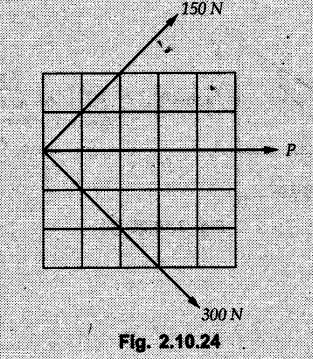
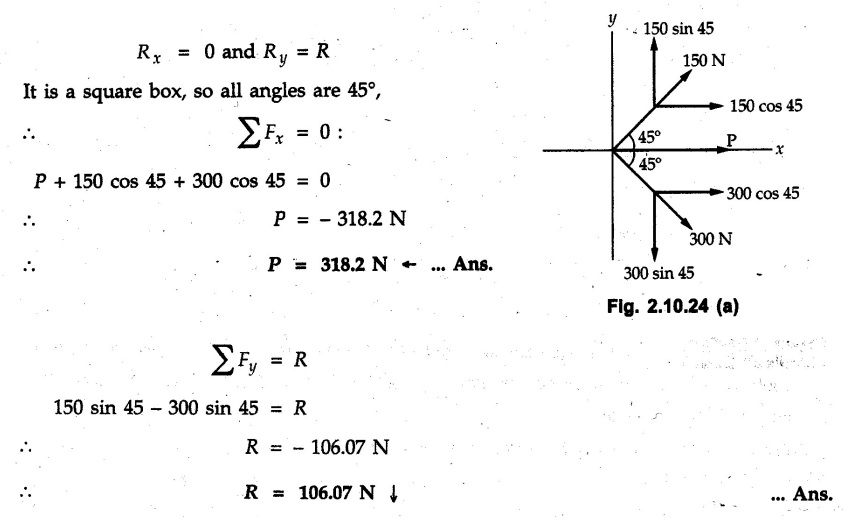
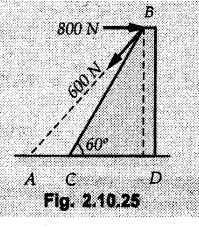
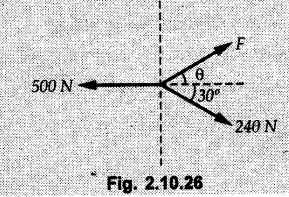
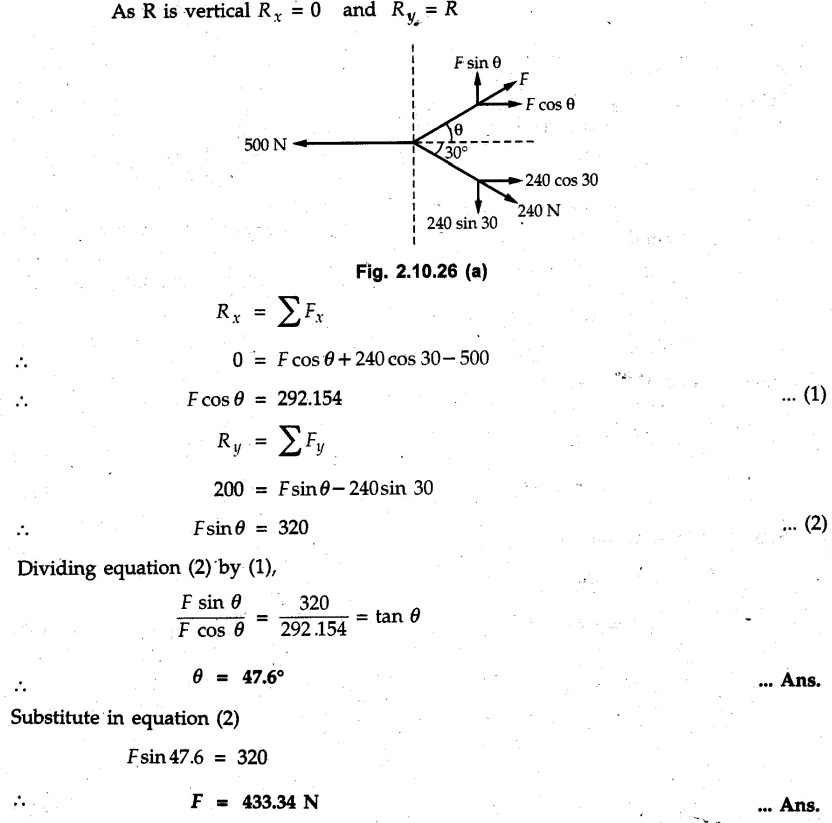
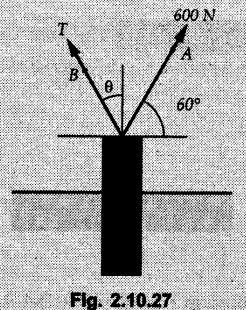
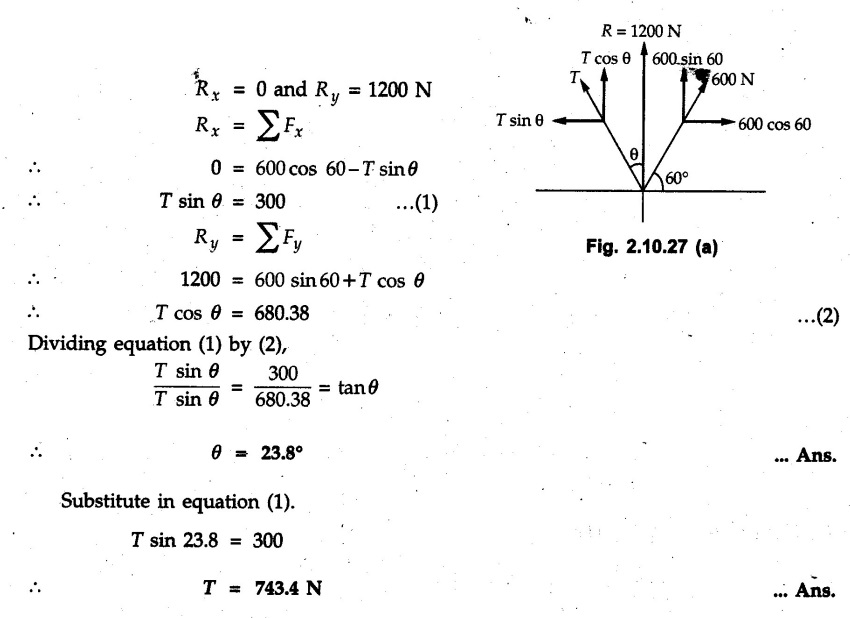
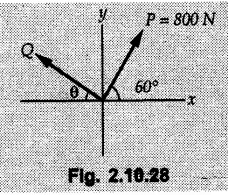
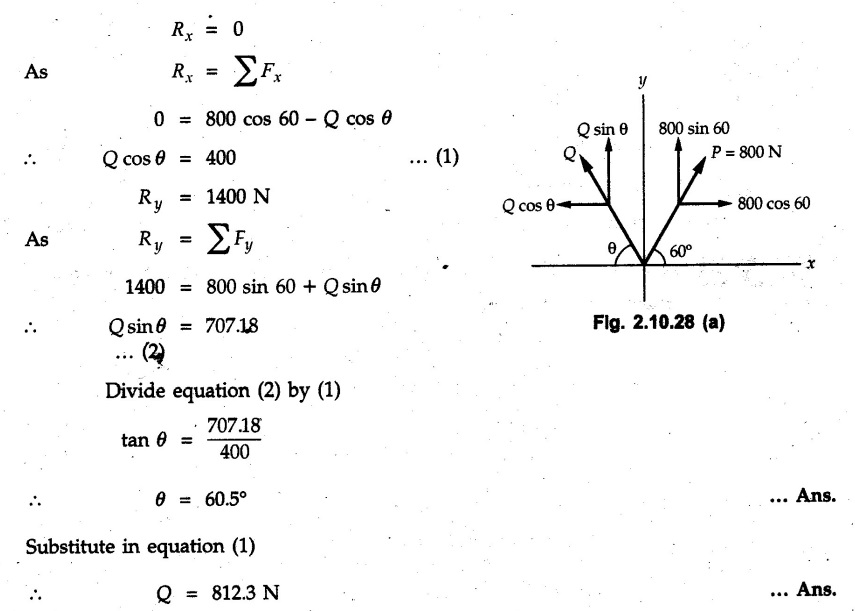
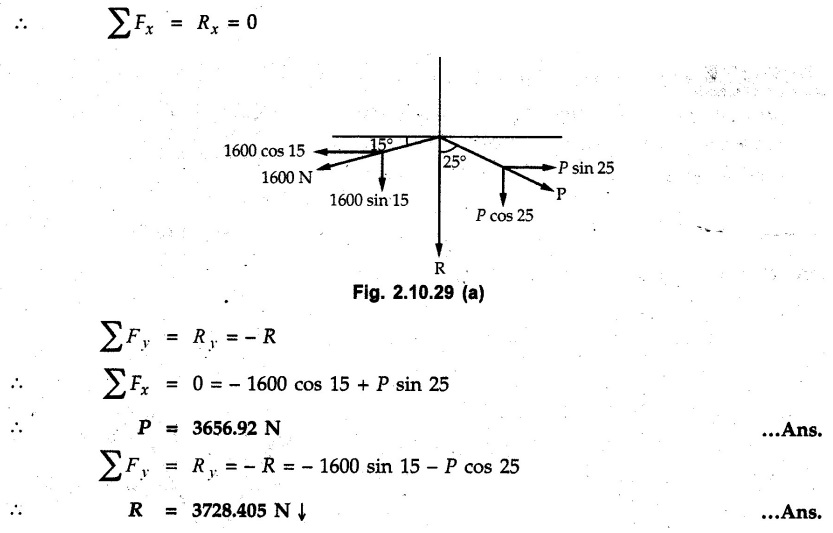
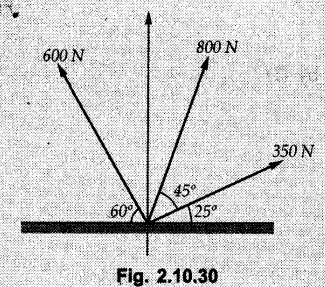
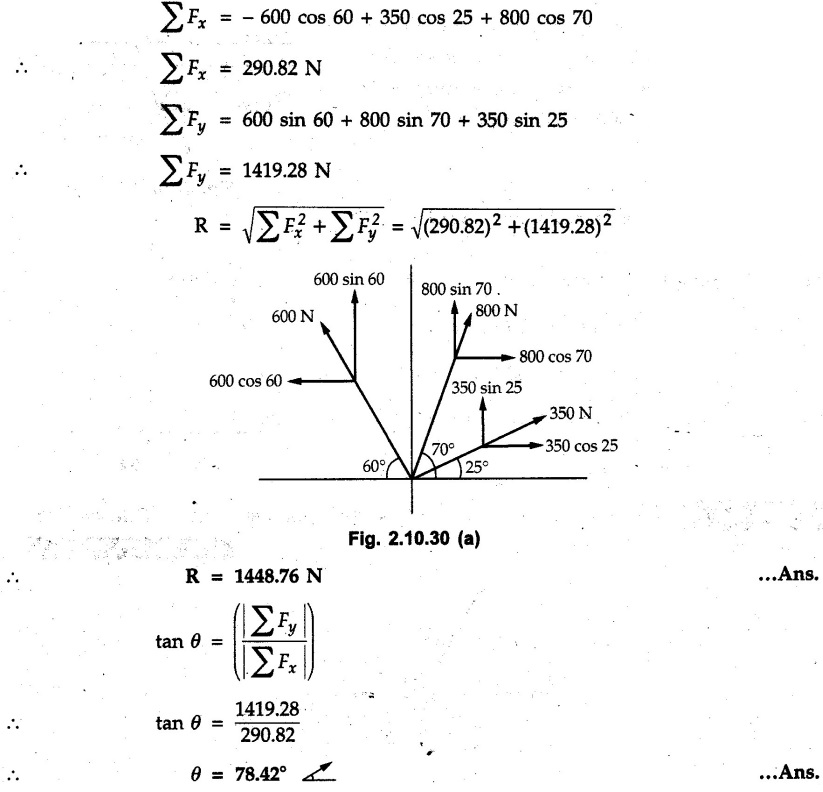
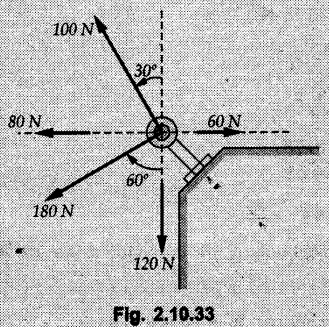
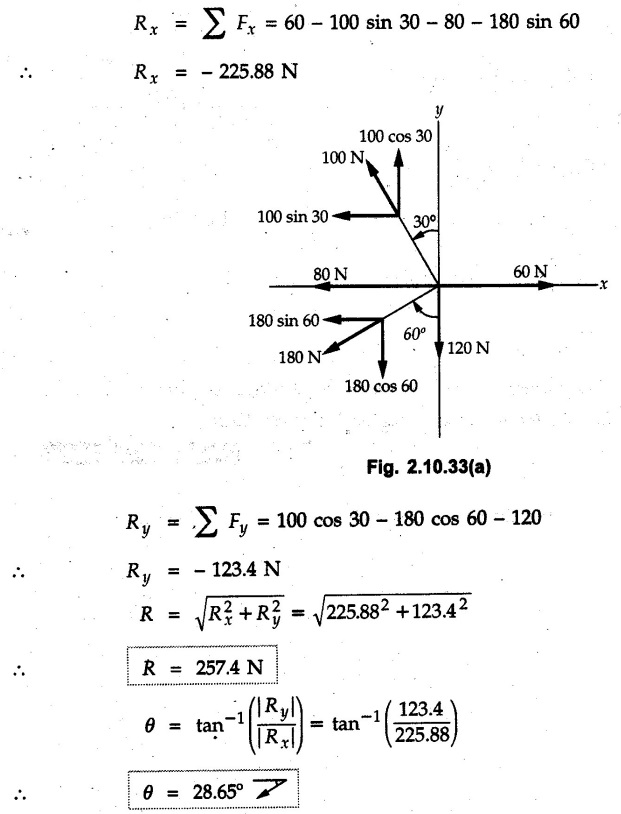
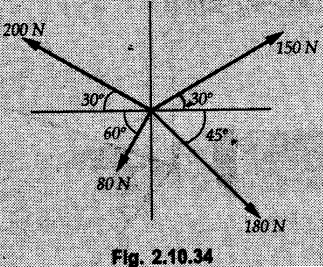
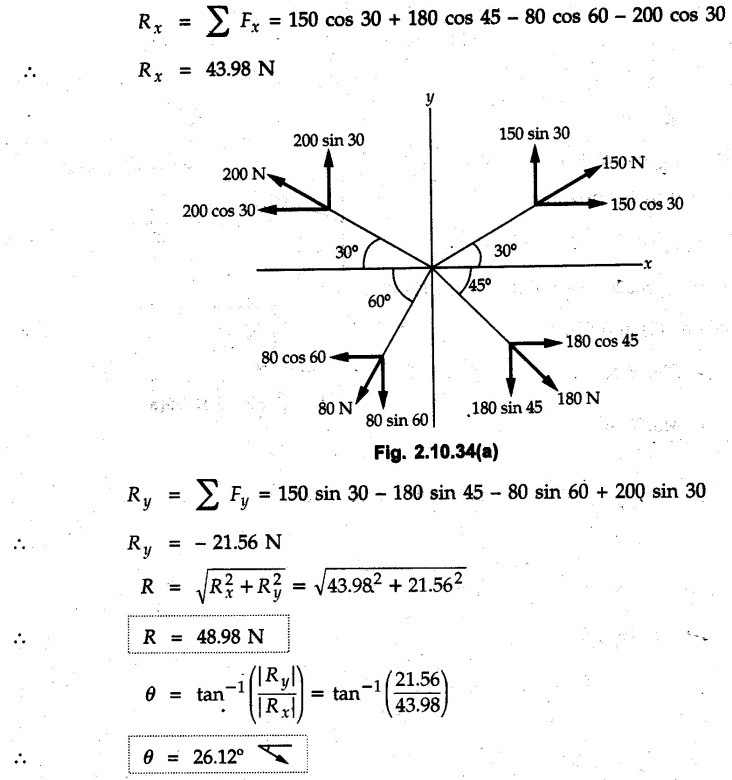
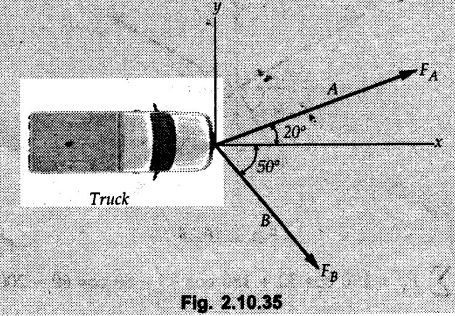
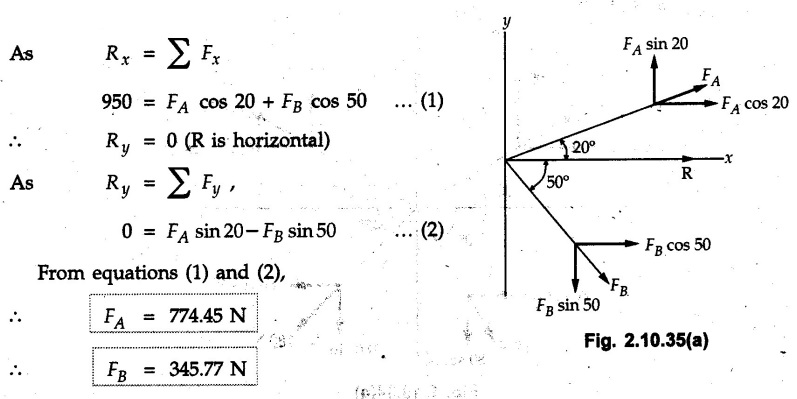
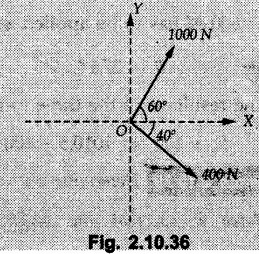
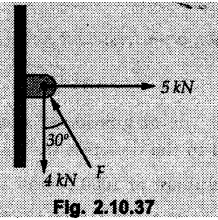
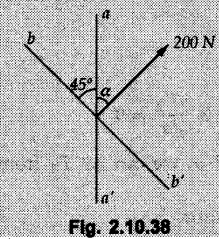
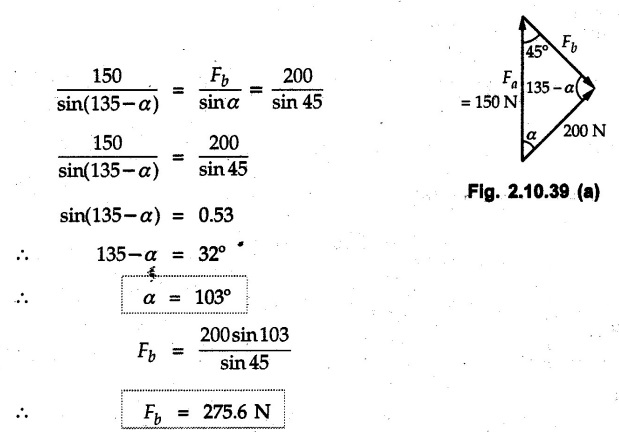
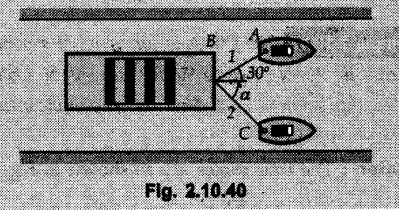
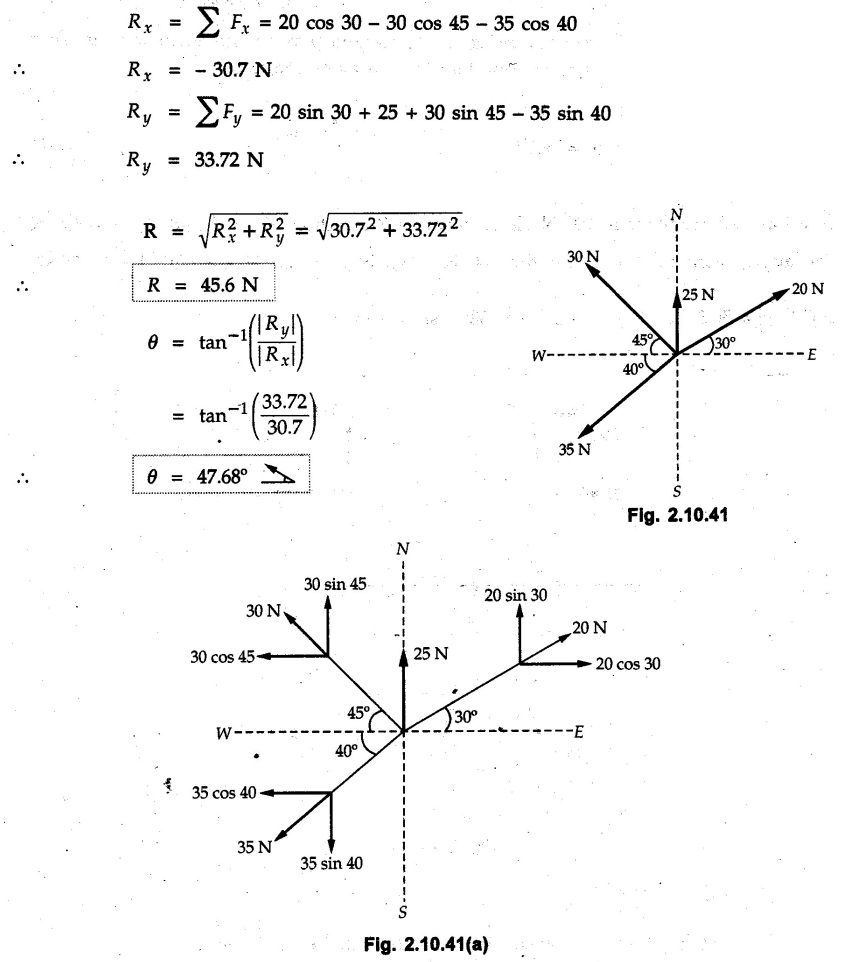
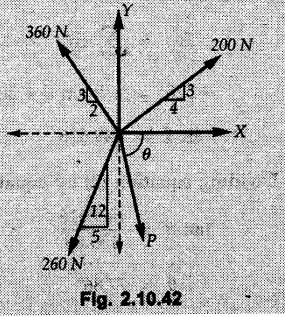
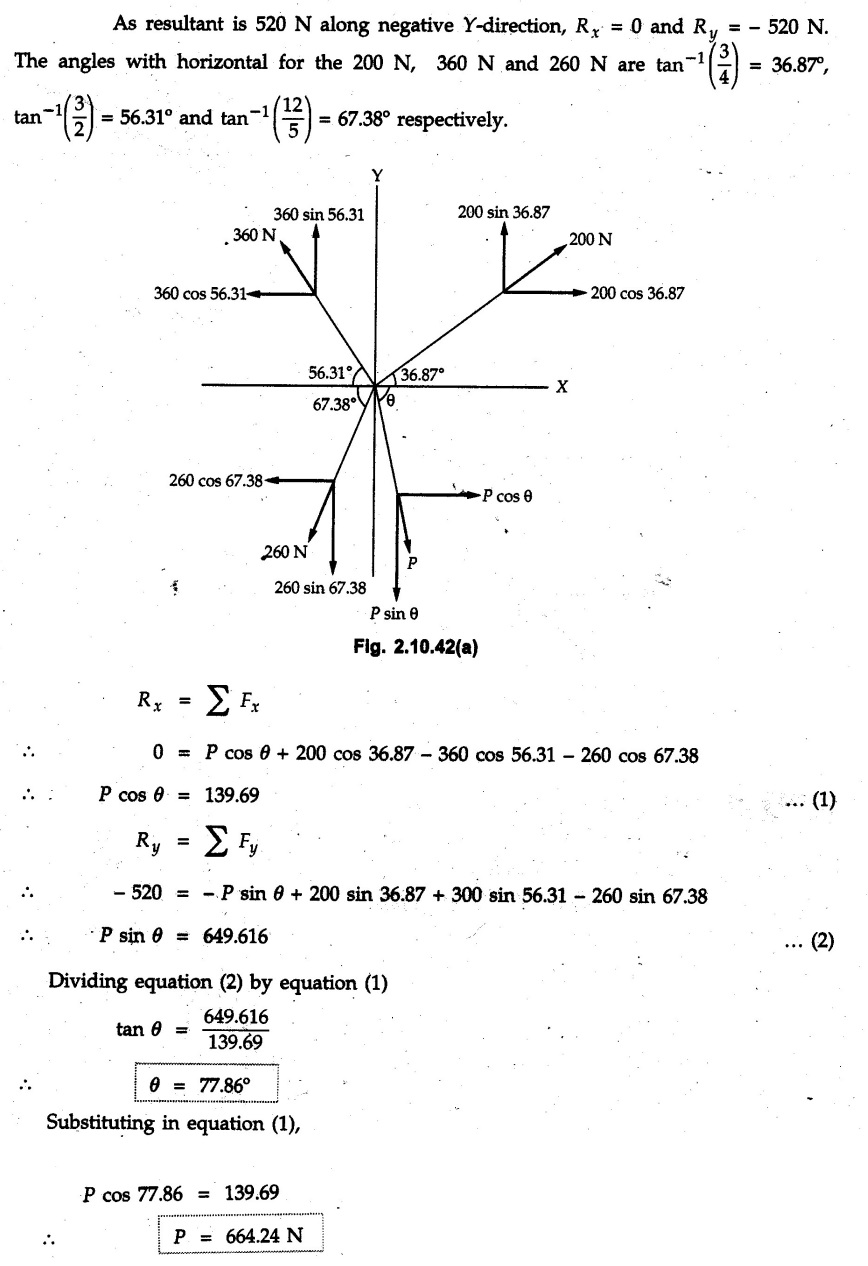
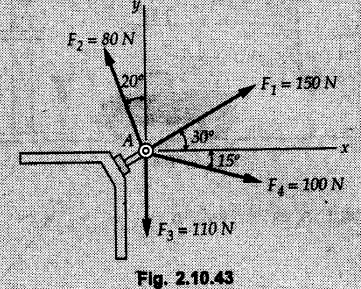
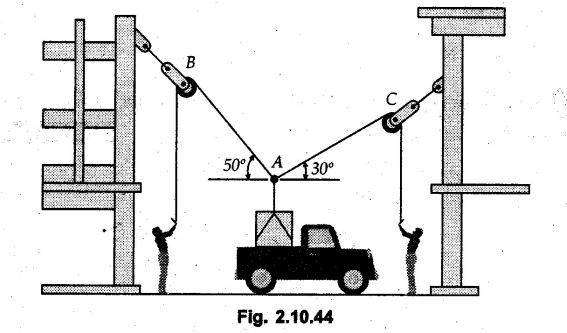
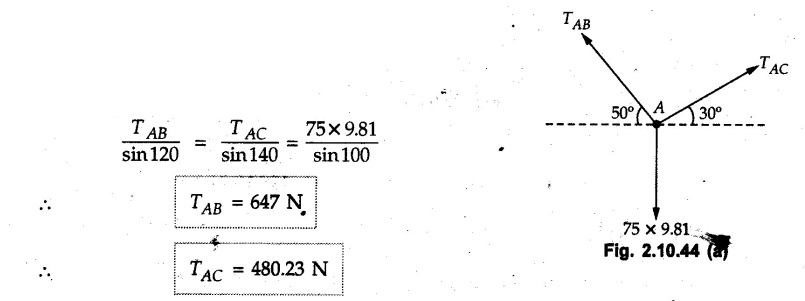
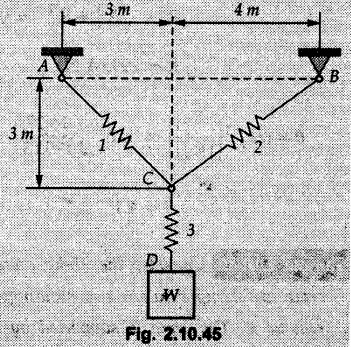
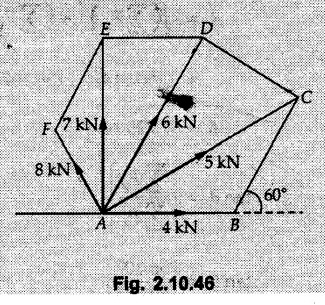
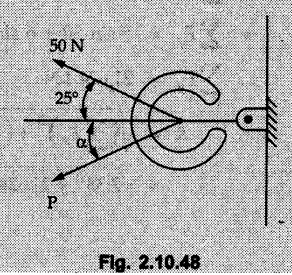
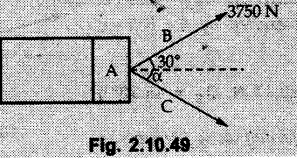
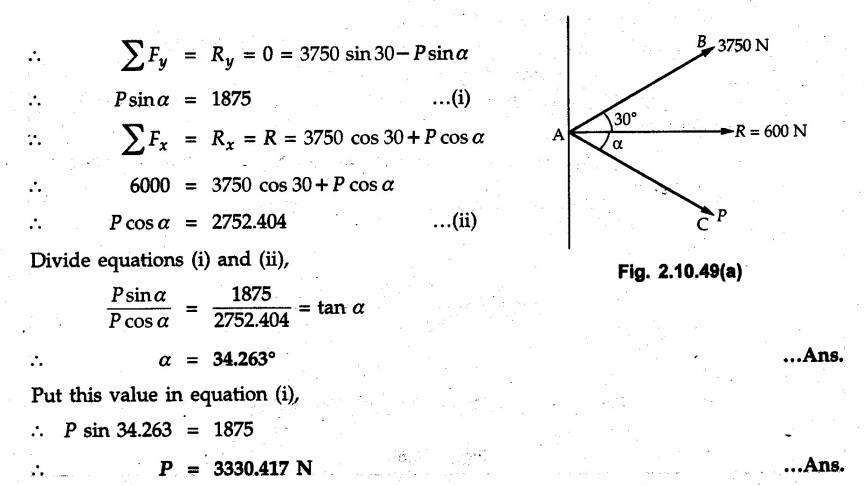
Miscellaneous Solved Examples Example 2.10.1 Determine the resultant force in magnitude and direction for concurrent force system as shown in Fig. 2.10.1. Solution : Example 2.10.2 Find the magnitude of the resultant and its location of the following forces acting at a point O as shown in Fig. 2.10.2. Solution: As the force system is concurrent at O, the resultant passes through O. Example 2.10.3 Find the magnitudes of resolved parts of force 'F' shown in Fig. 2.10.3 along OA and OB, and also along the axes X and Y. Solution: • Components along X and Y axes : • The angle between OA and OB is 180 - 45 - 30 = 105° • The components are along two non perpendicular directions for which we can use rectangular components, triangle law or Lami's theorem as magnitudes of the two components are unknown. • Here we give the solution by triangle law. Students are advised to solve by remaining two methods as well. • The 500 N force will be resultant of its components say, Fa and Fb along OA and OB. Refer Fig. 2.10.3 (b). The triangle is formed by drawing Fb from the tip of Fa and the resultant 500 N from the base of Fa to the tip of Fb as shown in Fig. 2.10.3 (c). Using sine rule, Example 2.10.4 Determine the equilibrant of the force system shown in Fig. 2.10.4. Solution: • To find equilibrant, we have to first calculate the magnitude and direction of resultant force. Equilibrant is then a force having same magnitude as resultant but opposite direction. • As the problem involves resultant of more than two forces, we have to use rectangular components. The angles of 30 kN and 60 kN with negative X-axis will be 30° and 80° respectively as shown in Fig. 2.10.4 (b). Equilibrant is a force of magnitude 104.84 kN acting at an angle of 11.52° in 4th quadrant as shown in Fig. 2.10.4 (c). Example 2.10.5 Forces are transmitted by two members as shown in Fig. 2.10.5. If the resultant of these forces is 1400 N directed vertically upward, find angles α and ß. Solution: As two angles are unknown, the parallelogram law will be convenient to use. • Let P 1000 N, Q = 800 N. Their resultant is R = 1400 N as shown in Fig. 2.10.5 (a). • The angle between P and Q is α' and angle made by R with P is θ as shown in Fig. 2.10.5 (a). Example 2.10.6 The 100 N vertical force is to be replaced by two forces, F1 directed along the 45° line α-a and F2 which has magnitude 80 N. Calculate the magnitude of F1 and the anticlockwise angle α made by F2 with x-axis. Refer Fig. 2.10.6. Solution: The components of force have to be adjacent to the force. Hence the components F1 and F2 will be as shown in Fig. 2.10.6 (a). • As resultant is vertical its x-compnent (Rx) is zero. The 100 N force will be resultant of F1 and F2. Note: Equation (3) can be solved on scientific calculators to obtain one value of α. i.e. α = 17.11. It should be remembered that trigonometric equations like equation (3), where coefficients of sina and cos a are equal, have two solutions for α. One solution is α and the other 90 - α. Example 2.10.7 Replace the 1000 N force shown in Fig. 2.10.7 by two forces, a 500 N force acting in the negative Y direction and a force Solution: The 1000 N force will be resultant of the 500 N force and • The positions of the two forces will be as shown in Fig. 2.10.7 (a). Example 2.10.8 The x component of a force Solution: • The x component of force is given 100 N. As x component is positive, it will be towards right as shown in Fig. 2.10.8 (a). • As line of action passes through B, the force can be either directed from A to B (i.e. second quadrant) or B to A (i.e. 4th quadrant). As Fx is towards right, the force has to be in 4th quadrant as shown in Fig. 2.10.8 (a). • The angle θ that Example 2.10.9 The 300 N horizontal force is to be replaced by two forces Solution: Example 2.10.10 Determine the angle θ(0°≤0≤ 90°) between the two forces so that the magnitude of the resultant force acting on the ring is minimum. What is the magnitude of the resultant force ? Refer Fig. 2.10.10. Solution: • The magnitude of resultant of two forces has maximum value when angle between them is 0°. As the angle is increased from 0° to 180°, the resultant magnitude goes on decreasing. As 0≤0≤90°, the magnitude of resultant will be minimum for Example 2.10.11 A tank is to be positioned in an excavation. Determine (α) The magnitude and direction of the smallest force P for which the resultant R of the two forces applied at A is vertical (b) The corresponding magnitude of R. Refer Fig. 2.10.11. Solution: Example 2.10.12 Two forces acting at a point have a maximum resultant of 2500 N and a minimum resultant of 1500 N. Determine the magnitudes of the two forces. Solution: Example 2.10.13 The sum of two concurrent forces P and Q is 500 N and their resultant is 400 N. If the resultant is perpendicular to P, find P, Q and angle between P and Q. Solution: Here we use parallelogram law. Refer Fig. 2.10.13. Let α be the angle between P and Q. Example 2.10.14 The resultant of two forces P and Q is R. If Q is doubled, the new resultant is observed to be perpendicular to P. Show that Q = R. Solution: Using parallelogram law, Example 2.10.15 Three forces act at a point O as shown in Fig. 2.10.14. Determine the magnitude and direction of a fourth force which when applied at O gives a resultant of 600 N at an angle of 30° in IVth quadrant. Solution: Whenever a vector in 2-D is unknown, assume it to be in first quadrant with components Fx and Fy in X and Y directions. After finding Fx and Fy, the magnitude and direction of F can be determined. As Fx is positive and Fy is negative force F acts is 4th quadrant. Example 2.10.16 Resolve a force of 100 N into two components of 200 N each. Show the orientation of these components on a sketch. Solution: • As all the magnitudes are known, to find the angleš, parallelogram law will be the most convenient method. • The 100 N force will be resultant of the two 200 N forces. ⸫ P = Q = 200 N; R = 100 N R2 = p2 + Q2 + 2 PQ cosα • The sketch will be as shown in Fig. 2.10.15 assuming one of the components to be horizontal. • When the two components of resultant are equal, it makes same angle with each force. Example 2.10.17 A collar that can slide on a vertical rod is subjected to the three forces shown. Determine a) The value of the angle a for which the resultant of the three forces is horizontal, b) The corresponding magnitude of the resultant. Solution: As the resultant is horizontal, Example 2.10.18 Two forces F1 = 500 N and F2 = 300 N are acting at point A as shown in Fig. 2.10.17. If the resultant of two forces has a magnitude of 750 N and acts vertically downward, determine the angle θ and ϕ. Solution: By parallelogram law, Example 2.10.19 Two forces are shown in Fig. 2.10.18. Knowing that the magnitude of P is 600 N, determine a) The required angle θ if the resultant R of the two forces is to be vertical, b) The corresponding value of R. Solution: As R is vertical, Example 2.10.20 Knowing that the tension in the cable BC is 145 N, determine the resultant of the three forces exerted at point 'B' of beam AB. Refer Fig. 2.10.19. Solution: The tension in cable BC is directed from B to C. Its angle with horizontal is θ. Example 2.10.21 Resolve the 60 N force into components acting along the u ant v axes and determine the magnitudes of the components. Refer Fig. 2.10.20. Solution: According to parallelogram law the two components Fu and Fv of force will be adjacent to the given force as shown in Fig. 2.10.20 (a). Choose x and y axes as shown. Example 2.10.22 The resultant of two forces P and Q is 1200 N vertical. Determine the force Q and the corresponding angle for the system of forces as shown in Fig. 2.10,21. Solution: As the resultant is 1200 N vertical, Example 2.10.23 The resultant of two forces P and Q is 1200 N horizontally leftward. Determine the force Q and the corresponding angle θ for the system of force s as shown in Fig. 2.13.22. Solution : Example 2.10.24 The angle between two concurrent forces is 90° and their resultant is 2500 N. The resultant makes an angle of 46° with one of the force. Determine the magntude of each force. Solution : As the angle between the two forces is 90°, the two forces are Example 2.10.25 Determine the magnitude of force P so that the resultant of the force system as shown in Fig. 2.10.24 is vertical and hence find magnitude of resultant force. Solution: As resultant is vertical, Example 2.10.26 Combine the two forces 800 N and 600 N, which act on the fixed dam structure at B, into a single equivalent force R if AC = 3 m, BC = 6 m and angle BCD = 60°. Refer Fig. 2.10.25. Solution : Refer Fig. 2.10.25 (a). Example 2.10.27 The force system shown in Fig. 2.10.26 have a resultant of 200 N along position Y axis, determine the magnitude and position θ of force F. Solution: Example 2.10.28 The post is to be pulled out of the ground using two ropes A and B as shown in Fig. 2.10.27. Rope A is subjected to a force of 600 N and is directed at 60° from the horizontal. If the resultant force acting on the post is be 1200 N vertically upward, determine the force T in rope B and the corresponding angle θ. Solution: As resultant force is 1200 N vertical, Example 2.10.29 The resultant of two forces P and Q is 1400 N vertical. Determine the force Q and the corresponding angle for the system of forces as shown in Fig. 2.10.28. Solution: As resultant is 1400 N vertical, Example 2.10.30 A trolley is acted upon by two forces as shown Fig. 2.10.30. If θ = 25° and the resultant R of the two forces is vertical, then determine the magnitude of the force P and resultant R. Solution: Assume R is vertically downwards. Example 2.10.31 Determine the magnitude and direction of the resultant of three forces acting on the book as shown in the Fig. 2.10.30. Solution: Example 2.10.32 Find the magnitude of the resultant of the coplanar forces 40 N, 30° and 70 N, 200° Solution: Example 2.10.33 Find the magnitude of the resultant of the two concurrent forces of magnitude 60 kN and 40 kN with an included angle 70° between them. Solution: Using parallelogram law, Example 2.10.34 Five forces act on a bolt 'B' as shown in Fig. 2.10.33. Determine the resultant of the forces on the bolt. Solution: Example 2.10.35 Determine the resultant of the concurrent force system shown in Fig. 2.10.34. Solution: Example 2.10.36 The truck is to be towed using two ropes. Determine the magnitudes of forces FA and FB acting on each rope in order to develop a resultant force of 950 N directed along the positive X-axis. Refer Fig. 2.10.35. Solution : Rx = 950 N Example 2.10.37 Two forces of magnitudes 1000 N and 400 N are applied as shown in Fig. 2.10.36. Find the direction in which a third force of magnitude 600 N must be applied to make the resultant of the three forces maximum. Also find the magnitude and direction of the resultant force. Solution: The magnitude of resultant force will be maximum if the third force of 600 N is applied in the direction of resultant of the remaining two forces. The resultant of 1000 N and 400 N can be obtained using parallelogram law. Let P = 400 N, Q = 1000 N, then α = 60° + 40° = 100° The resultant R1 is given by, As the third force of 600 N has to be applied in the direction of R1, the angle for the 600 N force is 37.1o in first quadrant. As 600 N and R1 are in same direction, the maximum magnitude of resultant of the three forces is 600 + R1 = 600 + 1010.5 = 1610.5 N Example 2.10.38 Solve example 2.10.37 if the resultant of the three forces is required to be minimum. Solution: The magnitude of resultant will be minimum if the third force of 600 N is applied opposite to the direction of resultant of the remaining two forces. Solving as in previous example, the resultant R1 of the 1000 N and 400 N forces is The resultant of the three forces is then R1 – 600 = 1010.5.- 600 = 410.5 N Example 2.10.39 Determine the magnitude of force F so that the magnitude of the resultant R of the three forces is as small as possible. What is the minimum magnitude of R. Refer Fig. 2.10.37. Solution: As there are three forces and their resultant, we have to use rectangular components. Example 2.10.40 A 200 N force is to be resolved into components along lines a-a' and b-b' as shown in Fig. 2.10.38. i) Determine the angle 'a' knowing that the component along a-a' is to be 150 N. ii) What is the corresponding value of the component along b-b'. Solution: The two components will be adjacent to the 200 N force. The 200 N force will be resultant of the two components Fa and Fb. The triangle of forces is as shown in Fig. 2.10.39 (a). Using sine rule, Example 2.10.41 A barge is pulled by two tugboats. If the resultant of the forces exerted by the tugboats is a 5000 N force directed along the axis of the barge, determine the value of a for which the tension in rope 2 is minimum. Solution: Let x-axis be directed along the barge and y-axis perpendicular to it. Then, ΣFx = 5000 N and ΣFy = 0 as the resultant force is along the axis. Using ΣFx = 5000 T1 cos 30 + T2 cos α = 5000 …(1) To get relation between T2 and α, we can get T1 from equation (2) and substitute in equation (1). Example 2.10.42 The following forces act at a point : i) 20 N inclined at 30° towards north of east ii) 25 N towards north iii) 30 N towards north west iv) 35 N inclined at 40° towards south of west. Find the magnitude and direction of resultant force. Solution: The four forces are as shown in Fig. 2.10.41. Example 2.10.43 The resultant of the forces system as shown in Fig. 2.10.42 is 520 N along the negative direction of y-axis. Determine 'P' and 'θ'. Solution: As resultant is 520 N along negative Y-direction, Rx = 0 and Ry = 520 N. Example 2.10.44 Four forces act on bolt A as shown. Determine the resultant of the forces on the bolt shown in Fig. 2.10.43. Solution: Example 2.10.45 Consider the 75-kg crate shown in the space diagram of Fig. 2.10.44. This crate was lying between two buildings and it is now being lifted onto a truck, which will remove it. The crate is supported by a vertical cable, which is joined at A to two ropes which pass over pulleys attached to the buildings at B and C. It is desired to determine the AU: Dec.-14, Marks 16 tension in each of the ropes AB and AC. Solution : The FBD of point A is shown in Fig. 2.10.44 (a). Using Lami's theorem, Example 2.10.46 Determine the stretch in each spring for equilibrium of the weight W = 40 N block as shown in Fig. 2.10.45. The springs are in equilibrium position. The stiffness of each spring is given as: k1= 40 N/m, k2 = 50 N/m and k3 = 60 N/m. Solution: The FBD of point C is shown in Fig. 2.10.45 (a). By Lami's theorem Example 2.10.47 A system of five forces of magnitude 4 kN, 5 kN, 6 kN, 7 kN and 8 kN acts at one of the angular points of a regular hexagon and the forces pass through the other angular points as shown in Fig. 2.10.46. Find the magnitude and direction of the resultant of the system of forces. Solution : Example 2.10.48 Two forces P and Q of magnitude 40 N and 60 N respectively act on a bolt A. Determine their resultant if P and Q makes 20° and 40° respectively with horizontal. Solution: Example 2.10.49 Two forces are applied to a hook support as shown in Fig.2.10.48. Knowing that magnitude of P is 35 N determine 1) The required angle a if the resultant R of the two forces applied to the support is to be horizontal 2) The corresponding magnitude of R. Solution: Example 2.10.50 A disabled automobile is pulled by means of two ropes as shown. Knowing that the tension in rope AB is 3750 N. Determine by trigonometry the tension in tope AC and the value of a. so that the resultant force exerted at A is a 6000 N force directed along the axis of the automobile. Solution: As resultant is horizontal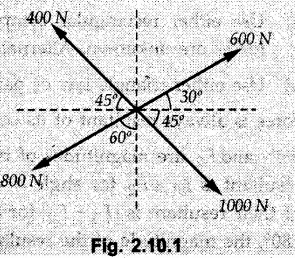



![]() , which together are equivalent to the action of the 1000 N force. Find the magnitude of
, which together are equivalent to the action of the 1000 N force. Find the magnitude of ![]() and the angle α that it makes with the Y axis.
and the angle α that it makes with the Y axis.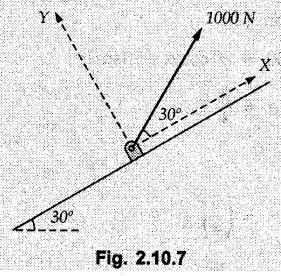
![]() and hence has to lie between the two forces on that side where the angle between them is less than 180°.
and hence has to lie between the two forces on that side where the angle between them is less than 180°.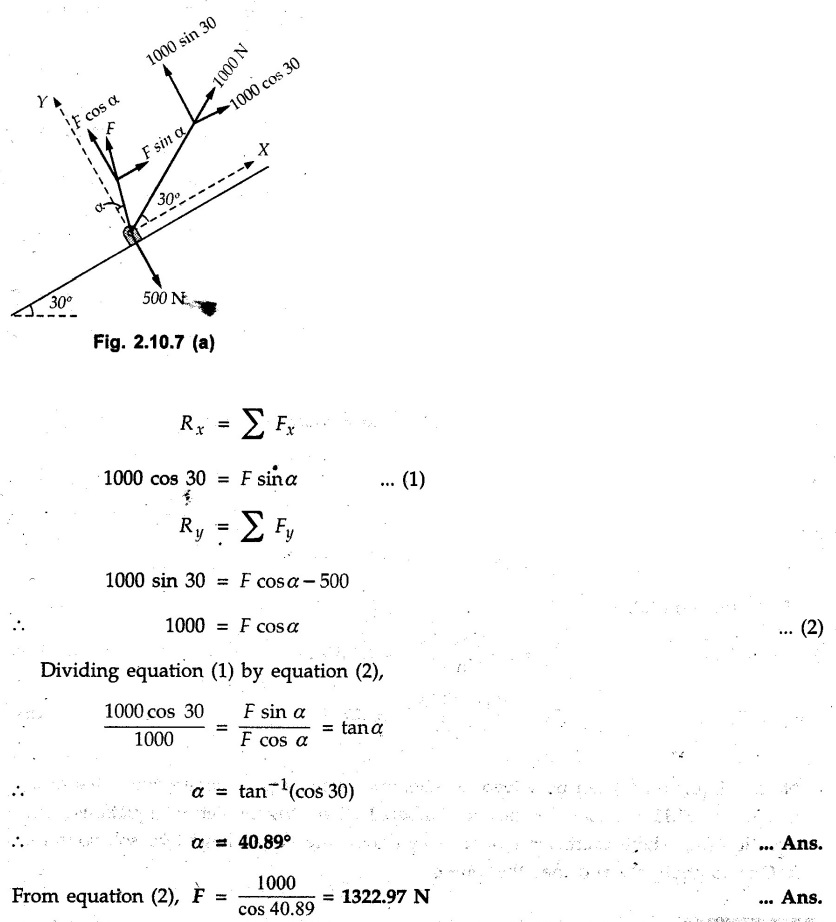
![]() applied on a rectangular plate at A is 100 N. If the line of action of
applied on a rectangular plate at A is 100 N. If the line of action of ![]() passes through B, determine the magnitude of
passes through B, determine the magnitude of ![]() and its y component. Refer Fig. 2.10.8.
and its y component. Refer Fig. 2.10.8.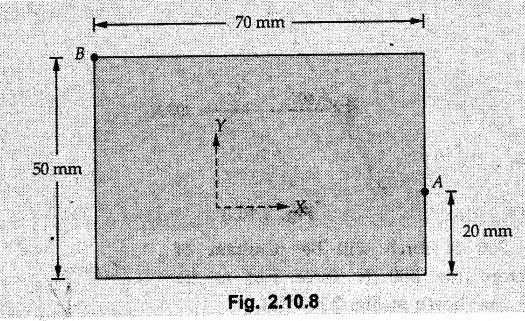
![]() makes with horizontal is given by,
makes with horizontal is given by,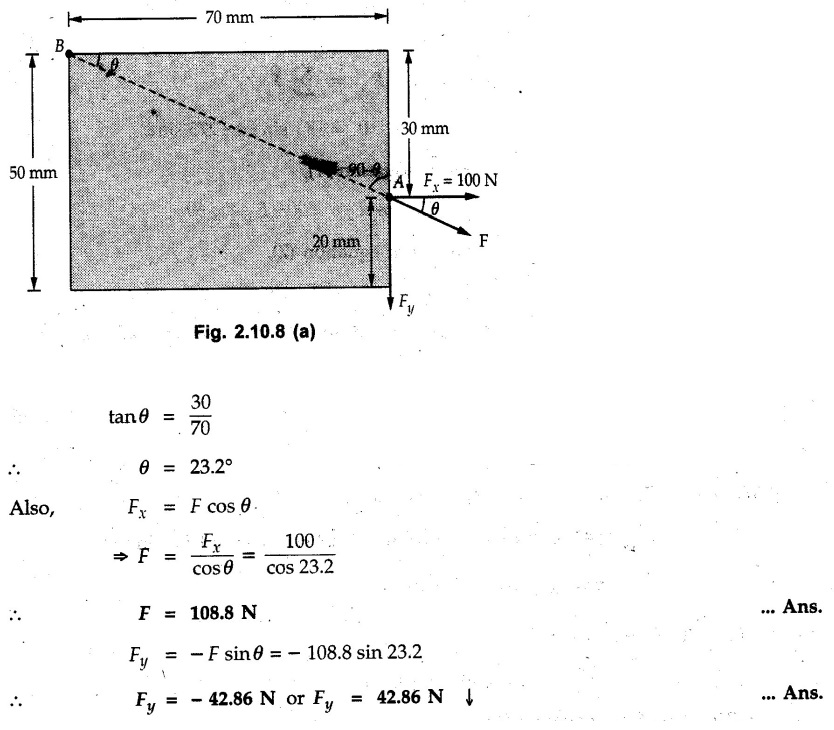
![]() , directed along axis a-a and
, directed along axis a-a and ![]() which has magnitude of 275 N. Determine the magnitude of
which has magnitude of 275 N. Determine the magnitude of ![]() and the axis a-a a angle a which F2 makes with the horizontal. Refer Fig. 2.10.9.
and the axis a-a a angle a which F2 makes with the horizontal. Refer Fig. 2.10.9.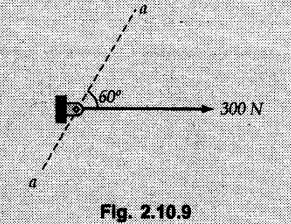



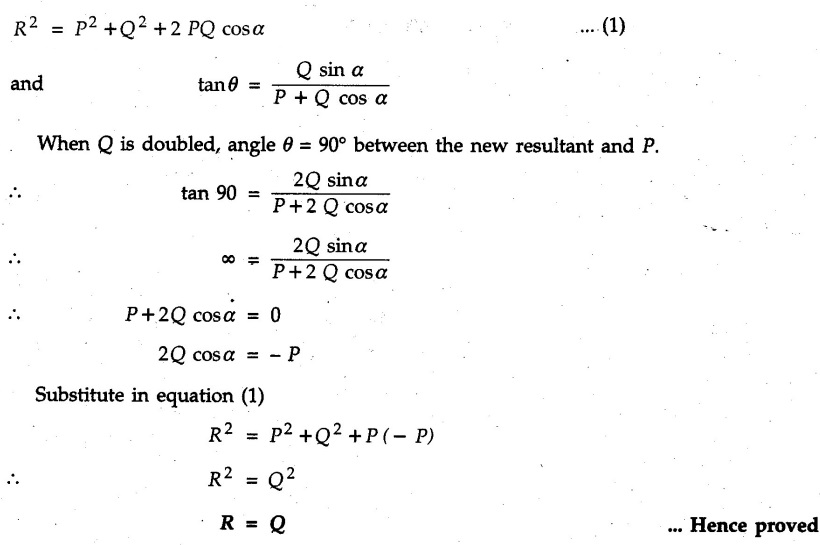







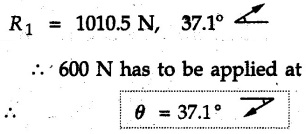

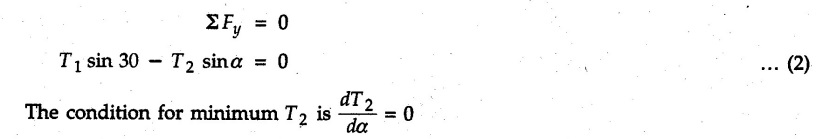






Engineering Mechanics: Unit I: Statics of Particles : Tag: : - Solved Example & Practice Problems: Magnitude of resultant
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
