Solved Example & Practice Problems: Ladder Friction

Ladder Friction

Solved Examples for Understanding

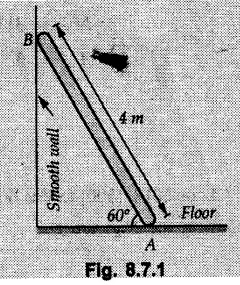
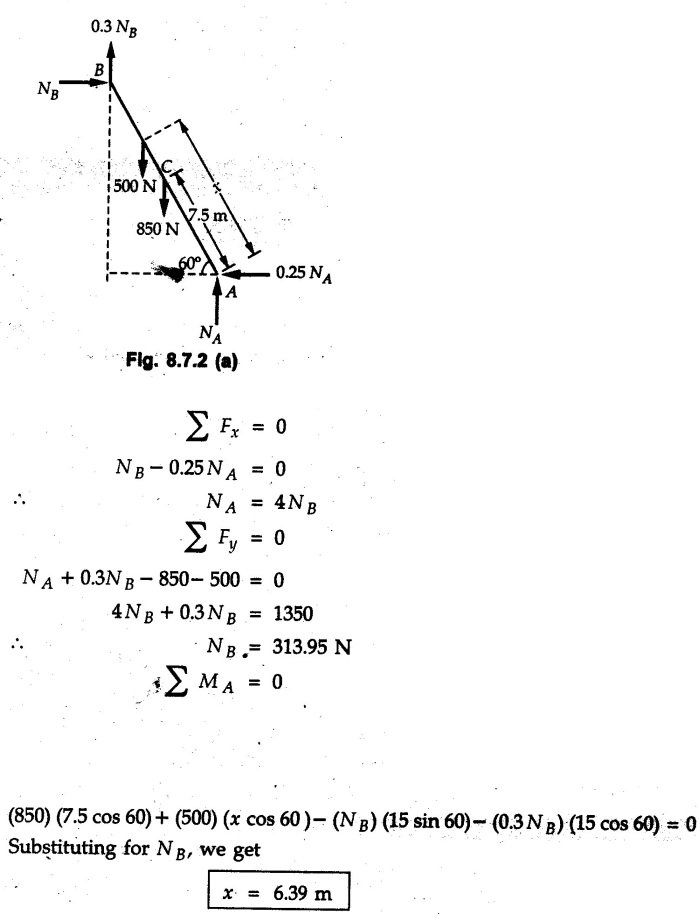
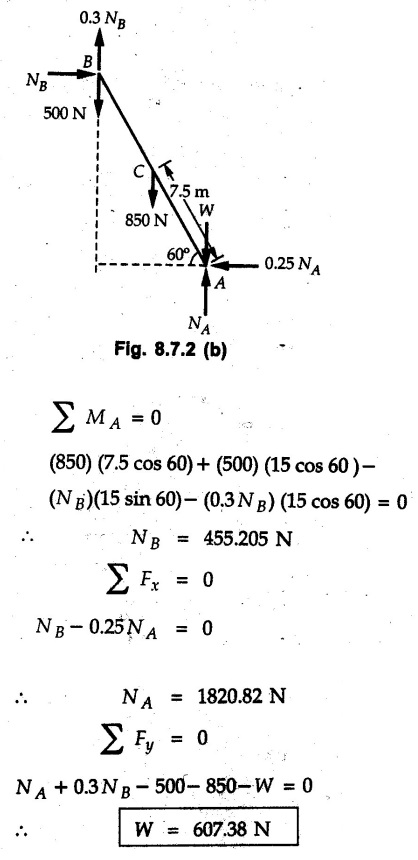
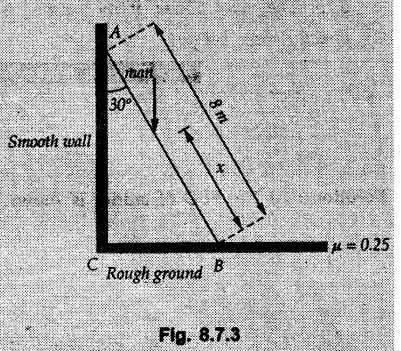
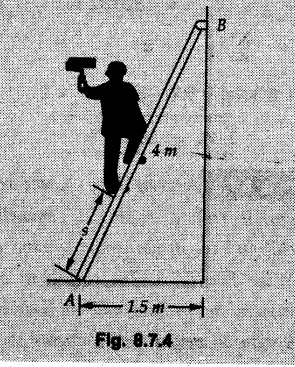
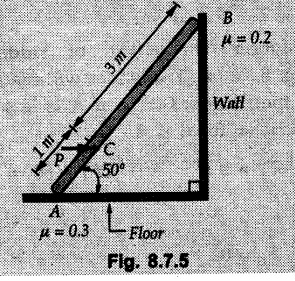
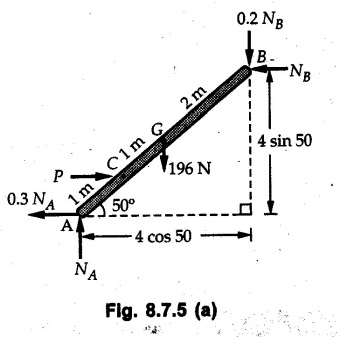
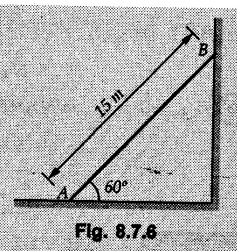
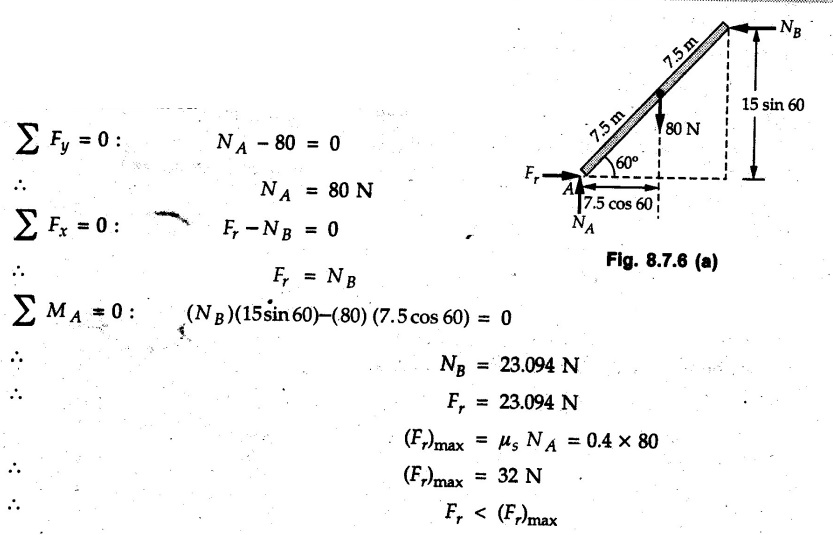
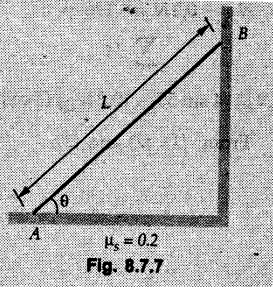
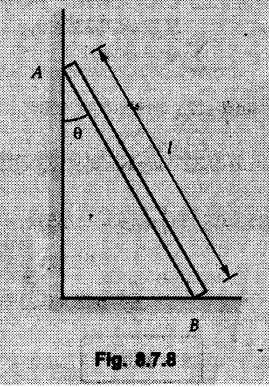
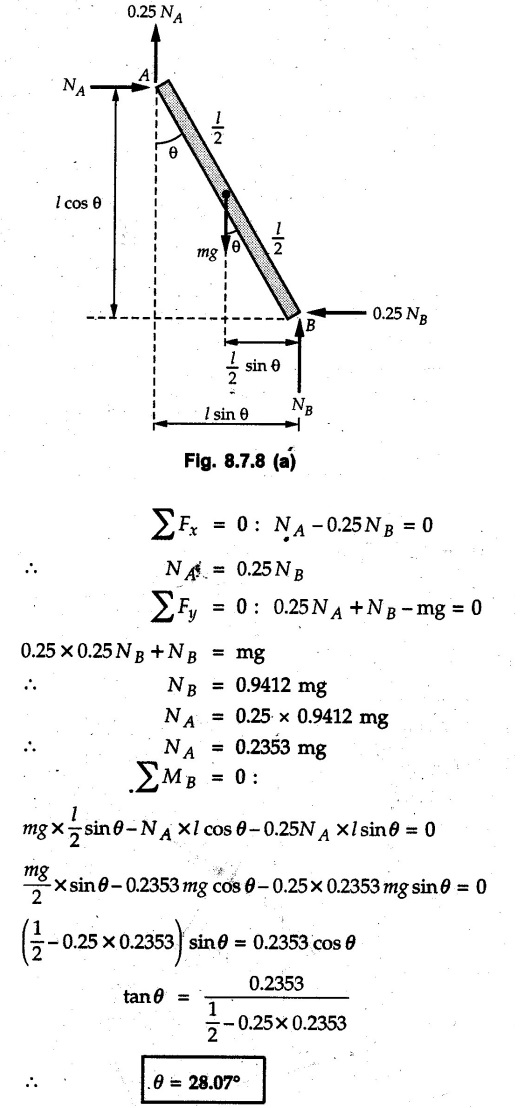
Example 8.7.1 

A ladder of weight 1000 N and length 4 m rests as shown in Fig. 8.7.1. If a 750 N weight is applied at a distance of 3 m from the top of ladder, it is at the point of sliding. Determine the coefficient of friction between ladder and the floor.

Solution: 

The F.B.D of ladder is shown in Fig. 8.7.1. (a)

Example 8.7.2

 A uniform ladder of length 15 m rests against a vertical wall making an angle of 60° with the horizontal. Coefficient of friction between wall and the ladder is 0.30 and between the ground and the ladder is 0.25. A man weighing 500 N ascends the ladder. How long will he be able to go before the ladder slips? Find the weight that is necessary to be put at the bottom of the ladder so as to be just sufficient to permit the man to go to the top. Assume weight of the ladder to be 850 N. 

Solution: 

The F.B.D. of ladder is shown in Fig. 8.7.2 (a).

The F.B.D. of ladder when weight W is put at the bottom is shown in Fig. 8.7.2 (b).

Example 8.7.3

A weightless ladder, of length 8 m, is resting against a smooth vertical wall and rough horizontal ground as shown in the Fig. 8.7.3. The coefficient of friction between the ground and the ladder is 0.25. A man of weight 500 N wants to climb up the ladder. Find how much distance along the ladder the man can climb without slip. A second person weighing 800 N wants to climb up the same ladder. Would he climb less than the earlier person? Find his distance covered.

Solution : 

Consider weight of the man to be W( which can be substituted later as either 500 N or 800 N). The F.B.D. of ladder is shown in Fig. 8.7.3 (a).

As this distance does not depend on W, both the persons will be able to climb the same distance.

Example 8.7.4 

Determine the distance s to which the 90 kg painter can climb without causing the 4-m ladder to slip at its lower end A Fig. 8.7.4. The top of the 15 kg ladder has a small roller and at the ground the coefficient of static friction is 0.25. The mass center of the painter is directly above her feet.

Solution: 

(i) The FBD of ladder is shown in Fig. 8.7.4 (a).

Example 8.7.5 

A ladder AB weighing 196 N is resting against a rough wall and a rough floor, as shown in Fig. 8.7.5. Calculate the minimum horizontal force 'P' required to be applied at C in order to push the ladder towards the wall. Assume coefficient of friction at A = 0.3 and that B = 0.2.

Solution : 

The F.B.D. of ladder is shown in Fig. 8.7.5 (a).

There are three unknowns - P, NA and NB which can be obtained using the three equations

Example 8.7.6 

The 15 m ladder has a uniform weight of 80 N and rest against the smooth wall at B as shown in Fig. 8.7.6. If the coefficient of static friction μs = 0.4, determine if the ladder will slip ?

Solution: 

The F.B.D. of ladder is shown in Fig. 8.7.6 (a). The ladder will remain in equilibrium if the frictional force at A is less than the limiting frictional force at A.

⸫ The ladder will not slip.

Example 8.7.7 

The uniform rod having a weight W and length L is supported at its ends A and B as shown in Fig. 8.7.7, where the coefficient of static friction μs = 0.2. Determine the greatest angle e so that the rod does not slip.

Solution: The FBD of rod is shown in Fig. 8.7.7 (a).

Example 8.7.8 

A uniform pole of length 1 and mass m in leaned against the vertical wall as shown in Fig. 8.7.8. If the coefficient of static friction between supporting surfaces and the ends of the pole is 0.25, calculate the maximum angle 0 at which the pole may place before it starts to slip.

Solution: 

The FBD of pole is shown in Fig. 8.7.8 (a).

Examples for Practice

Q.1 

A uniform ladder 3 m long and weighing 300 N is placed against a wall making an angle of 60° with the ground. The ladder in addition to its own weight has to support a 800 N weight of a man standing at its upper end. Assuming the coefficient of friction between the wall and ladder is 0.30 and that between the ground and ladder is 0.40 find the horizontal force 'P' to be applied at ground level to prevent slipping. If the force 'P' is not applied, what should be the minimum inclination of the ladder with the horizontal so that there is no slipping of it with the man standing at its upper end? 

[Ans. : P = 83.61 N, θ= 64.73° ]

Q.2

A uniform ladder of weight 850 N and length 6 m rests on a horizontal ground and leans against a smooth vertical wall. The angle made by the ladder with the horizontal is 65°. When a man of weight 700 N stands on the ladder at a distance of 4 m from the top of the ladder, the ladder is at the point of sliding. Determine the coefficient of friction between the ladder and the floor. 

[Ans. : μ = 0.198]

Q.3

A ladder 5 m long, weighing 250 N is resting against a wall at an angle of 60° with the horizontal floor. A man weighing 750 N climbs the ladder. At what position along the ladder from the bottom does he induce slipping? The coefficient of friction between wall and ladder as well as floor and ladder is 0.3. 

[Ans. : 2.895 m]