Engineering Mechanics: Unit IV: Friction
Solved Example & Practice Problems: Dry Friction
Solved Example Problems, Examples for Practice: Dry Friction - Friction - Engineering Mechanics
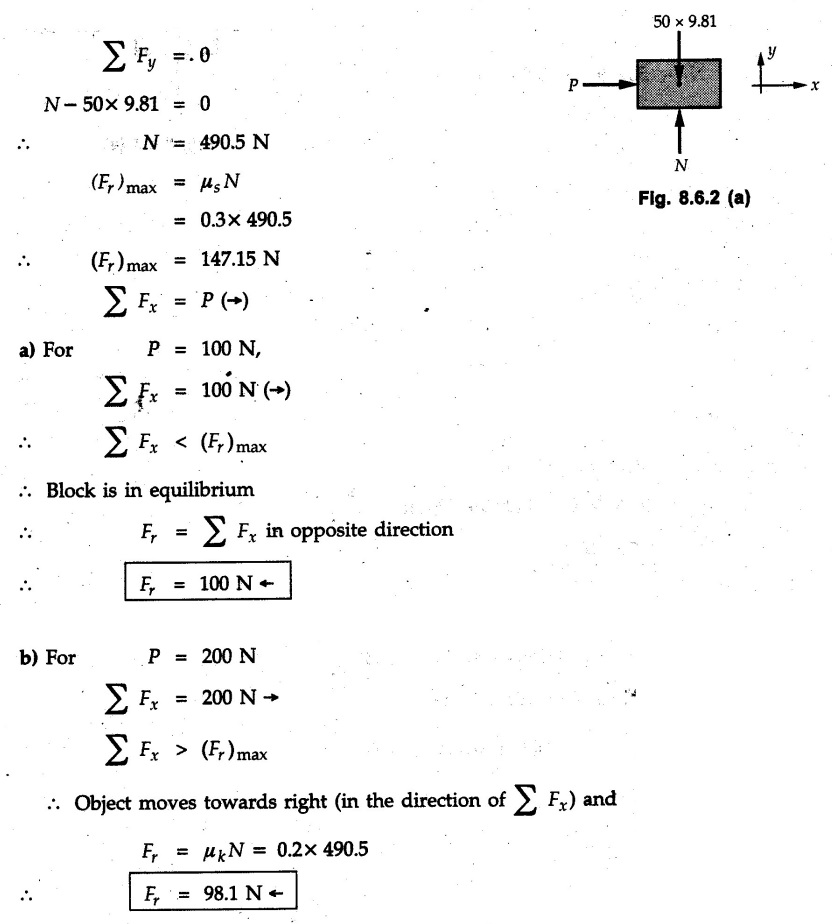
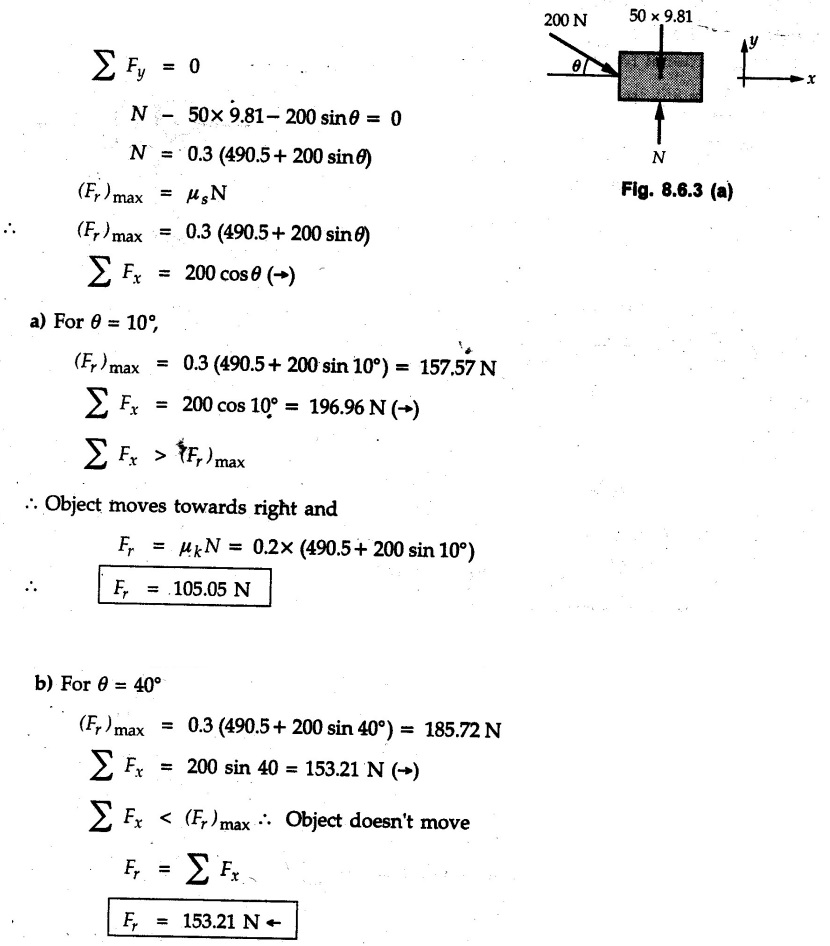
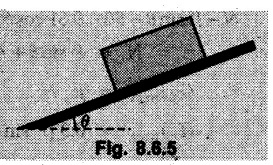
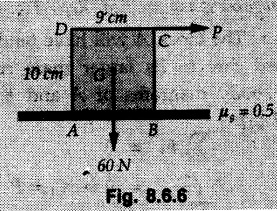
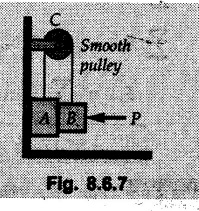
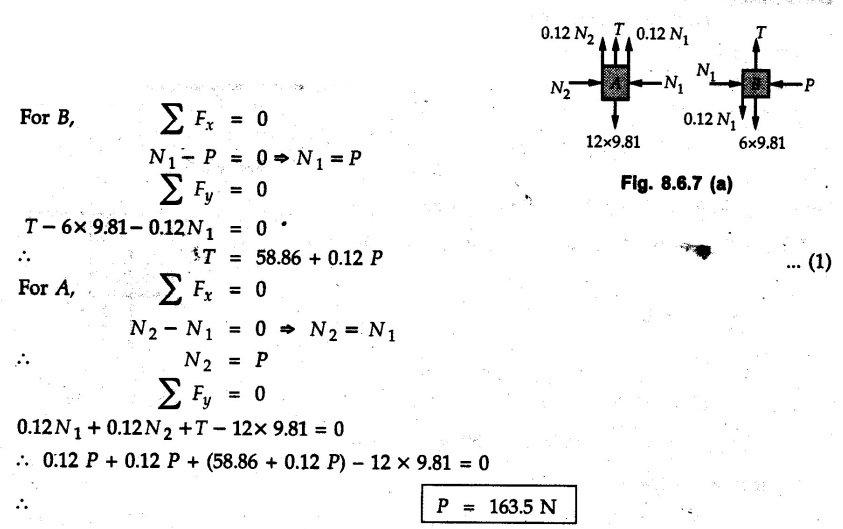
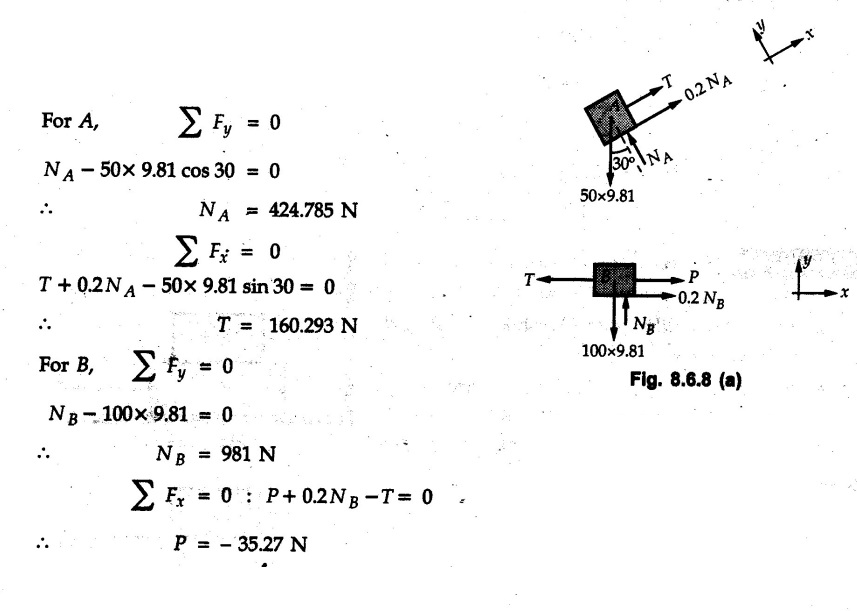
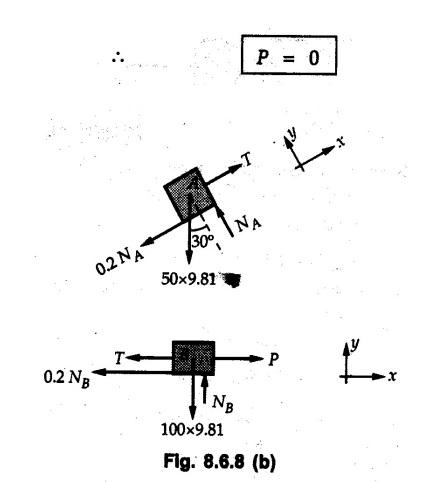
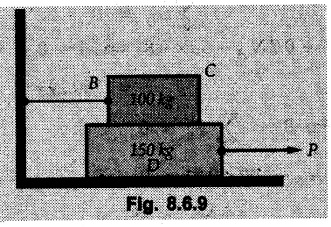
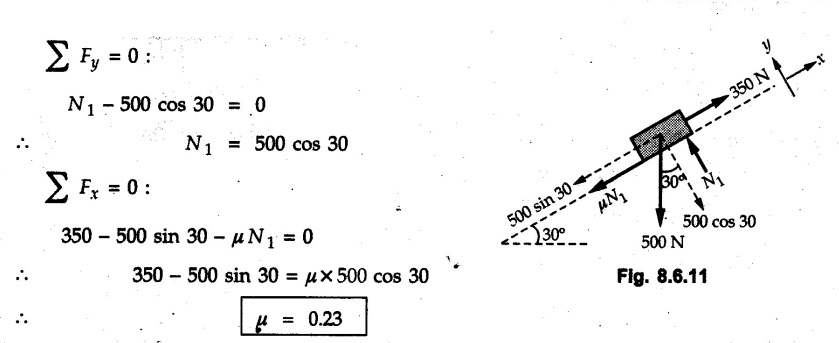
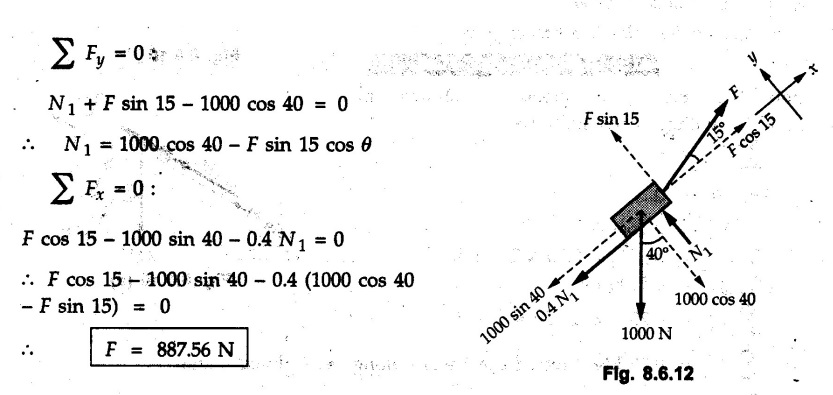
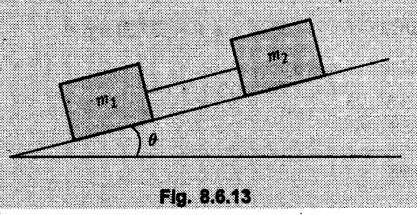
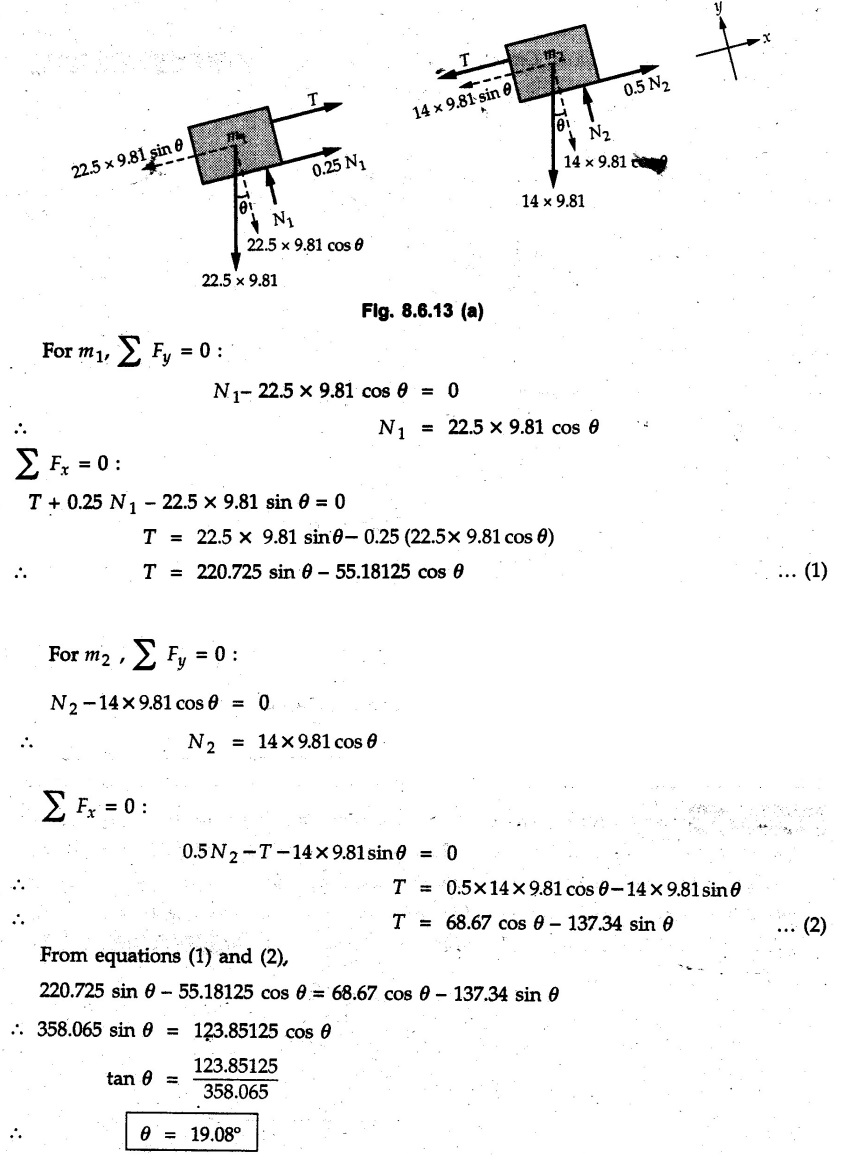
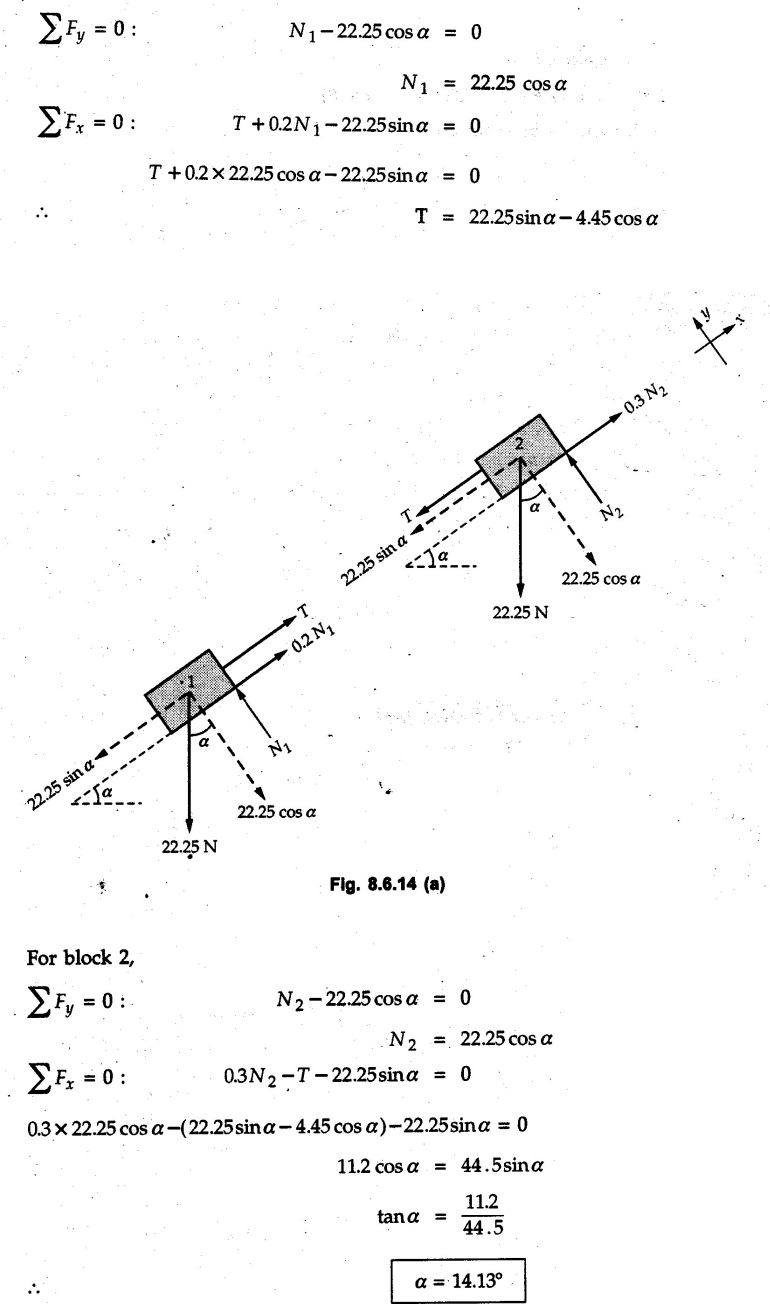
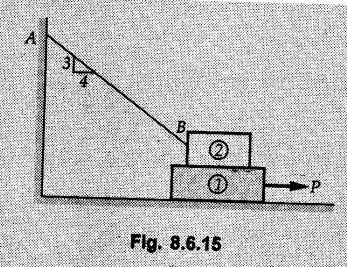
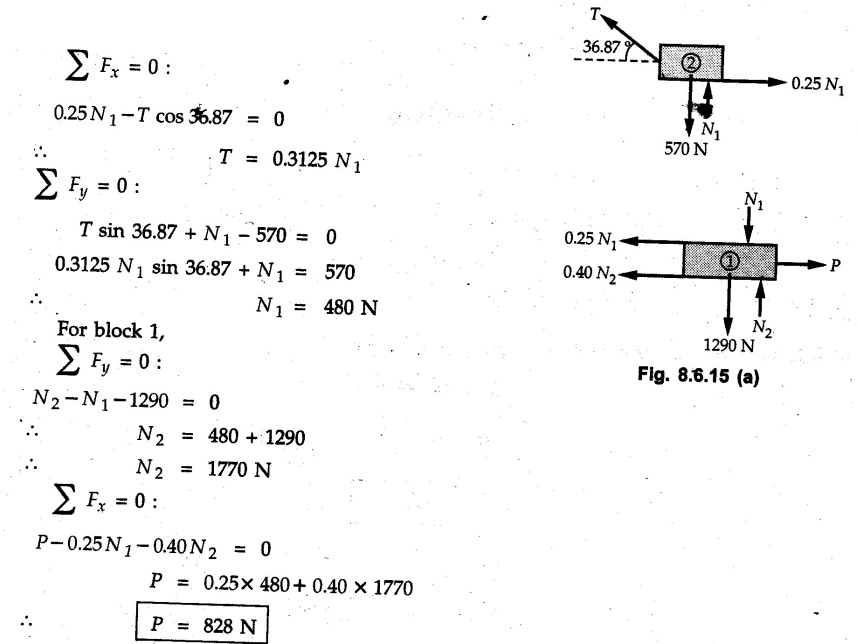
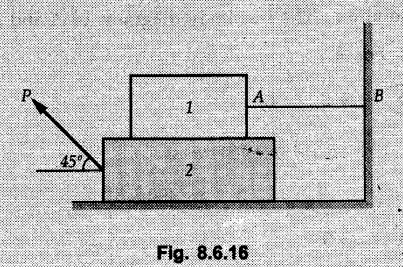
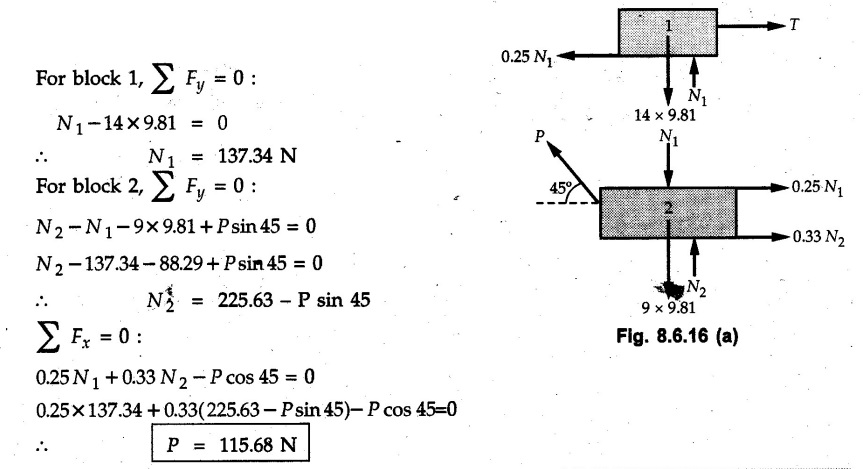
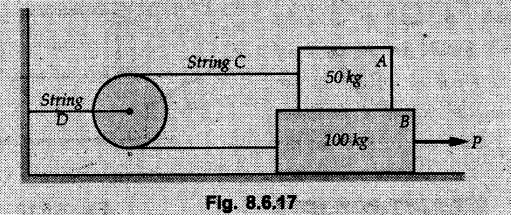
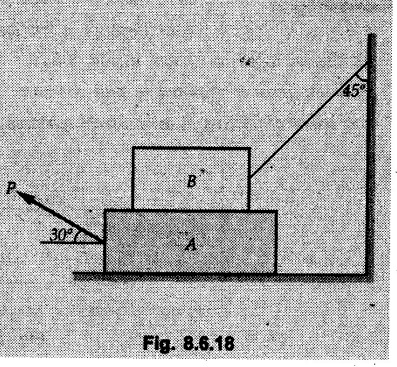
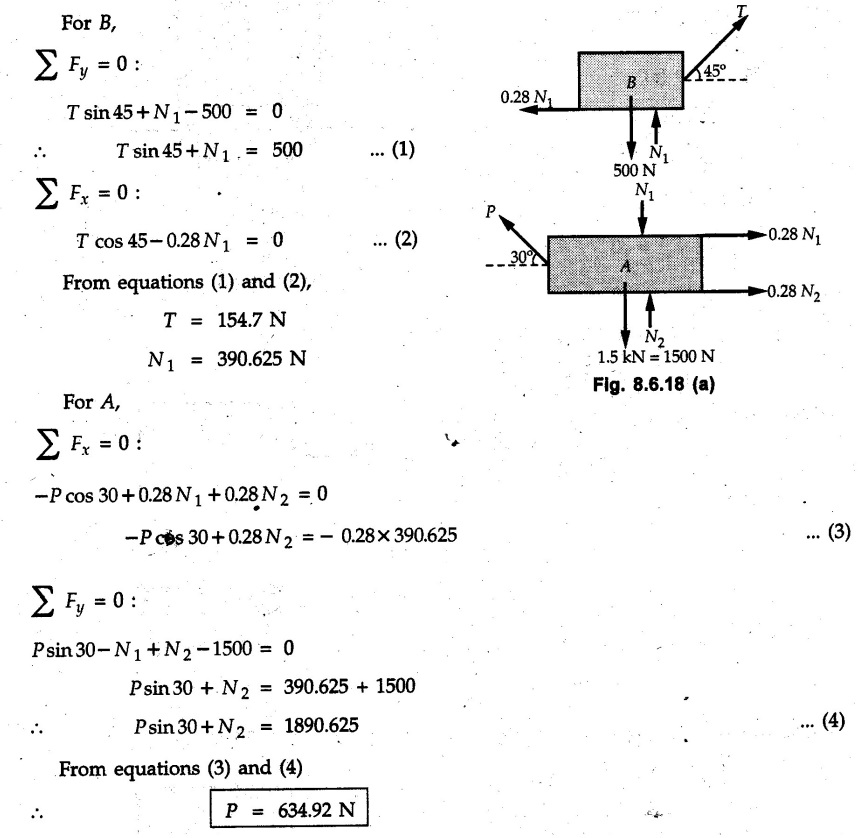
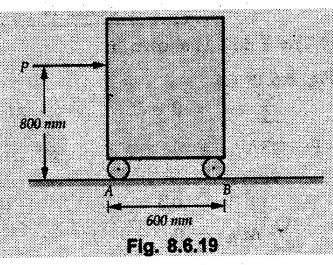
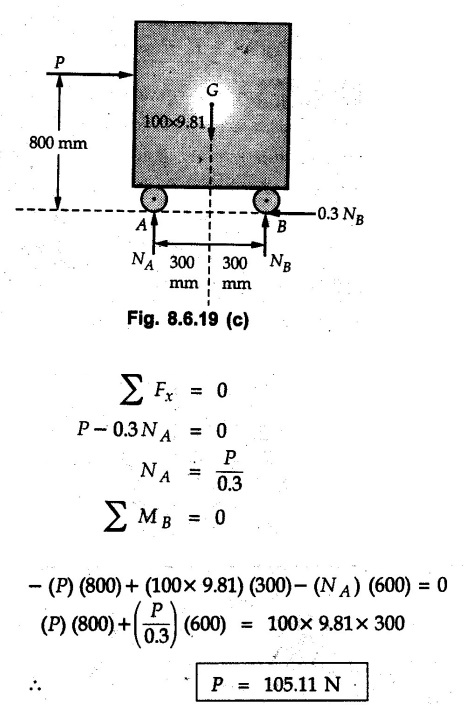
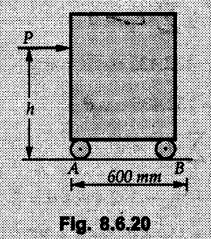
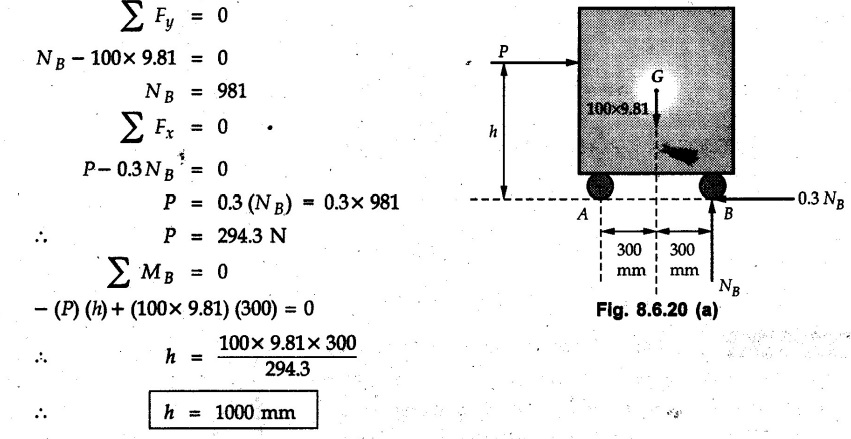
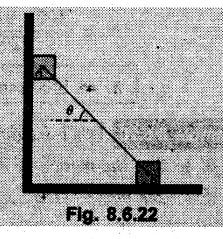
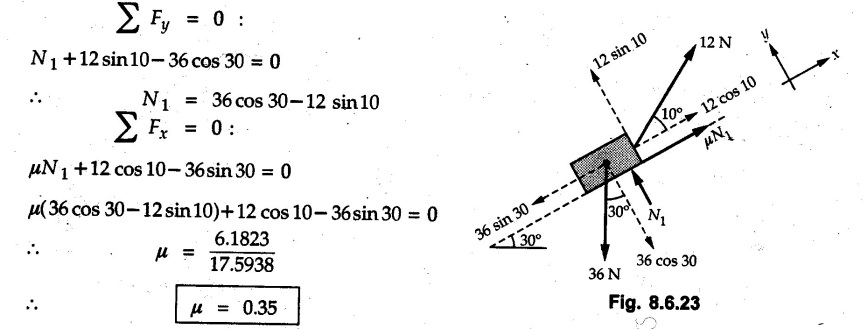
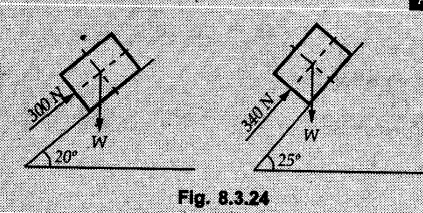
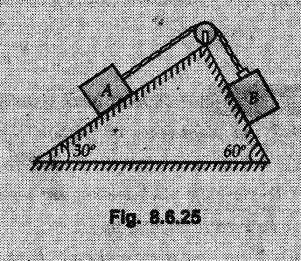
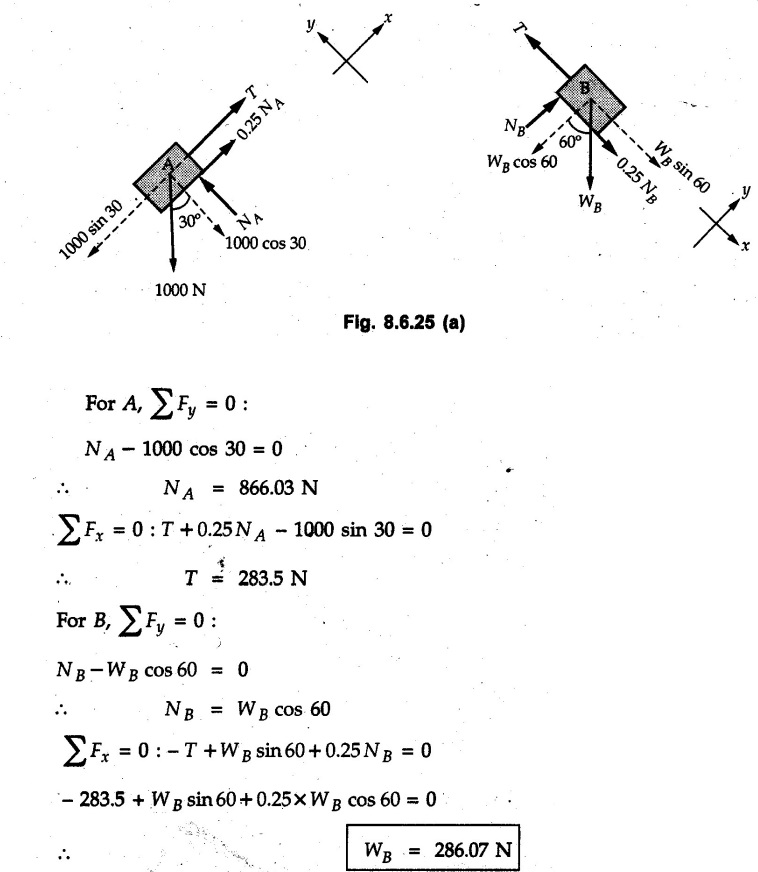
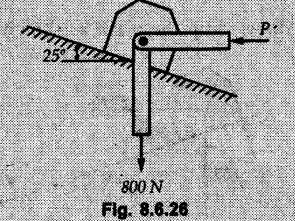
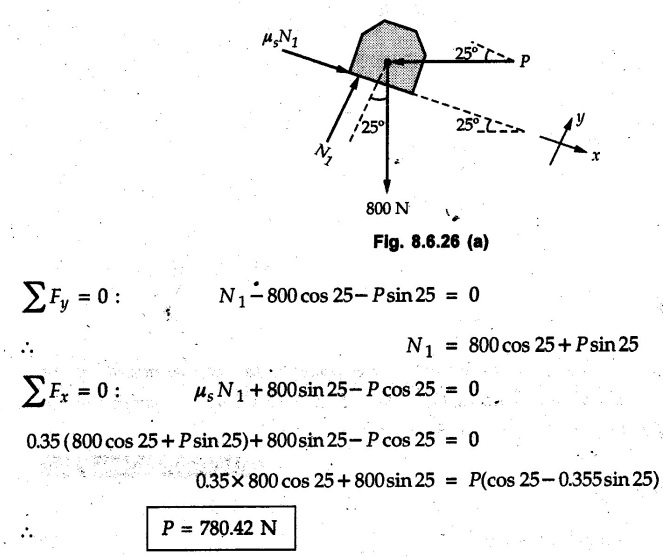
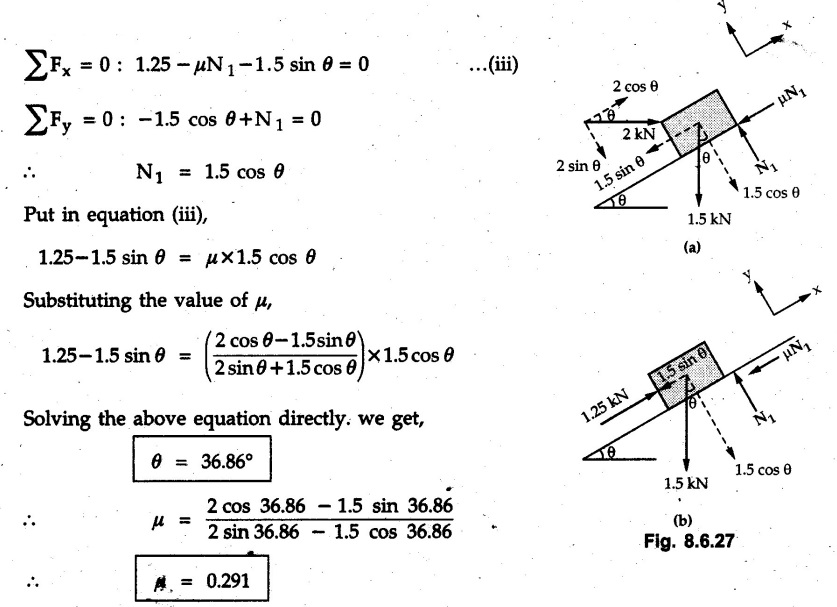
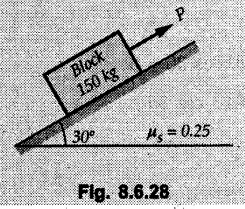
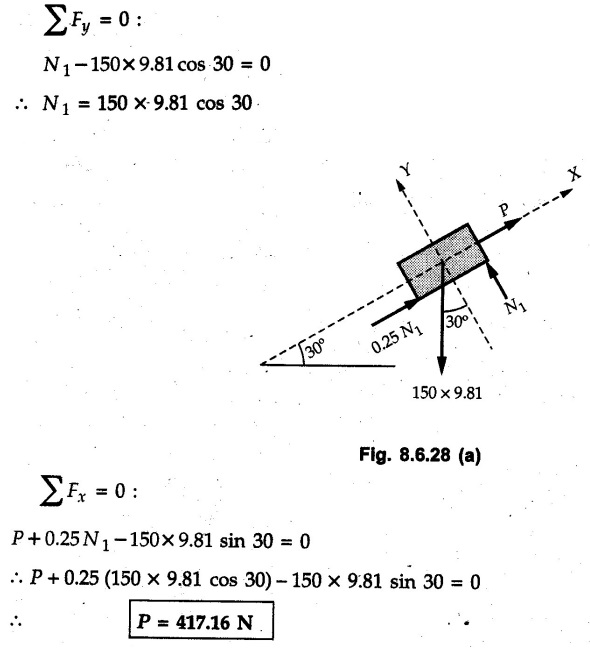
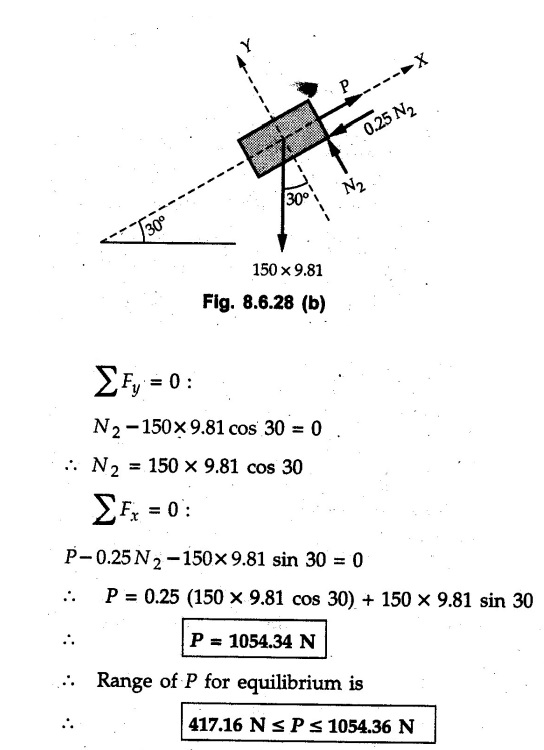
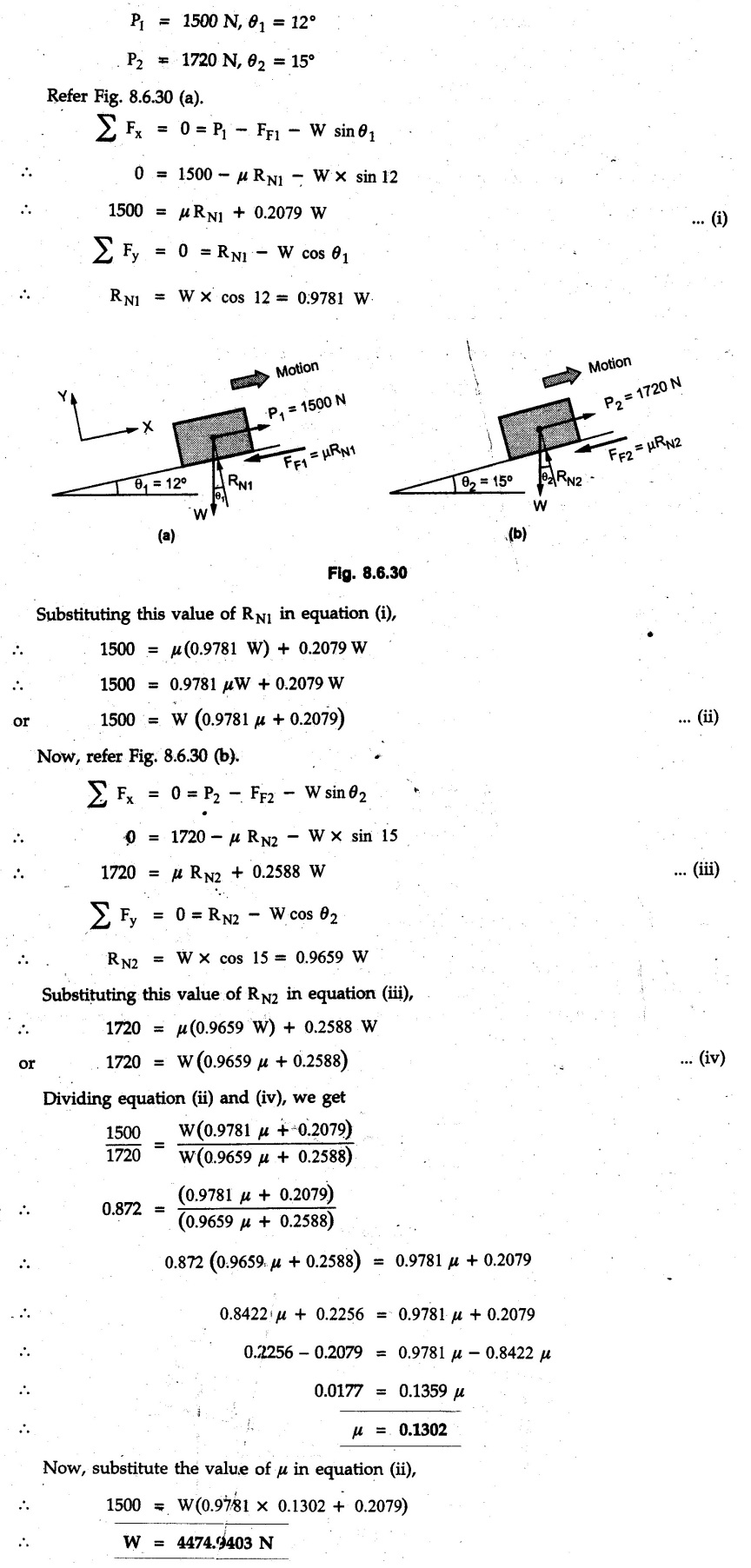
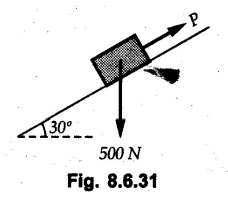
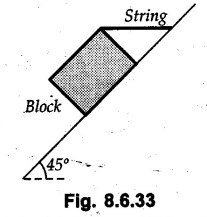
Dry Friction Solved Examples for Understanding Example 8.6.1 Determine whether the 50 kg block shown in Fig. 8.6.2 is in equilibrium and find the magnitude and direction of the frictional force when a) P = 100 N and b) P 200 N. Take μs = 0.3 and μk = 0.2. Solution: The F.B.D. of block is shown in Fig. 8.6.2 (a) excluding frictional force. Example 8.6.2 Determine whether the 50 kg block shown in Fig. 8.6.3 is in equilibrium and find the magnitude and direction of the frictional force when a) θ = 10° and b) θ = 40°. Take μs = 0.3 and μk = 0.2. Solution: The F.B.D. of block is shown in Fig. 8.6.3 (a) without frictional force. Example 8.6.3 Determine whether the 50 kg block shown in Fig. 8.6.4 is in equilibrium and find the magnitude and direction of the frictional force when a) P = 200 N, θ =20° b) P = 200 N, θ = 45° c) P = 100 N, θ = 20°. μs = 0.3 and μk = 0.2. Solution: The F.B.D. of block is shown in Fig. 8.6.3 (a) without frictional force Example 8.6.4 Determine whether the 50 kg block shown in Fig. 8.6.5 is in equilibrium and find the magnitude and direction of the frictional force, a) θ = 20° b) θ = 10°. Take μs =0.3 and μk = 0.2. Solution: This problem can be solved easily using the concept of angle of friction. The angle of friction. The angle of repose is same as angle of friction. Hence object will slide down if the angle θ is greater than ϕs = 16.7°. Example 8.6.5 For the block shown in Fig. 8.6.6, find the minimum value of 'P which will just disturb the equilibrium of the system. Solution: The block will have sliding motion if P > (Fr)max. From F.B.D. of block shown in Fig. 8.6.6 (a) without frictional force, From equations (1) and (2), the smallest value of P for which equilibrium is disturbed is Example 8.6.6 Blocks A and B of masses 12 kg and 6 kg respectively are connected by light inextensible cable passing over frictionless pulley C which can rotate freely. If μs = 0.12 for all surfaces in contact, determine smallest value of P for which equilibrium is maintained. Refer Fig. 8.6.7. Solution: The block A will have tendency to move downward due to its larger mass compared to B. The free body diagrams of A and B are shown in Fig. 8.6.7 (a). Example 8.6.7 Two blocks A and B having masses 50 kg and 100 kg respectively are connected by a string which passes over frictionless pulley as shown in Fig. 8.6.8. Coefficient of friction between block and surface is 0.2 for both A and B. Determine force P if, a) The system is prevented to move towards left. b) The system is just on the point of moving towards right. Solution: a) For impending motion towards left, the free body diagram of A and B are shown in Fig. 8.6.8 (a). Negative value of P indicates that the system will not be able to move towards left even if left to itself making P equal to zero. b) For impending motion of the system towards right, the free body diagrams of A and B are shown in Fig. 8.6.8 (b). Example 8.6.8 The coefficients of friction are μ, = 0.3 and μk = 0.25 between all surfaces of contact. Determine the smallest force P required to just start block D moving if a) Block C is restrained by cable AB as shown. b) Cable AB is removed. Refer Fig. 8.6.9. Solution: As there is only impending motion, (i.e. actual motion does not take place), we have to use μs. a) F.B.D. of blocks are shown in Fig. 8.6.9 (a) when block C is restrained by cable AB. Example 8.6.10 A body of weight 500 N is pulled up an inclined plane, by a force of 350 N. The inclination of the plane is 30° to the horizontal and the force is applied parallel to the plane. Determine the coefficient of friction. Solution: The F.B.D. is shown in Fig. 8.6.11. Example 8.6.11 A block weighing 1000 N is kept on a rough plane inclined at 40° to the horizontal. The coefficient of friction between the block and the plane is 0.4. Determine the smallest (least) force inclined at 15° to the plane required just to move the block up the plane. Solution: The F.B.D. of the block is shown in Fig. 8.6.12. Example 8.6.12 Two masses my and my are tied together by a rope parallel to the inclined plane surface as shown in Fig. 8.6.13. Their masses are 22.5 kg and 14 kg respectively. The co-efficient of friction between m1 and the plane is 0.25 while that of mass m2 and the plane is 0.5. Determine ) The value of the inclination of the plane surface, θ for which the masses will just start sliding ii) The tension in the rope. Solution: The free body diagrams of the two masses are shown in Fig. 8.6.13 (a). Example 8.6.13 Two blocks of weight W1 and W2 rest on a rough inclined plane Fig. 8.6.14 and are connected by a short piece of string as shown in Fig. 8.6.14. If the coefficients of friction are μ1 = 0.2 and μ2 = 0.3, respectively, find the angle of inclination of the plane μ2 for which sliding will impend. Given: W1 = W2 = 22.25 N. Solution: The two free body diagrams are shown in Fig. 8.6.14 (a). For block 1, Example 8.6.14 A block of weight W1 = 1290 N rests on a horizontal surface and supports another block of weight W2 = 570 N on top of it as shown in Fig. 8.6.15. Block of weight W2 is attached to a vertical wall by an inclined string AB. Find the force P applied to the lower block, that will be necessary to cause the slipping to impend. Coefficient of friction between blocks 1 and 2 = 0.25 Coefficient of friction between 1 1 and horizontal surface = 0.40. Solution: The two free body diagrams are shown in Fig. 8.6.15 (a). For block 2, Example 8.6.15 Block (2) rests on block (1) Friction and is attached by horizontal rope AB to the wall as shown in Fig. 8.6.16. What force P is necessary to cause motion of block (1) to impend? The co-efficient of friction between the block is 0.25 and between the floor and block (1) is 0.33. Mass of blocks (1) and (2) are 14 kg and 9 kg respectively. Solution: The free body diagrams of the two blocks are shown in Fig. 8.6.16 (a). Example 8.6.16 Two blocks A and B of mass 50 kg and 100 kg respectively are connected by a string C which passes through a frictionless pulley connected with the fixed wall by another string D as shown in Fig. 8.6.17. Find the force P required to pull the block B. Also find the tension in the string D. Take coefficient of friction at all contract surfaces as 0.3. Solution: The free body diagrams of A and B are shown in Fig. 8.6.17 (a). Example 8.6.17 Block 'A' weighing 1.5 kN rests on a horizontal plane and supports another block weighing 500 N on to of it as shown in Fig. 8.6.18. The block B is attached to a vertical wall by an inclined string, which makes an angle of 45° with the vertical. What should be the value of force P acting at an angle of 30° to the horizontal to cause the motion of the lower block to impend? Take μ = 0.28 for all the surfaces. Solution: The free body diagrams of the two blocks are shown in Fig. 8.6.18 (a). Example 8.6.18 A 100 kg cupboard is mounted on small caster wheels which can be locked to prevent their rotation. If μs = 0.3 between wheels and floor, determine 'P' to move cupboard to the right when (a) All casters are locked (b) Only casters at B are locked (c) Only casters at A are locked. Refer Fig. 8.6.19, Solution: If casters are not locked, there will be no frictional force as rolling friction is negligible. a) The F.B.D. of cupboard is shown in Fig. 8.6.19 (a). b) As casters at B are locked, there will be frictional force at B and 0 friction at A as these casters are free to roll. The F.B.D. is shown in Fig. 8.6.19 (b). c) The F.B.D. is shown in Fig. 8.6.19 (c) Example 8.6.19 A 100 kg cupboard is mounted on small caster wheels which are locked to prevent their rotation. If μs = 0.3 between wheels and floor, determine the maximum height 'h' at which the force 'P' can be applied to move cupboard to the right. Refer Fig. 8.6.20. Solution: The F.B.D. of cupboard is shown in Fig. 8.6.20 (a). For maximum 'h', NA → 0. Example 8.6.20 What should be the value of 6' so that the motion of block 'A' impends down the plane? The coefficient of friction ‘μ' for all the surfaces is 1/3. Refer Fig. 8.6.21. Solution: The free body diagrams of A and B are shown in Fig. 8.6.21 (a). Example 8.6.21 Two identical blocks A and B are connected by rod and rest against vertical and horizontal planes respectively as shown in the Fig. 8.6.22. If sliding impends when θ = 45°, determine the coefficient of friction μ assuming it to be the same at both floor and wall. Solution: The free body diagrams of A and B are shown in Fig. 8.6.22 (a). The weight of each block is assumed to be W. Example 8.6.22 A block weighing 36 N is resting on the rough inclined plane having an inclination of 30°. A force of 12 N is applied at an angle of 10° up the plane and the block is just on the point of moving down the plane. Determine the coefficient of friction. Solution: The functional block diagram of block is shown in the Fig. 8.6.23. Example 8.6.23 A force of 300 N is required just to move a block up a plane inclined at 20° to the horizontal, the force being applied parallel to the plane Fig. 8.6.24. If the inclination of the plane is increased to 25°, the force required just to move the block up is 340 N, (the force is acting parallel to the plane). Determine the weight of the block and the coefficient of friction. Solution: The two free body diagrams are shown in Fig. 8.6.24 (a). Example 8.6.24 Two blocks A and B are placed on inclined planes as shown in Fig. 8.6.25. The block A weighs 1000 N. Determine minimum weight of the block B for maintaining the equilibrium of the system. Assume that the blocks are connected by an inextensible string passing over a frictionless pulley. Co efficient of friction μA between the block A and the plane is на 0.25. Assume the same value for μB. Solution: For minimum weight of B, the block A has tendency to slide down. The free body diagrams of A and B are shown in Fig. 8.6.25 (a). Example 8.6.25 A support block is acted upon by two forces as shown in Fig.8.6.26. Knowing that the coefficients of friction between the block and the incline are μs = 0.35 and μk = 0.25, determine the force P required i) To start the block moving up the incline, i) To keep it moving up, in) To prevent it from sliding down. Solution: i) The FBD of block is shown in Fig. 8.6.26 (a). ii) The FBD is some as for part (i) except that μs is replaced by μk. iii) The frictional force is directed up the plane as shown in Fig. 8.6.26 (b). Example 8.6.26 A load of 1.5 kN, resting on an inclined rough plane, can be moved up the plane by a force of 2 KN applied horizontally or by a force 1.25 kN applied parallel to the plan. Find the inclination of plane and coefficient of friction. Solution: For Fig.8.6.27 (a) Put in equation (ii), 2 cos θ - 1.5 sin θ = μ (2 sin θ + 1.5 cos θ) For Fig. 8.6.27 (b) Example 8.6.27 A block of mass 150 kg is resting on a plane inclinded at 30° with horizontal shown in Fig. 8.6.28. Determine range of an external force P to maintain equilibrium. Assume μs = 0.25. Solution: (a) For minimum value of P, the block has tendency to slide down the plane. Hence the frictional force is directed up the plane. The F.B.D. of block for this situation is shown in Fig. 8.6.28 (a). (b) For maximum value of P, the block has tendency to slide up the plane and the frictional force is directed down the plane as shown in Fig. 8.6.28 (b). Example 8.6.28 A 300 N force is required to pull the body resting on a horizontal plane. The force is inclined at an angle of 30° with horizontal. If the direction of the force is reversed to push the body, the force required is 350 N. Find the value of coefficient of friction and mass of the body. Solution : Refer Fig. 8.6.29 (a). Substituting the value of RN in equation (i) Substituting the value of RN in equation (iii) Subtracting equation (ii) from equation (iv) Now, substitute the value of μ in equation (ii), Example 8.6.29 An effort of 1500 N is required to just move a certain body up an inclined plane of angle 12, force acting parallel to the plane. If the angle of inclination is increased to 15°, then the effort required is 1720 N. Find the weight of the body and coefficient of friction. Solution : Examples for Practice Q.1 A body resting on a rough horizontal plane required a pull of 18 N inclined at 30° to the plane to just move it. It was found that a push of 22 N inclined at 30° to the plane just moved the body. Determine the weight of the body and coefficient of friction. [Ans. : W = 99 N, μ = 0.1732] Q.2 Determine the range of values of P for which the block of 500 N weight will be in equilibrium on an inclined plane shown in Fig. 8.6.31. Take μ = 0.35. [Ans.: 98.4 N ≤ P ≤ 401.55 N] Q.3 A block 'A' of weight 150 N rests on a block B of weight 250 N and tied with a string at D. (Take μAB = 0.2 and μBC = 0.3). Determine the pulling force P inclined at 30° and horizontal and applied to block B to start motion. Determine also tension in rope at D. (Refer Fig. 8.6.32). [Ans. : P = 113.87 N, T = 30 N] Q.4 A block weighing 20 kN is resting on a rough inclined plane as shown in Fig. 8.6.33. The block is tied with a horizontal string having a tension of 5 kN. Find i) The frictional force on- the block ii) Normal reaction of the inclined plane iii) The coefficient of friction between the surfaces of contact. [Ans.: Fr = 10.61 N, N1 = 17.68 N, μ = 0.6]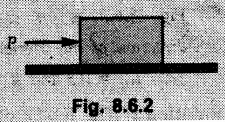





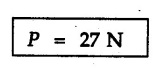












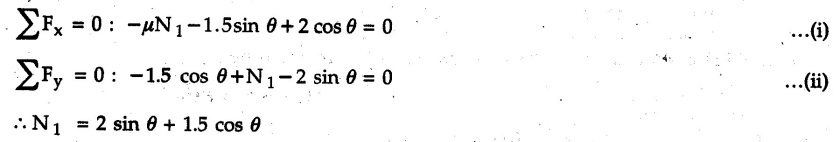
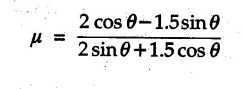


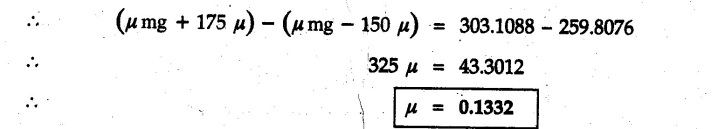


Engineering Mechanics: Unit IV: Friction : Tag: : - Solved Example & Practice Problems: Dry Friction
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
