Engineering Mechanics: Unit III: Distributed Forces
Solved Example & Practice Problems: Centre of Gravity, Centre of Mass and Centroid
Solved Example Problems, Examples for Practice: Centre of Gravity, Centre of Mass and Centroid - Distributed Forces - Engineering Mechanics
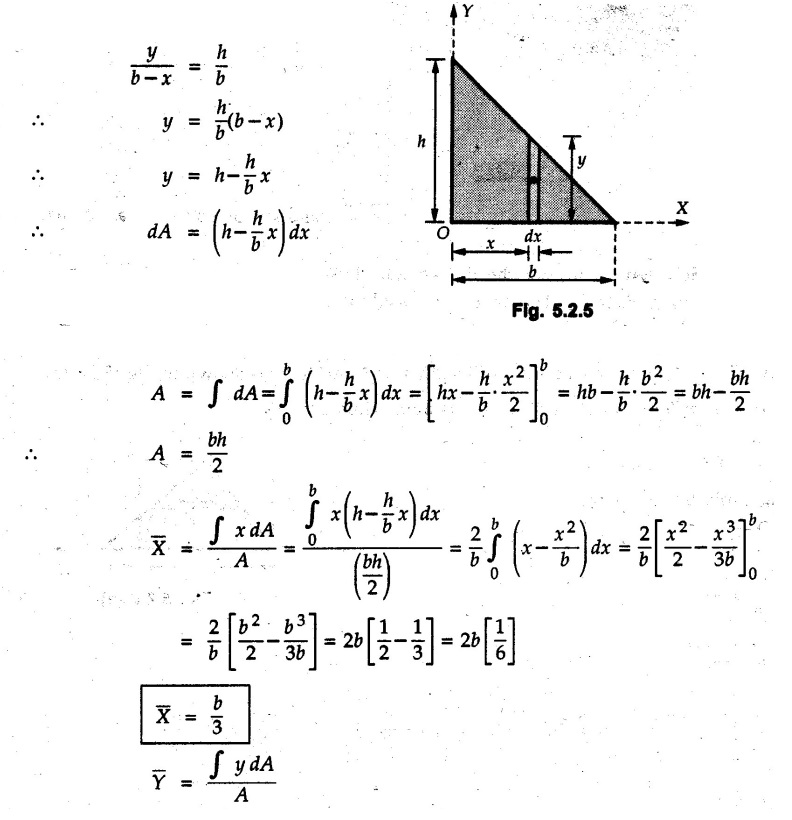
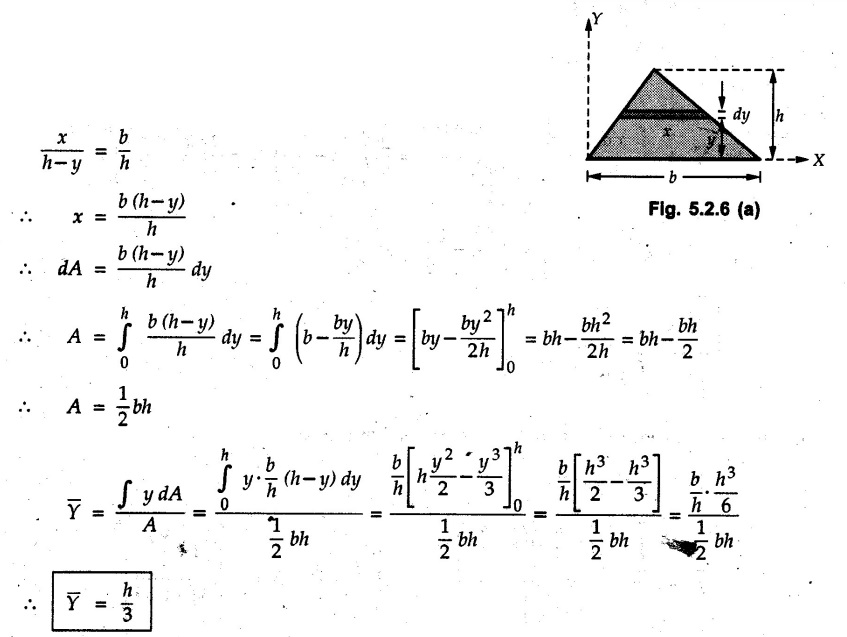
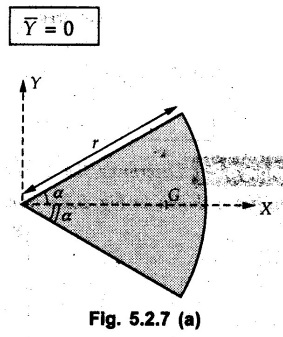
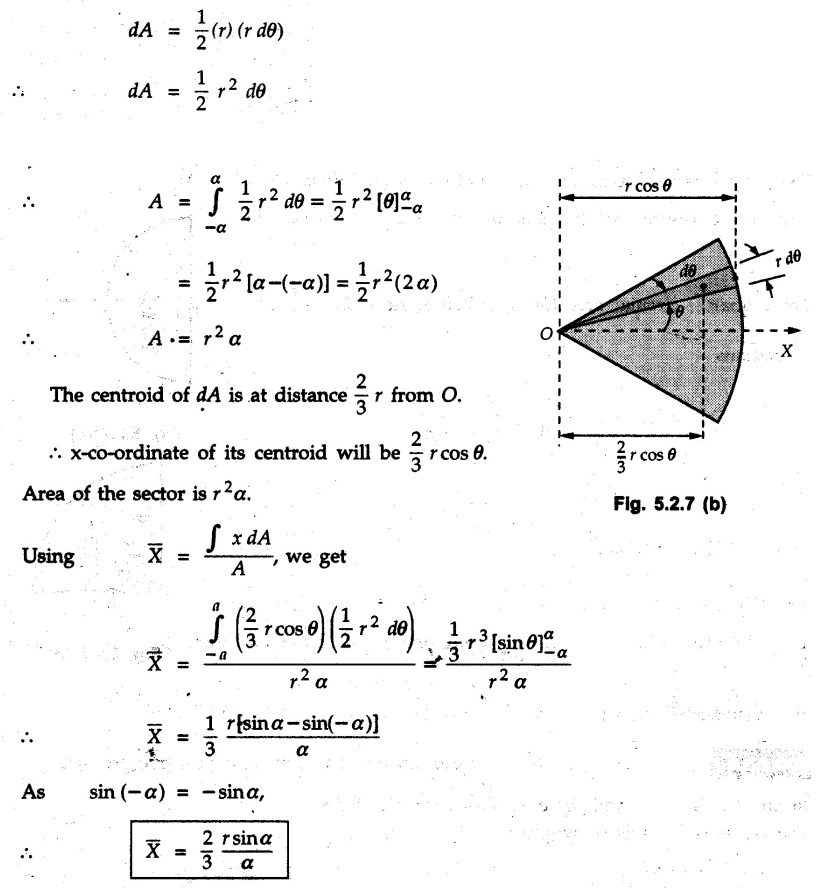
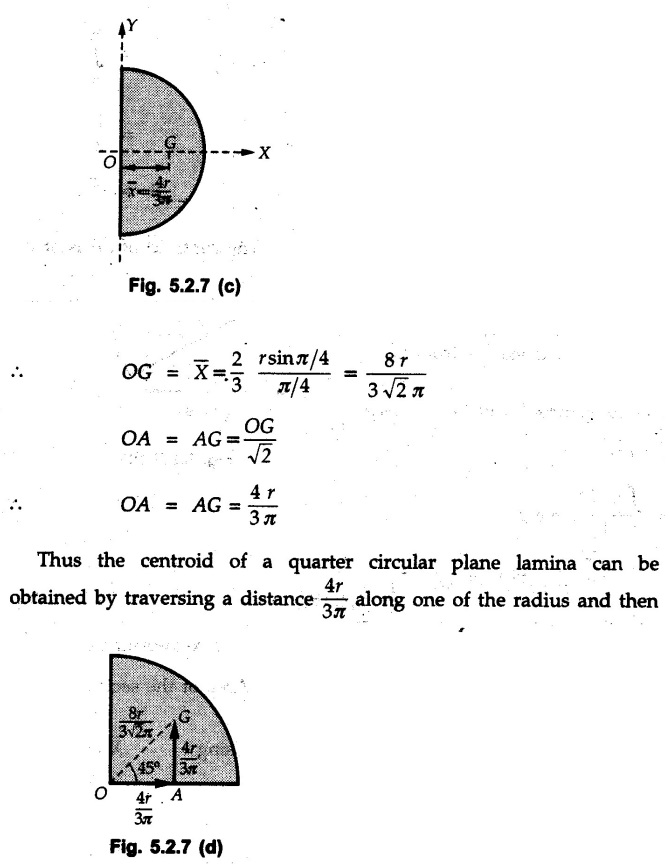
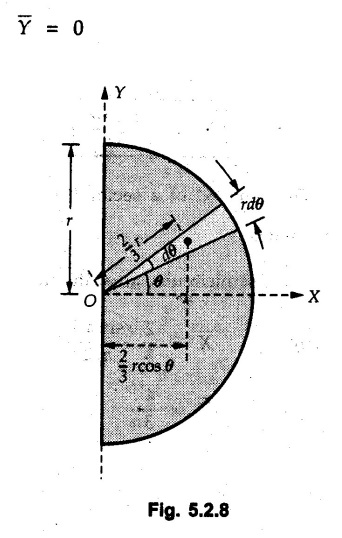
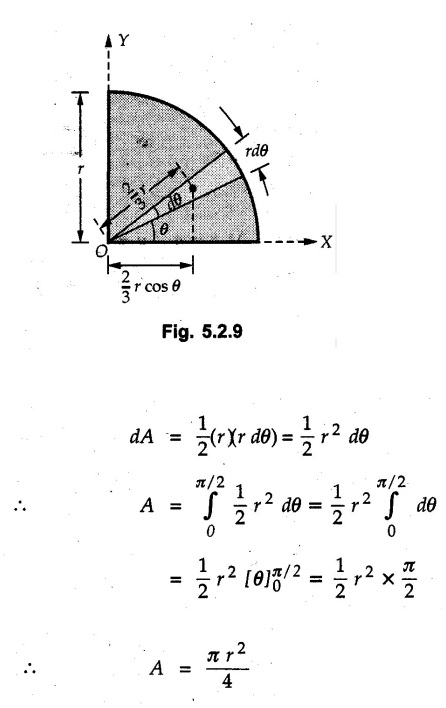
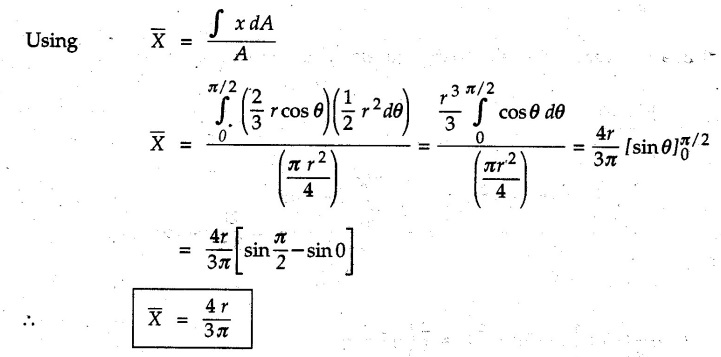
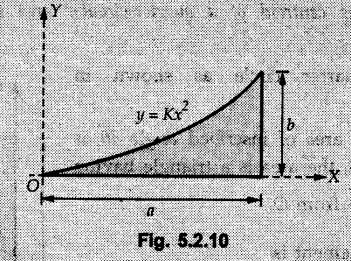
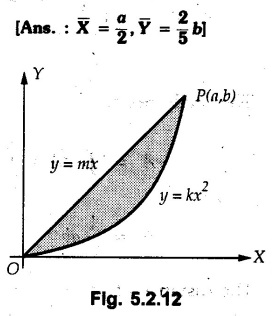
Solved Examples for Understanding Example 5.2.1 Determine the x and y co-ordinates of centroid of the rectangle shown in Fig. 5.2.4 from first principles. Solution : Consider the differential element to be a vertical strip of width dx as shown in Fig. 5.2.4 (a). The area of rectangle is A = a b The area of differential element is dA = b dx ⸫ A = ab The distance of centroid of differential element from Y-axis is x. The distance of centroid of differential element from X-axis is b/2. Example 5.2.2 Find the centroid of the area enclosed by a right angled triangle from first principles. Solution: Consider a right-angle triangle of base b and height h as shown in Fig. 5.2.5. Consider an elementary strip of width dx and height y parallel to Y-axis as shown.. As dx is very small, it is approximately a rectangular area. Its area is dA = y dx By similarity of triangles, where y is the centroidal distance of area dA from x-axis. Example 5.2.3 Determine the Y-co-ordinate of centroid of the triangular area of base b and height h shown in Fig. 5.2.6 from first principles. Solution : Consider a horizontal strip of length x and width dy as shown in Fig. 5.2.6 (a) The area of differential element which is approximately a rectangle, is dA = x dy Using similarity of triangles, Example 5.2.4 Obtain centroidal distance for a sector of angle 2a from first principles. Use it to locate centroid of semicircular and quarter circular plane laminae. Solution: Consider a sector as shown in Fig. 5.2.7 (a) with inscribed angle 2 α. Let the X-axis be the axis of symmetry. Then, Consider a triangular element as shown in Fig. 5.2.7 (b). The area of the triangular element will be The centroid of a sector lies on the line of symmetry at a distance of For a semicircular area, the inscribed angle is 2α = π, i.е., α = π/2 radians. Thus, for a semicircular area, the centroid is at a distance of 4r / 3π from the centre on the axis of symmetry as shown in Fig. 5.2.7 (c). For a quarter circular area the inscribed angle is 2α = π/2, i.e., α = π/4 radians Thus the centroid of a quarter circular plane lamina can be obtained by traversing a distance 4r / 3π along one of the radius and then again a distance 4r / 3π in a perpendicular direction as shown in Fig. 5.2.7 (d). Example 5.2.5 Determine the centroid of a semi-circular area of radius r from rst principles. Solution : Consider a semicircle as shown in Fig. 5.2.8. As the x-axis is the axis of symmetry. Consider an elementary area of inscribed angle dθ as shown in Fig. 5.2.8. As dθ is very small, the area is a triangle having its centroid at distance 2r /3 from O. The area of the triangular element is The x- co-ordinate of centroid of the triangular elementary area is 2/3 r cos θ. The centroid of a semicircle lies on the line of symmetry at a distance of 4r/3π from the centre. Example 5.2.6 Determine the centroid of a quarter-circular area of radius r from first principles. Solution: Consider a quarter circle as shown in Fig. 5.2.9. Consider an elementary area of inscribed angle de as shown. As de is very small, the area is a triangle having its centroid at a distance 2r/3 from O. The area of triangular element is The x- co-ordinate of centroid of the triangular elementary area is 2r/3 cos θ. The line of symmetry is a line making angle 45° with X-axis. This line divides the quarter circle into two equal areas. As centroid lies on this line of symmetry, Example 5.2.7 Determine co-ordinates of centroid of the shaded region shown in Fig. 5.2.10. Solution: At x = a, y = b ⸫ y = Kx2 ⇒ b = Ka2 ⸫ K = b/ a2 Consider the differential element to be a vertical strip of width dx and height y as shown in Fig. 5.2.10 (a). Area of differential element is dA = y dx The distance of centroid of differential element from Y-axis is x. The distance of centroid of differential element from X-axis is y/2. Examples for Practice Q.1 Prove that Q.2 Obtain centroidal distances from reference axes for the shaded area shown in Fig. 5.2.12.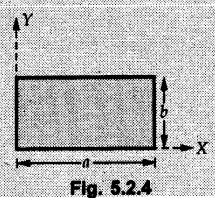
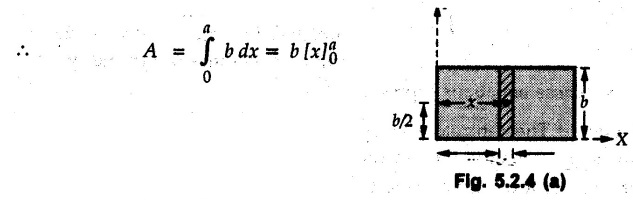
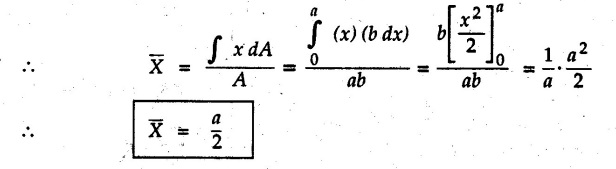
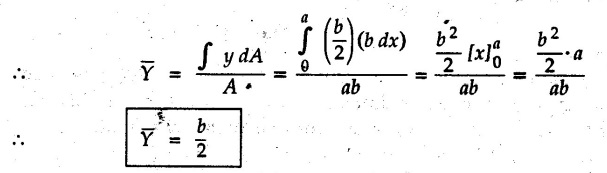
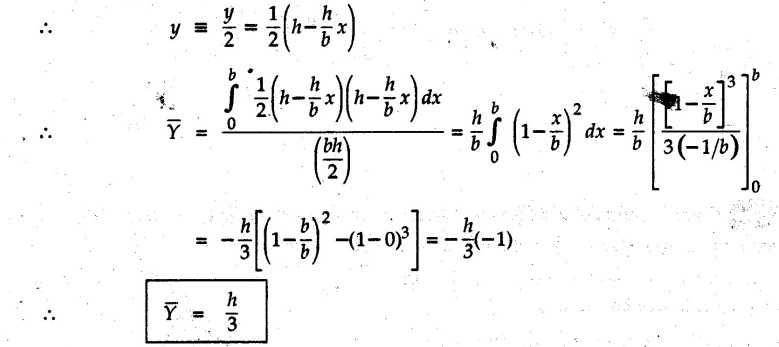
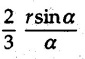 from the centre.
from the centre.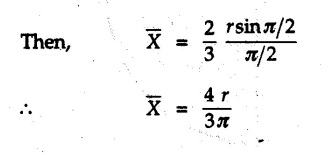
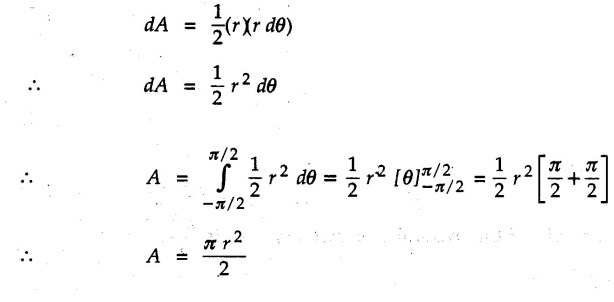
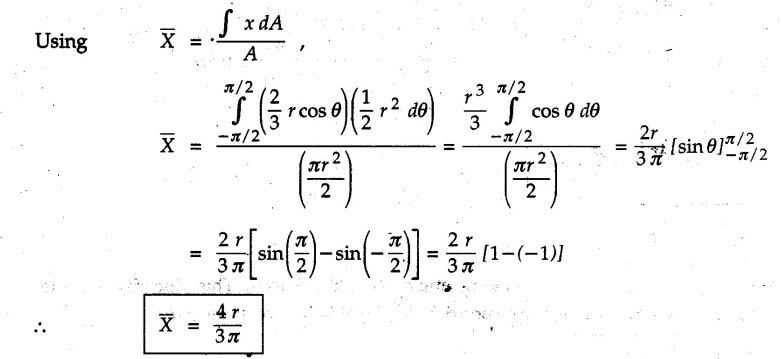
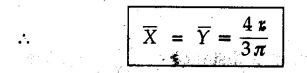
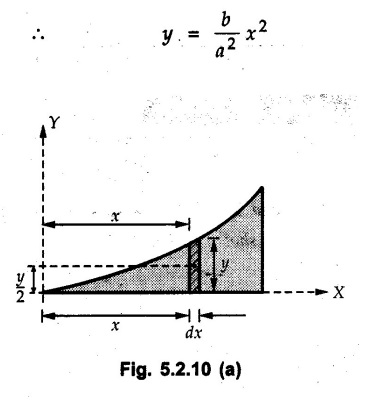
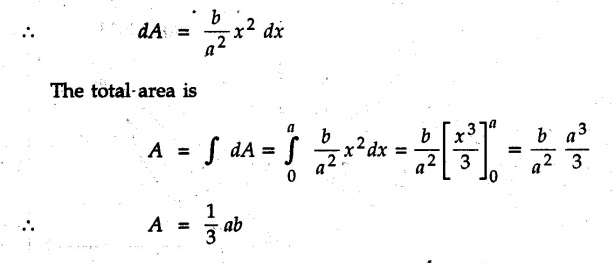
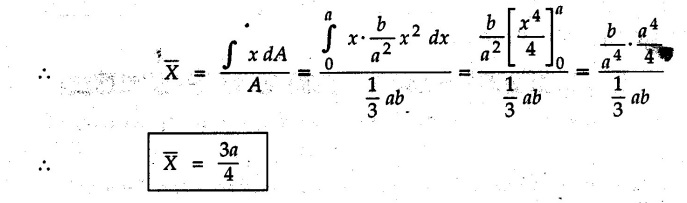
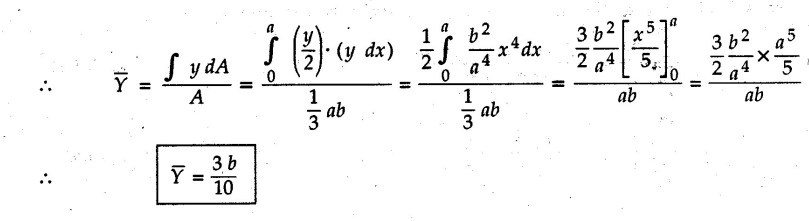
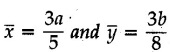 for the part of parabolic area bounded by X axis, line x = a and parabola y2 = kx as shown in Fig. 5.2.11.
for the part of parabolic area bounded by X axis, line x = a and parabola y2 = kx as shown in Fig. 5.2.11.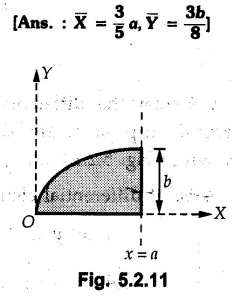
Engineering Mechanics: Unit III: Distributed Forces : Tag: : - Solved Example & Practice Problems: Centre of Gravity, Centre of Mass and Centroid
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
