Engineering Thermodynamics: Unit IV: Properties of Pure Substances
Solved Anna University Problems on Thermodynamic Processes
Solved Anna University Problems on Thermodynamic Processes: Properties of Pure Substances - Engineering Thermodynamics
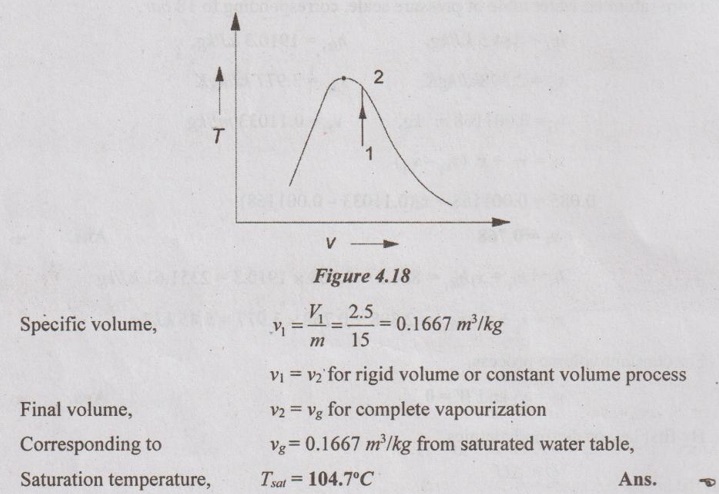
SOLVED ANNA UNIVERSITY PROBLEMS ON THERMODYNAMIC PROCESSES AU Problem 4.1 A vessel of volume 0.04 m3 contains a mixture of saturated water and steam at a temperature of 250°C. The mass of the liquid present is 9 kg. Find the pressure, mass, specific volume, enthalpy, entropy and internal energy. Given data: V = 0.04 m3 T = 250°C m1 = 9 kg To find: p, m, v, h, S and U Solution: From saturated water table of temperature scale, corresponding to 250°C, vf = v = 0.001251 m3/kg vg = vs = 0.050037 m3/kg AU Problem 4.2 A vessel with a capacity of 0.05 m3 contains a mixture of saturated water and saturated steam at a temperature of 245°C. The mass of the liquid present is 10 kg. Find the following: (1) Pressure (2) Mass (3) Specific volume (4) Specific enthalpy (5) Specific entropy and (6) Specific internal energy. Similar to AU Problem 4.1 on Page 4.60. [Ans:- Pressure, p = 36.5 bar, mass, m = 10.688 kg, specific volume, v = 0.004654 m3/kg, specific enthalpy, h = 1172.77 kJ/kg, specific entropy, s = 2.9623 kJ/kgK and specific internal energy, u = 1155.78 kJ/kg] AU Problem 4.3 A 0.5 m3 vessel contains 10 kg refrigerant 134a at -20°C. Determine the pressure, total internal energy and volume occupied by the liquid phase. Given data: V = 0.5 m3 m = 10 kg T1 = -20°C Solution: AU Problem 4.4 A rigid tank of 0.03 m3 capacity contains wet vapour at 80 kPa. If the wet vapour mass is 12 kg, calculate the heat added and quality of the mixture when the pressure inside the tank reaches 7 MPa. Given data: V1 = V2 = 0.03 m3 (⸪ rigid tank) p1 = 80 kPa = 0.8 bar m = 12 kg p2 = 7 MPa = 70 bar = 7000 kPa Solution: AU Problem 4.5 3 kg of steam at 18 bar occupies a volume of 0.2550 m3. During a constant volume process, the heat rejected is 1320 kJ. Determine the final internal energy and find initial dryness and work done. Given data: V1 = 0.255 m3 p1 = 18 bar = 1800 kPa m = 3 kg Heat rejected, Q = -1320 kJ Solution: AU Problem 4.6 A rigid tank with a volume of 2.5 m3 contains 15 kg of saturated liquid vapour mixture of water at 75°C. Now the water is slowly heated. Determine the temperature at which the liquid in the tank is completely vapourized. Also, show the processes on T-v diagram with respect to saturation lines. Given data: V1 = V2 = 2.5 m3 ( ⸪ rigid tank) m = 15 kg T1 = 75°C Solution: AU Problem 4.7 Steam initially at 0.3 MPa, 250°C is cooled at constant volume. At what temperature will the steam become saturated vapour? What is the steam quality at 80°C. Also find what is the heat transferred per kg of steam in cooling from 250°C to 80°C. Given data: p1 = 0.3 MPa = 3 bar = 300 kPa T1 = 250°C T2 = 80°C Process: Constant volume To find: T2', x2 and Q Solution: From saturated water table of pressure scale, corresponding to 3 bar, Tsat = 133.5°C Since T1 > Tsat, the state would be in the superheated region. From superheated enthalpy and superheated specific volume tables, at 3 bar and 250°C v1 = 0.7964 m3/kg h1 = 2967.9 kJ/kg Let v2' be the specific volume of steam at saturated vapour condition, Since steam is cooled at constant volume, v1 = v2' = v2 = 0.7964 m3/kg If the steam becomes saturated vapour, v2' = vg2 = 0.7964 m3/kg Corresponding to vg2 = 0.7964 m3/kg, from saturated water table, the saturation temperature can be noted down. We know that h2 = hf2 + x2hfg2 = 334.9 + 0.2334 × 2308.9 = 873.8 kJ/kg According to first law of thermodynamics, Work, W = Q + ΔU Heat transfer, Q = -ΔU Since, W = 0 for constant volume process = m (u1 - u2) But, h = u + pv Heat transfer, Q = (h2 - p2v2) - (h1 – p1v1) = (h2 - h1) - (p2v2 - p1v1) = (h2 - h1) - v1 (p2 - p1) [⸪ v1 = v2] = (873.8 - 2967.9) - 0.7964 (47.36 - 300) = -1892.89 kJ/kg Ans. AU Problem 4.8 A pressure cooker contains 1.5 kg of saturated steam at 5 bar. Find the quantity of heat which must be rejected so as to reduce the quality to 60% dry. Determine the pressure and temperature of the steam at the new state. Given data: m = 1.5 kg' p1 = 5 bar = 500 kN/m2 x1 = 1 x2 = 0.6 Solution: From saturated water table of pressure scale at 5 bar, Ts = 151.8°C = 151.8 + 273 = 424.8 K h1 = hg1 = 2747.5 kJ/kg v1 = vg1 = 0.37466 m3/kg Internal energy of steam per kg at initial state 1, u1 = h1 – p1v1 = 2747.5 - (500 × 0.37466) = 2560.2 kJ/kg Volume of pressure cooker, V1 = m v1 = 1.5 × 0.37466 = 0.562 m3 Since pressure cooker has constant volume, V1 = V2. AU Problem 4.9 Ten kg of water of 45°C is heated at a constant pressure of 10 bar until it becomes superheated vapour at 300°C. Find the change in volume, change in enthalpy, change in internal energy and change in entropy. Given data: m = 10 kg T1 = 45°C Process: Constant volume ⸫ p1 = p2 = 10 bar = 1000 kPa T2 = 300°C To find: ΔV, Δh, ΔS and ΔU Solution: From saturated water table of temperature scale, corresponding to 45°C, v1 = vf1= 0.001010 m3/kg, h1 = hf1 = 188.4 kJ/kg, s1 = sf1 = 0.638 kJ/kg K From saturated water table of pressure scale, corresponding to 10 bar, Tsat = 179.9°C Since T2 > Tsat, the state would be in the superheated region. From superheated enthalpy, superheated entropy and superheated specific volume tables, corresponding to 10 bar and 300°C, h2 = 3052.1 kJ/kg, s2 = 7.125 kJ/kg K, v2 = 0.258 m3/kg AU Problem 4.10 A steam boiler initially contains 5 m3 of steam and 5 m3 of water at 1 MPa. Steam is taken out at constant pressure until 4 m3 of water is left. What is the heat transferred during the process? Given data: Vs1 = 5 m3 Vw1 = 5 m3 p = 1 MPa = 10 bar = 1000 kPa Process: Constant volume Vw2 = 4 m3 Solution: From saturated water table of pressure scale, corresponding to 10 bar, Initial energy stored in saturated water and steam + Heat transferred from the external source = Final energy stored in saturated water and steam + Energy leaving with steam. U1 + Q = U2 + ms hg m1hf + m1shfg + Q = m2hf + m2shfg + mhg (⸪ ms = m) 4462.29 × 761.68 + 25.73 × 2583.6 + Q = 3580.13 × 761.68 + 30.86 × 2583.6 + 882.16 × 2778.1 Q = 1792058.9 kJ = 1792.06 MJ Ans. AU Problem 4.11 Steam initially at 1.5 MPa, 300°C expands reversibly and adiabatically in a steam turbine to 40°C. Determine the ideal work output of the turbine per kg of steam. Given data: p1 = 1.5 MPa = 15 bar T1 = 300°C T2 = 40°C To find: W Solution: From saturated water table of pressure scale, corresponding to 15 bar, Tsat = 198.3°C Since T1 > Tsat, the state would be in the superheated region. From superheated enthalpy and superheated entropy tables, corresponding to 15 bar and 300°C, h1 = 3038.9 kJ/kg s1 = 6.921 kJ/kgK From saturated water table of pressure scale, corresponding to 40°C, hf2 = 167.5 kJ/kg, sf2 = 0.572 kJ/kgK, sg2 = 8.258 kJ/kg K hfg2 = 2406.9 kJ/kg, sfg2 = 7.686 kJ/kgK, We know that for reversible adiabatic process, s2 = s1 = 6.921 kJ/kgK Since s2 < sg2, the steam in wet condition after expansion in the turbine. But s2 = sf2 + x2 sfg2 6.921 = 0.572 + x2 × 7.686 x2 = 0.826 ⸫ Enthalpy at exit, h2 = hf2 + x2 hfg2 = 167.5 + 0.826 × 2406.9 = 2155.6 kJ/kg Work output of turbine, WT = h1 - h2 = 3038.9 - 2155.6 = 883.3 kJ/kg Ans. AU Problem 4.12 Steam at 30 bar and 350°C is expanded in a non flow isothermal process to a pressure of 1 bar. The temperature and pressure of the surroundings are 25°C and 100 kPa respectively. Determine the maximum work that can be obtained from this process per kg of steam. Also find the maximum useful work. Given data: p1 = 30 bar = 3000 kPa T1 = 350°C p2 = 1 bar = 100 kPa po = 100 kPa To = 25°C = 273 + 25 = 298K To find: Wmax and (Wu)max Solution: From saturated water table of pressure scale, corresponding to 30 bar, Tsat = 233.8°C Since T1 > Tsat, the state would be in the superheated region. From superheated enthalpy, superheated entropy and superheated specific volume tables, corresponding to 30 bar and 350°C, s1 = 6.747 kJ/kgK h1 = 3117.5 kJ/kg v1 = 0.09053 m3/kg pv = C for non-flow isothermal (hyperbolic) process p1v1 = p2v2 AU Problem 4.13 1 kg of steam initially dry saturated at 1.1 MPa expands in a cylinder following the law pV1.13 = C. The pressure at the end of expansion is 0.1 MPa. Determine the: (i) final volume (ii) final dryness fraction (iii) Work done (iv) change in internal energy (v) heat transferred. Given data: m = 1 kg p1 = 1.1 MPa = 11 bar = 1100 kPa p2 = 0.1 MPa = 1 bar рv1.13 = C Solution: From saturated water table of pressure scale, at 11 bar, v1 = vg1 = 0.17739 m3/kg h1 = hg1 = 2779.7 kJ/kg From polytropic relation, p1v11.13 = p2v21.13 AU Problem 4.14 Steam at a pressure of 15 bar and 250°C expands according to the law pv1.25 = C to a pressure of 1.5 bar. Evaluate the final conditions, work done, heat transfer and change in entropy. The mass of the system is 0.8 kg. Given data: p1 = 15 bar = 1500 kPa T1 = 250°0 pvl.25 = C p2 = 1.5 bar = 150 kPa m = 0.8 kg Solution: From saturated water table of pressure scale, corresponding to 15 bar, Tsat = 198.3°C Since T1 > Tsat, the state would be in the superheated region. From superheated enthalpy, superheated entropy and superheated specific volume tables, corresponding to p1 = 15 bar and T1 = 250°C, v1 = 0.152 m3/kg h1 = 2923.5 kJ/kg s1 = 6.71 kJ/kgK According to the law, pvl.25 = C p1v11.25 = p2v21.25 AU Problem 4.15 In a steam generator, compressed water at 10 MPa, 30°C enters a 30 mm diameter tube at the rate of 3 litres/s. Steam at 9 MPa and 400°C exit the tube. Find the rate of heat transfer. Given data: p1 = 10 MPa = 100 bar = 10000 kPa Tw = 30°C D = 30 mm = 0.03 m v1 = 3 litres/s = 0.003 m3/s p2 = 9 MPa = 90 bar = 9000 kPa T2 = 400°C To find: Q Solution: From saturated water table of temperature scale, corresponding to 30°C, AU Problem 4.16 Steam flows through a small turbine at the rate of 500 kg/h entering at 15 bar, 300°C and leaving gat 0.1 bar with 4% moisture. The steam enters at 80 m/s at a point 2 m above the discharge and leaves at 40 m/s. Compute the shaft power assuming that the device is adiabatic but considering kinetic and potential energy changes. Calculate the areas of the inlet and discharge tubes. Given data: m = 500 kg/hr =500/3600 = 0.139 kg/s p1 = 15 bar = 1500 kPa T1 = 300°C p2 = 0.1 bar = 10 kPa x2 = 100 - 4 = 96% = 0.96 C1 = 80 m/s C2 = 40 m/s z1 - z2 = 2 m Solution: From superheated enthalpy and superheated entropy tables, at 15 bar and 500°C, h1 = 3038.9 kJ/kg v1 = 0.1679 m3/kg From saturated water table of pressure scale, corresponding to 0.1 bar, AU Problem 4.17 The power output of an adiabatic steam turbine is 5 MW, and the state of steam entering the turbine is: pressure 2 MPa; temperature 400°C; velocity 50 m/s; elevation 10 m. The state of the steam leaving the turbine is: pressure 15 kPa; dryness fraction 0.9; velocity 180 m/s; elevation 6 m. Determine the (i) change in enthalpy, kinetic energy and potential energy. (ii) work done per unit mass of the steam flowing through the turbine. (iii) mass flow rate of the steam. Given data: P = 5 MW = 5000 kW p1 = 2 MPa = 20 bar T1 = 400°C = 400 + 273 = 673 K C1 = 50 m/s z1 = 10 m p2 = 15 kPa = 0.15 bar Dryness fraction, x2 = 0.9 C2 = 180 m/s z2 = 6m Q = -0.29 kJ/s (⸪ Heat loss) m = 0.42 kg/s Solution: For this AU problem 4.17, we need to use "Steam Tables" as pressure and temperature are given at inlet and exit of steam turbines. From saturated water table of pressure scale, corresponding to p1 = 20 bar, the saturation temperature is 212.4°C. But the given temperature is 400°C. Therefore, the given steam is in superheated condition. From superheated enthalpy table, at 20 bar and 400°C, the enthalphy h1 = 3248.7 kJ/kg From saturated water table of pressure scale, corresponding to p2 = 0.15 bar, AU Problem 4.18 Steam at 0.8 MPa, 250°C and flowing at the rate of 1 kg/s passes into a pipe carrying wet steam at 0.8 MPa, 0.95 dry. After adiabatic mixing the flow rate is 2.3 kg/s. Determine the properties of the steam after mixing. Given data: p1 = 0.8 MPa = 8 bar = 800 kPa T1 = 250°C m1 = 1 kg/s p2 = 0.8 MPa = 8 bar = 800 kPa x2 = 0.95 m3 = 2.3 kg/s To find: Properties Solution: Sum of mass of the steam before mixing = Sum of mass of the steam after mixing m1 + m2 = m3 m2 = m3 - m1 = 2.3 – 1 = 1.3 kg/s The energy balance equation for adiabatic mixing, m1h1 + m2h2 = m3h3 ... (4.2) From saturated water table of pressure scale, corresponding to 8 bar, Tsat = 171.4°C Since T1 > Tsat, the state would be in the superheated region. From superheated enthalpy table, corresponding to 8 bar and 250°C, h1 = 2950.4 kJ/kg From saturated water table of pressure scale, corresponding to 8 bar, hf2 = 720.9 kJ/kg, hfg2 = 2046.5 kJ/kg, ⸫ h2 = hf2 + x2 hfg2 = 720.9 + 0.95 × 2046.5 = 2665.08 kJ/kg Substituting all the values to the equation (4.2), 1 × 2950.4 + 1.3 × 2665.08 = 2.3 × h3 h3 = 2789.13 kJ/kg From saturated water table of pressure scale, corresponding to 8 bar, hg = 2767.4 kJ/kg Since h3 > hg, the steam is in superheated condition. From the Mollier chart, corresponding to 8 bar and h3 = 2789.13 kJ/kg, Superheated temperature, T3 = 180°C Ans. Entropy, s3 = 6.645 kJ/kg K Ans. Specific volume, v3 = 2.5 m3/kg Ans. AU Problem 4.19 Two streams of steam, one at 2 MPa, 300°C and the other at 2 MPa, 400°C, mix in a steady flow adiabatic process. The rates of flow of the two streams are 3 kg/min and 2kg/min respectively. Evaluate the final temperature of the emerging steam if there is no pressure drop due to the mixing process. What would be the rate of increase in the entropy of the universe? This steam with negligible velocity now expands adiabatically in a nozzle to a pressure of 1 kPa. Determine the exit velocity of the stream and exit area of the nozzle. Given data: p1 = 2 MPa = 20 bar = 2000 kPa T1 = 300°C p2 = 2 MPa = 20 bar = 2000 kPa T2 = 400°C m1 = 3 kg/min m2 = 2 kg/min p3 = 2 MPa = 20 bar = 2000 kPa m3 = m1 + m2 = 3 + 2 = 5 kg/min = m4 p4 = 1 kPa = 0.01 bar Solution: From saturated water table of pressure scale, corresponding to 20 bar, Tsat 212.4°C Since T1 > Tsat, the state would be in the superheated region. Corresponding to 20 bar at 300°C from superheated enthalpy, superheated entropy and superheated specific volume tables, h1 = 3025 kJ/kg s1 = 6.77 kJ/kgK Similarly, corresponding to 20 bar at 400°C, from superheated enthalpy and superheated entropy tables, h2 = 3248.7 kJ/kg s2 = 7.13 kJ/kgK From superheated enthalpy table, corresponding to h3 = 3114.48 kJ/kg at 20 bar, the superheated temperature, T3 = 339.38°C Ans. Similarly, entropy after mixing, AU Problem 4.20 A large insulated vessel is divided into two chambers, one containing 5 kg of dry saturated steam at 0.2 MPa and the other 10 kg of steam, 0.8 quality at 0.5 MPa. If the partition between the chambers is removed and the steam is mixed thoroughly and allowed to settle, find the final pressure, steam quality and entropy change in the process. Given data: m1 = 5 kg p1 = 0.2 MPa = 2 bar = 200 kPa m2 = 10 kg x2 = 0.8 p2 = 0.5 MPa = 5 bar = 500 kPa Solution: Mass of steam after mixing, m3 = m1 + m2 = 5 + 10 = 15 kg Specific volume of wet steam, v2 = v2 + x2 vƒg2 v2 = vƒ2 + x2 (vg2 - vƒ2) = 0.001093 + 0.8 (0.37466 - 0.001093) = 0.3 m3/kg AU Problem 4.21 In a power station, the saturated steam is generated at 200°C by transferring the heat from hot gases in a steam boiler. The gases are cooled from 1000°C to 500°C and all the heat from gases goes to water. Assume water enters the boiler at saturated condition and leaves as saturated steam. Calculate the mass of gas required to produce a kg of steam and ii) Find the increase in total entropy of the combined system of gas and water and increase in unavailable energy due to irreversible heat transfer. Take Cp (for gas) = 1.0 kJ/kgK, hfg (latent heat of steam at 200°C) = 1940.7 kJ/kg. Given data: Temperature of steam, Ts = 200°C = 200 + 273 = 473 K Initial temperature of gases, T1g = 1000°C = 1000 + 273 = 1273 K Final temperature of gases, T2g = 500°C = 500 + 273 = 773 K For gases, Cpg = 1.0 kJ/kg K Latent heat of steam at 200°C, hfg =1940.7 kJ/kg Solution:

















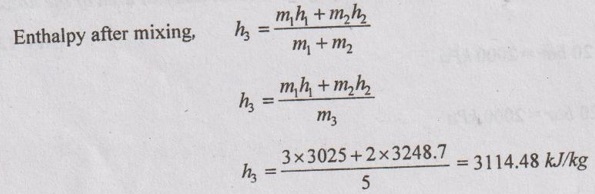


 Entropy of wet steam, s2 = sf2 + x2 sfg2 = 1.86 + 0.8 × 4.959 = 5.83 kJ/kgK
Entropy of wet steam, s2 = sf2 + x2 sfg2 = 1.86 + 0.8 × 4.959 = 5.83 kJ/kgK

Engineering Thermodynamics: Unit IV: Properties of Pure Substances : Tag: : - Solved Anna University Problems on Thermodynamic Processes
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
