Basic Electrical and Electronics Engineering: Unit I: Electrical Circuits
Series and Parallel Combinations of Resistances
with Solved Example Problems
A set of resistances are connected in series if the same current flows through them and there is only one path for the current flow throughout.
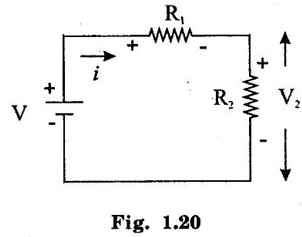
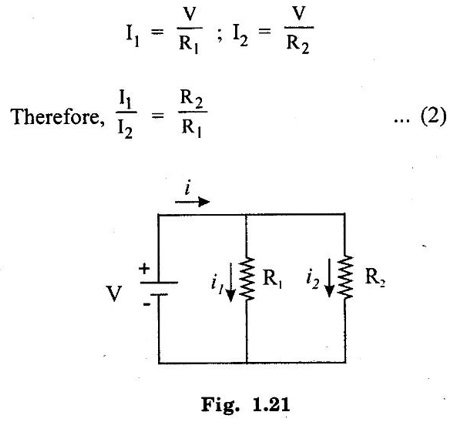
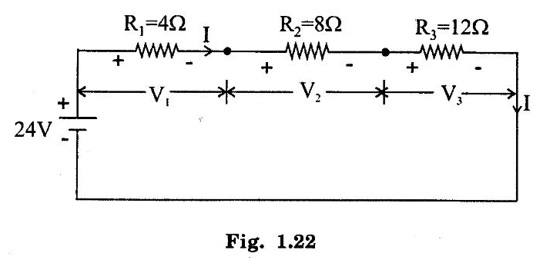
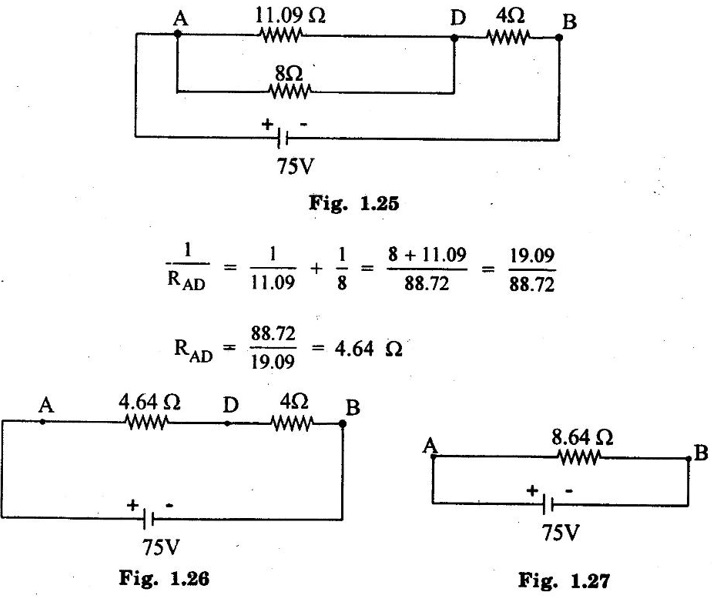
SERIES AND PARALLEL COMBINATIONS OF RESISTANCES A set of resistances are connected in series if the same current flows through them and there is only one path for the current flow throughout. It is illustrated in figure 1.18. Consider n-resistances R1, R2, R3 ... Rn connected in series across a battery V volts. Then the total resistance is given by, Req = R1 + R2 + R3... + Rn The above circuit being a series circuit, it is to be noted that, (i) same current flows through all the resistors (ii) voltage drop across each is different due to its resistance being different (iii) sum of the all voltage drops is equal to the voltage supplied the battery (i.e.,) V = V1 + V2 + V3 +... Vn = I R1 + IR2 + IR3 +... + IRn (since ohms law) A set of resistances are in parallel when the source voltage is applied across each resistor is the same and there are many paths for current as the number of resistors. It is illustrated in figure 1.19. Consider n resistances are connected in parallel across a battery V volts. Then the total resistance is given by In this case (i) Potential difference across all resistance is same (ii) Current in each resistor is different (iii) The total current is sum of three separate branch currents. This rule is used for finding voltage drop across different resistors connected in series. Since in a series circuit, same current flows through each resistor, voltage drop varies directly with its resistance. Figure 1.20 shows a voltage source connected across a series combination of two resistors. Figure 1.21 shows two resistances R1 and R2 connected in parallel across a voltage V. According to ohms law, the current in each branch is given by The division of current in the branches of a parallel circuit is inversely proportional to their resistances. We can express the branch current interms of the total circuit current as follows: Problem 1.3 Three resistors are connected in series with 12 V battery, find the voltage across the three resistors 4Ω, 8Ω and 12Ω of circuit shown in figure 1.22. Solution : Total resistance = R = R1 + R2 + R3 = 4 + 8 + 12 = 24 Ω According to voltage division rule, voltage drop across three resistors, Problem 1.4 In the figure 1.23 is shown a combination resistances. If the voltage across A and B is 75 Volts. Determine (i) The equivalent resistance of the circuit (ii) Voltage drop across each resistance. Solution: (i) Equivalent resistance of the circuit Resistance between A and C, Resistance of ACD Resistance between A and D Equivalent resistance of the circuit Voltage drop across 8Ω resistor = 5.04 × 8 = 40.32 V Voltage drop across 4Ω resistor = 8.68 × 4 = 34.72 V. Problem 1.5 A 60W, 200V lamp is connected in series with 40W, 240V lamp across 250 V supply. Determine (i) current taken (ii) voltage across each lamp and (iii) power given by the lamps. Assume that resistance of the lamps remain constant. Solution : When both lamps are in series, total resistance is the sum, Rtotal = 667 + 1440 = 2107 Ω. (ii) Voltage across 60W lamp = 0.118 × 667 = 78.706 V Voltage across 40W lamp = 0.118 × 1440 = 169.92 V (iii) Power (lamp 1) = 0.118 × 78.706 = 9.28 W Power (lamp 2) = 0.118 × 169.92 = 20.05 W1. Resistance in Series

2. Resistance in parallel


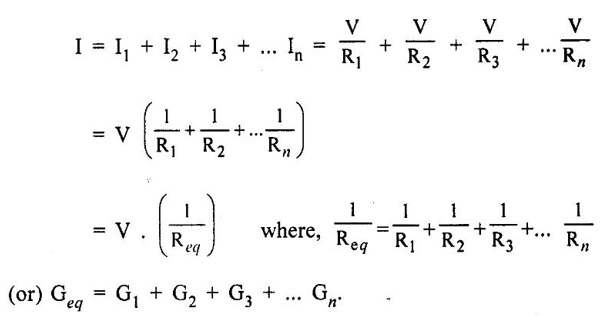
3. Voltage division rule
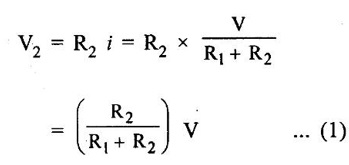
4. Current Division Rule

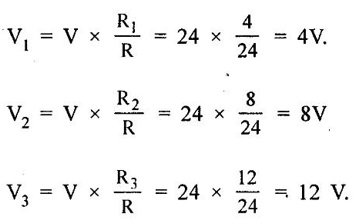

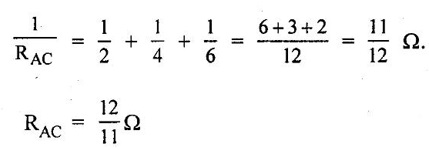

 Voltage drop across 10Ω resistor = 3.63 × 10 = 36.3 V
Voltage drop across 10Ω resistor = 3.63 × 10 = 36.3 V
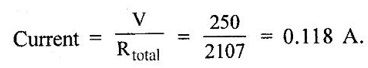
Basic Electrical and Electronics Engineering: Unit I: Electrical Circuits : Tag: : with Solved Example Problems - Series and Parallel Combinations of Resistances
Related Topics
Related Subjects
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation

