Engineering Graphics: Unit I (a): Geometrical Construction
Review of Simple Geometrical Constructions
Engineering Graphics (EG)
Bisector is a line which divides a line into two equal parts ie., AO = OB = 1/2 × AB. Hence Bisector is passing through the mid point of the line.
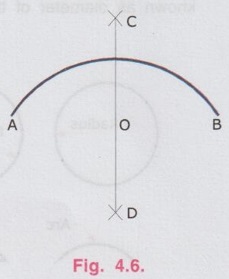
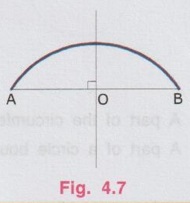
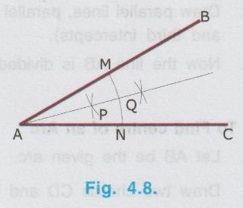
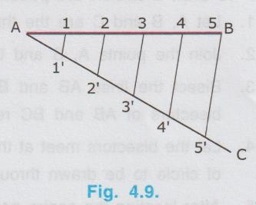
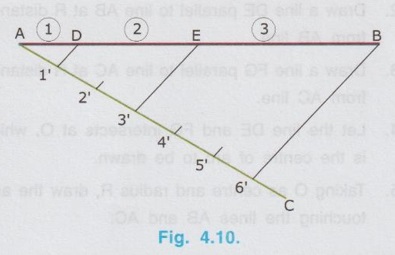
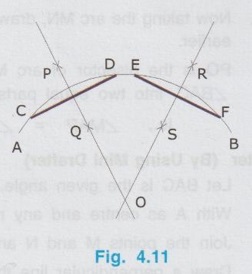
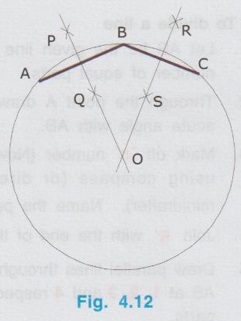
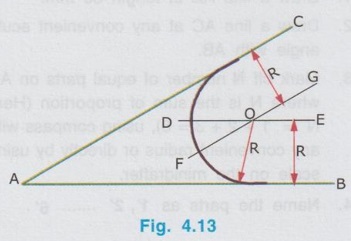
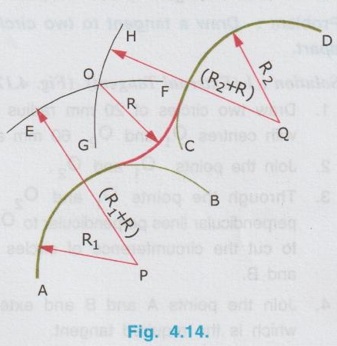
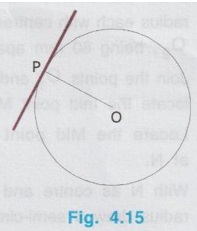
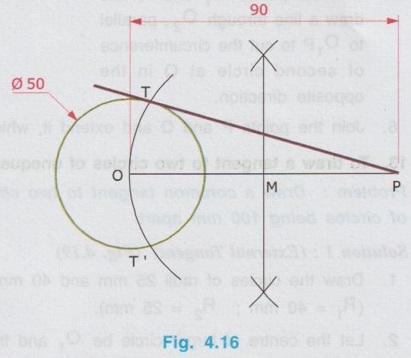
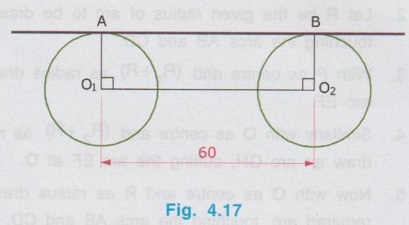
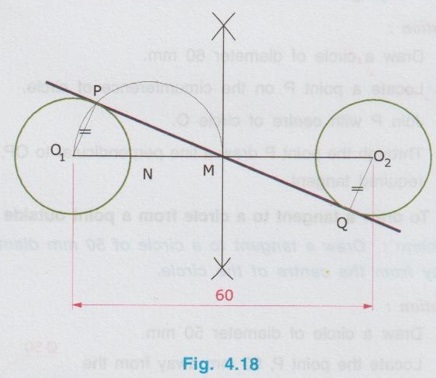
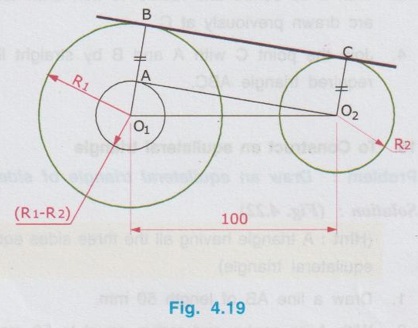
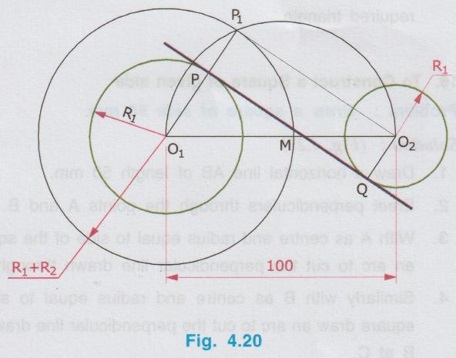
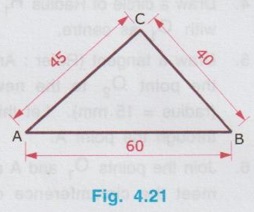
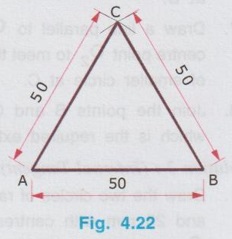
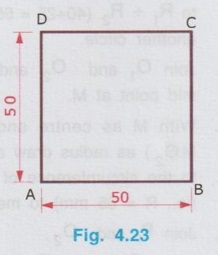
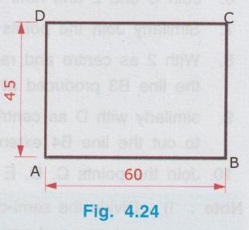
REVIEW OF SIMPLE GEOMETRICAL CONSTRUCTIONS 1. To bisect a straight line 1. Let AB be the given line. 2. Taking the end A as centre and radius more than half of the length of line AB, draw an arc above and below the line. 3. Similarly by taking B as centre and same radius draw arcs above and below the line to intersect the arc drawn in the previous step. 4. Let the arcs intersects at C and D. 5. Join the points C and D which is the required bisector of the line AB, bisect the line AB at O. Bisector is a line which divides a line into two equal parts ie., AO = OB = 1/2 × AB. Hence Bisector is passing through the mid point of the line. Bisector CD is perpendicular to the line AB. Hence, to draw a bisector using Minidrafter locate the mid popint of a line and draw a perpendicular line through the mid point. 2. To bisect an Arc : 1. Let AB be the given arc. 2. With A as centre and radius more than half of the length AB, draw arcs above and below the arc AB. 3. With B as centre and same radius cut the arcs drawn in the previous step. 4. Let the intersecting points be C and D. 5. Join the points C and D, which is the required bisector. Bisector of an arc is a straight line which divides the arc into two equal parts. Aliter (By Using Mini Drafter) 1. Let AB be the given arc. 2. Join the extremites of arc A and B, by a straight line. 3. Locate the midpoint of line AB and draw a perpendicular line through the mid point, which bisects the arc AB. 3. To bisect an angle 1. Let ∠BAC is the given angle. 2. Taking the point A as centre and any radius draw an arc MN. 3. Now taking the arc MN, draw its bisector PQ as explained earlier. PQ is the bisector of arc MN, which divides the angle ∠BAC into two equal parts. ie., ∠MAP = ∠PAN Aliter (By Using Mini Drafter) 1. Let BAC is the given angle. 2. With A as centre and any radius draw an arc MN. 3. Join the points M and N and locate its mid point. 4. Draw a perpendicular line through the mid point. 4. To divide a line 1. Let AB be the given line to be divided into 'n' (say 5) number of equal parts. 2. Through the point A draw a line AC at any convenient acute angle with AB. 3. Mark off `n' number (Now 5 parts) of parts on the AC using compass (or directly by using scale on the minidrafter). Name the parts as 1', 2', 3', 4' and 5'. 4. Join 5' with the end of the line, B. 5. Draw parallel lines throught the points 1', 2', 3' and 4', parallel to 5' B to cut the given line AB at 1, 2, 3 and 4 respectively. Now the line AB is divided into n (here 5) number of equal parts. 5. To divide a line in Proportional parts : Problem : Divide a line AB of length 80 mm into three parts in the ratio of 1:2: 3. Solution : 1. Draw a line AB of length 80 mm. 2. Draw a line AC at any convenient acute angle with AB. 3. Mark off N number of equal parts on AC where N is the sum of proportion (Here N = 1 + 2 + 3 = 6), using compass with any convenient radius or directly by using scale on the minidrafter. 4. Name the parts as 1', 2' ....... 6'. 5. Join the end intercept 6' with B. 6. Draw parallel lines, parallel to 6' B, passing through the required intercepts (Here through first and third intercepts). 7. Now the line AB is divided in the ratio 1:2:3 ie., AD : DE : EB = 1 : 2 : 3. 6. To Find centre of an Arc 1. Let AB be the given arc. 2. Draw two chords CD and EF of arbitrary lengths on the arc AB. 3. Draw the perpendicular bisectors PQ and RS for the chords CD and EF respectively. 4. Let the bisectors meet at O which is the required centre of an arc. 7. To draw a circle / arc passing through three points 1. Let A, B and C are the three given points. 2. Join the points A, B and C by straight lines. 3. Bisect the lines AB and BC. Let PQ and RS are the bisectors of AB and BC respectively. 4. Let the bisectors meet at the point O, which is the centre of circle to be drawn through the given points. 5. After locating the centre point o, arc (or) a circle may be drawn through the given points by taking OA (or OB or OC) as radius. 8. To draw an arc of given radius between two inclined lines 1. Let AB and AC be the inclined lines at an acute angle and 'R' be the radius of arc to be drawn in between these lines. 2. Draw a line DE parallel to line AB at R distance from AB line. 3. Draw a line FG parallel to line AC at R distance from AC line. 4. Let the line DE and FG intersects at O, which is the centre of arc to be drawn. 5. Taking O as centre and radius R, draw the arc, touching the lines AB and AC. 9. To draw an arc of given radius touching two given arcs 1. Let the arcs AB and CD are given with radius R1 and R2 at centres P and Q respectively. 2. Let R be the given radius of arc to be drawn by touching the arcs AB and CD. 3. With P as centre and (R1 + R) as radius draw an arc EF. 4. Similarly with Q as centre and (R2 + R) as radius draw an arc GH, cutting the arc EF at O. 5. Now with O as centre and R as radius draw the required arc, touching the arcs AB and CD. 10. To draw a tangent to a circle from a point on it Problem: Draw a tangent to a circle of 60 mm diameter through point P, lying on the circumference of the circle. Solution : 1. Draw a circle of diameter 60 mm. 2. Locate a point P on the circumference of circle. 3. Join P with centre of circle O. 4. Through the point P draw a line perpendicular to OP, which is the required tangent. 11. To draw a tangent to a circle from a point outside it. Problem : Draw a tangent to a circle of 50 mm diameter through point P, located at 90 mm away from the centre of the circle. Solution : 1. Draw a circle of diameter 50 mm. 2. Locate the point P, 90 mm away from the centre of circle O. 3. Join the points O and P and locate its mid point M. 4. With M as centre and OM as radius draw an arc to cut the circumference of circle at T and T'. 5. Join T with the point P and extend. 6. Now TP is the required tangent to the circle drawn through the point P. Similarly an another tangent T'p can be drawn by joining the points T' and P. 12. To draw a tangent to two circles of equal Radii : Problem : Draw a tangent to two circles of 20 mm radius each, their centres being 60 mm apart. Solution : 1 (External Tangent) (Fig. 4.17) 1. Draw two circles of 20 mm radius each with centres O1 and O2, 60 mm apart. 2. Join the points O1 and O2. 3. Through the points O1 and O2 draw perpendicular lines perpendicular to O1 O2 to cut the circumference of circles at A and B. 4. Join the points A and B and extend it which is the required tangent. Solution 2 : (Internal Tangent) (Fig. 4.18) 1. Draw the circles with 20 mm radius each with centres O1 and O2, being 60 mm apart. 2. Join the points O1 and O2 and locate the mid point M. 3. Locate the Mid point of O1M at N. 4. With N as centre and O1N as radius draw a semi-circle to cut the circumference of circle at P. 5. Join the points O1 and P, and draw a line through O2, parallel to O1P to cut the circumference of second circle at Q in the opposite direction. 6. Join the points P and Q and extend it, which is the required tangent. 13. To draw a tangent to two circles of unequal radii : Problem: Draw a common tangent to two circles having 25 mm and 40 mm radii, centres of circles being 100 mm apart. Solution 1: (External Tangent) (Fig. 4.19) 1. Draw the circles of radii 25 mm and 40 mm, centres being 100 mm apart. (R1= 40 mm ; R2 = 25 mm). 2. Let the centre of larger circle be O1, and the centre of smaller circle be O2. 3. Join O1 and O2. 4. Draw a circle of Radius R1 - R2 (= 15 mm) with O1 as centre. 5. Draw a tangent (Refer : Article 9) through the point O2 to the new circle drawn (radius = 15 mm). Let this tangent pass through the point A. 6. Join the points O1 and A and extend it to meet the circumference of larger circle at B. 7. Draw a line parallel to O1 B through the centre point O2 to meet the circumference of smaller circle at C. 8. Join the points B and C and extend it which is the required external tangent. Solution 2 : (Internal Tangent) (Fig. 4.20) 1. Draw the two circles of radii 40 mm and 25 mm with centres O1 and O2 respectively, which are 100 mm apart. 2. With O1 as centre and radius equal - to R1 + R2 (40 + 25 = 65 mm) draw another circle. 3. Join O1 and O2 and locate the mid point at M. 4. With M as centre and M O1 (or M O2) as radius draw a semicircle to the circumference of third circle (ie., R = 65 mm) to meet at P1. 5. Join P1 and O2. 6. Join P1 and O1 to cut the circumference of circle equal to R1 at P. 7. Draw a line parallel to O1P1 through the point O2 to meet the circumference of circle of Radius R2 at Q. 8. Join the points P and Q and extend it which is the required internal tangent. 14. To construct a triangle of three given sides Problem: Draw a triangle having side 60 mm, 45 mm and 40 mm. Solution : (Fig. 4.21) 1. Draw a straight line AB of length 60 mm. 2. With A as centre and radius 45 mm draw an arc. 3. With B as centre and radius 40 mm draw an arc to cut the arc drawn previously at C. 4. Join the point C with A and B by straight lines to get the required triangle ABC. 15. To Construct an equilateral triangle Problem : Draw an equilateral triangle of side 50 mm. Solution : (Fig. 4.22) (Hint : A triangle having all the three sides equal is known as equilateral triangle) 1. Draw a line AB of length 50 mm. 2. With A as centre and radius equal to 50 mm draw an arc. 3. With B as centre and radius equal to 50 mm draw an arc to cut the arc drawn previously at C. 4. Join C with A and B by straight lines. Now ABC is the required triangle. 16. To Construct a Square of given side Problem : Draw a square of side 50 mm. Solution : (Fig. 4.23) 1. Draw a horizontal line AB of length 50 mm. 2. Erect perpendiculars through the points A and B. 3. With A as centre and radius equal to side of the square draw an arc to cut the perpendicular line drawn through A at D. 4. Similarly with B as centre and radius equal to side of the square draw an arc to cut the perpendicular line drawn through B at C. 5. Join the points D and C. ABCD is the required square. Aliter (By Using Mini Drafter) 1. Draw the line AB of length 50 mm. 2. Set the Minidrafter along the line AB and erect perpendicular from A and B each equal to the side of square, 50 mm to get the points D and C respectively. 3. Join C and D. ABCD is the required square. 17. To Construct a Rectangle of given sides Problem : Draw a rectangle of length 60 mm and width 45 mm. Solution : (Fig. 4.24) The procedure for the construction of square as explained in previous article can be followed by taking the appropriate dimensions of length 60 mm and width 45 mm.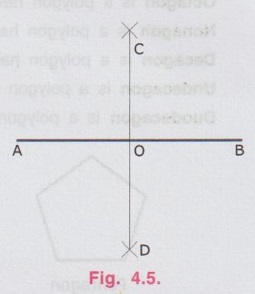
Engineering Graphics: Unit I (a): Geometrical Construction : Tag: : Engineering Graphics (EG) - Review of Simple Geometrical Constructions
Related Topics
Related Subjects
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
