Engineering Physics: Unit II: Electromagnetic Waves
Reflection and Transmission of Electromagnetic waves vacuum - non - conducting medium interface for normal incidence
Let us consider a monochromatic (single frequency) uniform plane wave that travels through one medium (vacuum) and enters another medium (non-conducting) of infinite extent.
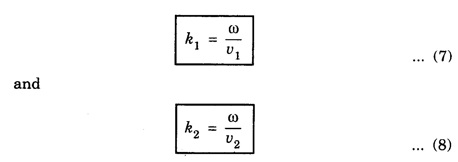
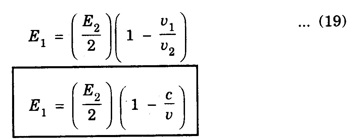
REFLECTION AND TRANSMISSION OF EM WAVES VACUUM - NON - CONDUCTING MEDIUM INTERFACE FOR NORMAL INCIDENCE Let us consider a monochromatic (single frequency) uniform plane wave that travels through one medium (vacuum) and enters another medium (non-conducting) of infinite extent. The uniform plane EM wave propagating along x-direction in a vacuum medium (μ0, ε0) incident normally on the surface of a flat non-conducting medium permittivity, (μ ≠ μ0 and permittivity, ε ≠ ε0). Here the incoming EM wave is called the incident wave, the interface is an infinite plane at x = 0, the region to the left of the interface is medium 1 (x ≤ 0) and the region to the right of the interface is medium 2 (x ≥ 0). At the interface, a part of the incident EM wave will penetrate the boundary (interface) and continue its propagation in medium 2. Now this wave is called the transmitted wave. Another remainder of the wave is reflected at the interface and then propagates in the negative x direction. This wave is called the reflected wave as shown in fig. 2.21. Thus both the incident and transmitted waves propagate in +x direction. The reflected wave will propagate in – x direction. So the incident and reflected waves are in medium 1 and the transmitted wave is in medium 2. Now by considering the electric field If (k1 = ω/v1,) is the propagation constant of this wave (with angular frequency ω and velocity equal to v1) in medium-1, then the electric and magnetic field waves are represented as and Then, the reflected waves are represented as, Here in eqns (3) and (4), the sign is reversed used in the wave number k to denote that this wave is propagating from the interface (boundary) along negative x direction (backward travelling wave). Also the wave numbers k1 and k2 are related to where v1 and v2 are the velocities of EM waves in medium-1 and medium-2 respectively. The total instantaneous electric field The total instantaneous electric field At the interface x = 0, the boundary conditions require that the tangential components of Since the waves are transverse, Also at boundary x = 0, as tangential components are continuous therefore which yields Adding eqns (13) and (17) gives When medium-l is vacuum v1 = c, and v2 = v Subtracting eqn. (17) from eqn. (13) gives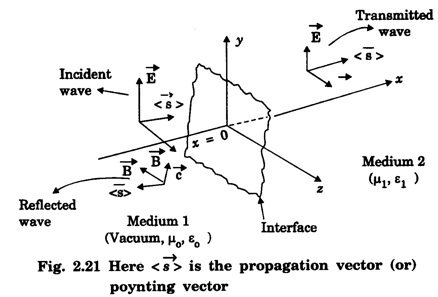
![]() of the incident wave which is polarized in y-direction (plane polarized) and has an amplitude E0 at the interface as shown in fig. 2.21.
of the incident wave which is polarized in y-direction (plane polarized) and has an amplitude E0 at the interface as shown in fig. 2.21.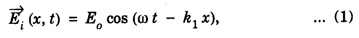
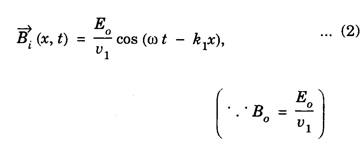
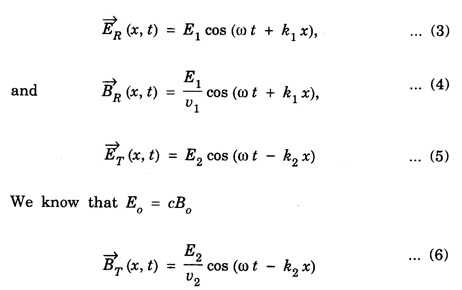
![]() for any value of x with medium 1 is equal to the sum of the incident and reflected waves, so
for any value of x with medium 1 is equal to the sum of the incident and reflected waves, so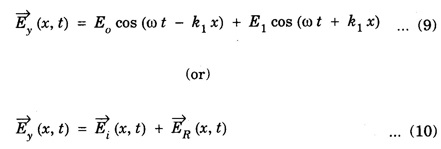
![]() for any value of x in the medium-2 is
for any value of x in the medium-2 is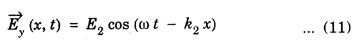
 fields must be continuous.
fields must be continuous.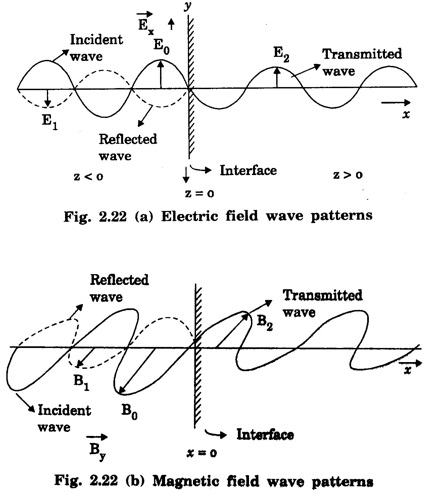
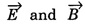 fields are entirely tangential to the interface. Hence at x = 0, eqn. (9) and (10) are equal, so
fields are entirely tangential to the interface. Hence at x = 0, eqn. (9) and (10) are equal, so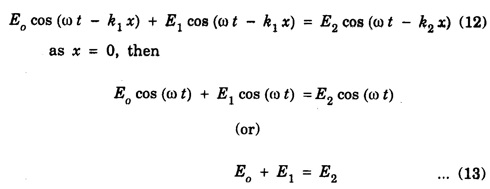
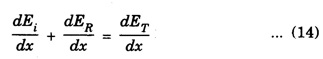

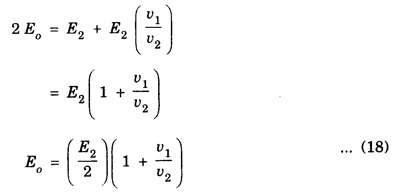
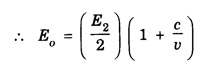
Engineering Physics: Unit II: Electromagnetic Waves : Tag: : - Reflection and Transmission of Electromagnetic waves vacuum - non - conducting medium interface for normal incidence
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
