Engineering Mechanics: Unit III: Distributed Forces
Radius of Gyration
Statement, Diagram, Equation | Moment of Inertia
If the area shown in Fig. 6.1.1 is concentrated into a strip of the same area and is placed parallel to X-axis at a distance Kxx as shown in Fig. 6.2.1
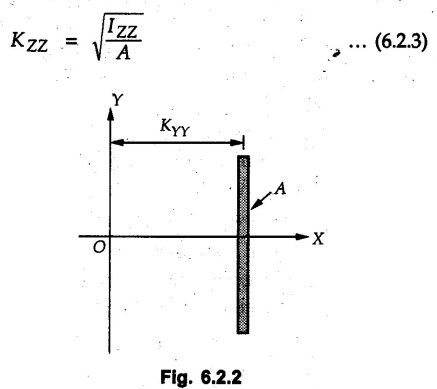
Radius of Gyration • If the area shown in Fig. 6.1.1 is concentrated into a strip of the same area and is placed parallel to X-axis at a distance Kxx as shown in Fig. 6.2.1 such that this strip has the same moment of inertia about X-axis as that of area A, then Kxx is known as the radius of gyration about X-axis. • The moment of inertia can be written for the strip in Fig. 6.2.1 as, • Similarly the radius of gyration can be defined about Y-axis by assuming the area A to be concentrated into a strip parallel to Y-axis at distance KYY: • The radius of gyration about Y-axis is given by Also, in a similar way, the polar radius of gyration Kzz is given by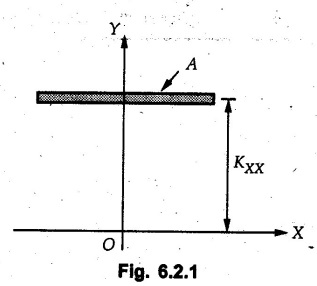


Engineering Mechanics: Unit III: Distributed Forces : Tag: : Statement, Diagram, Equation | Moment of Inertia - Radius of Gyration
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
