Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics
Properties of Fluids
with Solved Example Problems
Every fluid has certain characteristics which describe the physical condition of the fluid.
PROPERTIES OF FLUIDS Every fluid has certain characteristics which describe the physical condition of the fluid. Such characteristics are called properties of fluids. It is the mass of fluid per unit volume. It is also known as mass density (or) specific mass and is denoted by Greek letter ρ (rho). Density (ρ) = Mass (M) / Volume (U) unit in kg/m3 The density of water and air at the standard temperature of 4°C are 1000 Kg/m3 and 500 Kg/m3 respectively. It is the weight of fluid per unit volume. It is also known as weight density and is denoted by w. Specific volume is the volume of fluid per unit mass. It is the reciprocal of density. It is denoted by Us. It is the ratio of density of any given fluid to density of the standard fluid at standard temperature of 4°C. It is also defined as the ratio of specific weight of any given fluid to specific weight of the standard fluid at standard temperature of 4°C. It is also called as relative density and denoted by S. Specific gravity is a mere number and has no units The standard fluid is water for comparing liquid and air is the standard fluid for comparing gases. Specific gravity of water = 1 Specific gravity of mercury = 13.6 Specific gravity of air = 1 Example - 1 Calculate the specific weight, density and specific gravity of two litre of a liquid which weighs 9N. Given data: Volume (U) = 2 Litre = 2/1000 m3 (or) 2 × 10-3 (or) 0.002 m3 Weighs (W) = 9N To find: Specific weight(w), Density (p), Specific gravity(S) Solution: Specific gravity (S) = 0.458 No unit Result : 1. Specific weight (w) = 4500 N/m3 2. Density (p) = 458.71 Kg/m3 3. Specific gravity(S) = 0.458 No unit Example - 2 Calculate the specific weight, mass density, specific gravity and specific volume of oil having a volume of 10000cm3 and weight of 30N. Given data: Volume (U) = 10000cm3 = 10000 / 1000000 m3 (or) 0.01 m3 Weight (W) = 30N To find (i) Specific weight (w) (ii) Mass density (ρ) (iii) Specific gravity (S) (iv) Specific volume (Vs) Solution : Result : (i) Specific weight (w) = 3000 N/m3 (ii) Mass density (ρ) = 305.81Kg/m3 (iii) Specific gravity (S) = 0.305 No unit (iv) Specific volume (U) = 3.27 × 10-3 m3/ Kg It is the resistance offered to the movement of one layer of fluid over another adjacent layer under the action of a shear force. This property of fluid is called viscosity. A fluid is a material which will continues to deform with the application of shear stress. However, different fluid deforms at different rates when the same shear stress is applied. Viscosity is used to determine the amount of resistance to shear stress. The property of viscosity can be seen in the following: 1) We cannot walk fast in water as compared to air as water has comparatively larger viscosity. 2) A stirred liquid comes to rest an account of viscosity. 3) If we pour honey and water on a table then the honey will stop flowing soon while the water will flow for a large distance as it has small viscosity as compared to honey. Considered a fluid placed between two horizontal parallel fluids each of area A and the plates by y apart (Assume the plates to be large enough so that the edge effects may be ignored). Let the upper plate be moved with a velocity U relative to the lower plate by the application of a shearing force F. since the upper plate moves, the fluid particles in contact with the upper plate also move with the velocity U. The lower plate is at rest and the fluid particles in contact with the lower plate are also at rest. Let us consider that the fluid body between the two plates consists of a number of layers parallel to the plates. These different layers of the fluid have different velocity. This results in a continuous shear deformation of the body. 1. Velocity gradient due to viscosity: When a solid mass slides over a surface, a frictional force is developed to oppose the motion, similarly when a layer of a fluid slides over another layer of the same fluid; a frictional force is developed between them opposing the relative motion. This opposite (or) tangential force is called the viscous force. Suppose a fluid is moving in stream lined manner on a fixed horizontal surface AB as shown in the figure 1.3. The layer of the fluid in the contact of the fixed surface remains stationary (at rest), while the velocity of layer increases with distance from the fixed surface. In the figure 1.3, the length of arrows represents the increasing velocity of the layers from the fixed surface. Consider three parallel layers a, b and c from the fixed surface, then their velocities are in the increasing order. The layer a tends to retard the layer b and layer b tends to retard the layer c. Therefore each layer tries to decreases in velocity of the layer above it. It also means that each layer tries to increase the velocity of the layer below it. Therefore there is an internal tangential resistive force acting between the two layers which are opposing their relative motion. This force is called viscous force. In order to maintain the flow of the fluid, we have to apply an external force to overcome this tangential resistive or viscous force. In the absence of external force, the viscous force will resist the flow and bring the fluids to rest. 2. Newton's law of viscosity: The tangential shear stress (τ) existing between two adjacent fluid layers is directly proportional to the velocity gradient (du/dy) in the fluid in a direction perpendicular to the fluid layer. τ α du/dy τ = μ (du/dy) where τ - Shear stress in N/m2 du - Change in velocity in m/s dy - Change in distance or fluid film thickness in m. du/dy - Velocity gradient in S-1 μ - Co-efficient of viscosity (or) Dynamic viscosity in Ns/m2 (or) Absolute viscosity 3. Derivation of Newton's Law of viscosity: A thin layer of fluid which is contained between two parallel plates shown in figure 1.4(a). The upper plate is moved by tangential force F while that lower plate is kept stationary. The movement of upper plate is resisted by the liquid through its viscosity. Therefore the magnitude of velocity of upper plate will depends upon viscosity of the contained fluid in no slip condition, the fluid layer on the lower surface remains stationary where as the top fluid layer moves with the speed of the upper plate. Hence a velocity gradient will act, resulting a vertical fluid line OA deforms to a position OA' as shown in figure 1.4(b). A point B on line OA will move to B' due to its velocity du at a height of dy from B. Now BB' = Velocity × Time = du × dt Also BB' = dy × dθ du × dt = dy × dθ du/dy = dθ/dt where dθ - Angle of deformation in rad dt - Change in Time in sec dθ/dt - Time rate of shear strain per time in S-1 The angle of deformation dθ or strain increases with time but the time rate of shear strain per time (dθ /dt) remain constant as long as force F is unchanged. Shear stress ( τ ) depends up on the applied force (F) and area of contact (A) and it remain constant and it depends upon the time rate of shear strain. τ α dθ/dt τ = μ (dθ/dt) τ = μ (du/dy) du/dy = dθ /dt This is called Newtons equation of viscosity. The fluid which obey this law are called as Newtonian fluids. Otherwise, it is known as non-Newtonian fluids. 4. Dynamic Viscosity (μ): The dynamic viscosity of a fluid may be defined as the shear stress ( τ ) needed to produce unit rate of shear deformation or rate of shear strain (du/dy). It is also called co-efficient of viscosity or absolute viscosity and denoted by Greek letter μ (mu) and its unit is Ns/m2 τ = μ (du/dy) μ = τ /(du/dy) Units: Poise is the unit of viscosity in CGS system 1 Poise = 1/10 or 0.1 Ns/m2 1 Centipoise = 1/100 or 0.01 poise 1 Ns/m2 = 10 Poise 1 kgf - s/ m2 = 98.1 poise Water has viscosity at 20°C = 1 centipoise 5. Kinematic viscosity: It is defined as the ratio between the dynamic viscosity and density of liquid. It is denoted by the letter v (nu) and its unit in m2/s. v = Dynamic viscosity (μ) / Density of liquid (ρ) The kinematic viscosity is the study of motion without regarding the cause of motion and it concerned with length and time only. In liquids the kinematic viscosity decreases with increase in temperature whereas in gases it increases with increase in temperature. Units: The kinematic viscosity in CGS system is stoke 1 stoke = 1cm2/s 1 stoke = 1/104 or 1 × 10-4 m2/s 1 centistoke = 1/106 or 1 × 10-6 m2/s 1 centistoke = 1/100 or 0.01 stoke 6. Variation of viscosity with temperature: The viscosity of a fluid is due to two contributing in factors, namely the cohesion between the fluid molecules and transfer of momentum between molecules. For liquids, the molecules are comparatively more closely packed and molecular activity is rather small. Hence viscosity of liquid is primarily due to molecular cohesion. The inter molecular cohesive force decreases with rise in temperature and hence with the increase in temperature the viscosity of liquid decreases as shown in figure 1.5. For gases the molecular cohesive forces are very small and the viscosity is primarily due to the molecular momentum transfer. The rise of temperature increases the molecular momentum transfer and thereby increases the viscosity of gas. 7. Effect of pressure on viscosity: High pressures also affect the viscosity of a liquid. The viscosity is found to be increasing with rise in pressure. Viscosity increases as more energy is required for the relative movement of liquid molecules at high pressure. 8. Solved Examples based on viscosity: Example - 3 A Mass of liquid weight 400N, is exposed to standard earth's gravity g = 9.806m/s2. (i) What is its mass? (ii) What will be its weight in a planet with acceleration due to gravity is 3.5m/s2? Given data: Weight (W) = 400N Earth's gravity(g) = 9.806m/s2 Planet surface gravity(g) = 3.5m/s2 To find: 1. Mass of liquid in earth surface 2. Weight of liquid in planet surface Solution: Case (i) Earth surface: Mass (m) = Weight (W) / Acceleration due to gravity (g) = 400 / 9.806 = 40.791Kg Case (ii) Planet surface: Weight (W) = mass (m) × Acceleration due to gravity (g) in planet surface = 40.791 × 3.5 (Mass is constant) = 142.769 N Result : 1. Mass of liquid in earth surface (m) = 40.791Kg 2. Weight of liquid in planet surface (W) = 142.769N Example - 4 Determine the specific gravity of a fluid having viscosity of 0.09 poise and kinematic viscosity of 0.052 stokes. Given data: Dynamic viscosity (μ) = 0.09 poise = 0.09 × 0.1 = 0.009N - S/m2 (1 poise = 0.1 N – S/m2) (or) 1/10 N - s/m2 Kinematic viscosity (v) = 0.052 stokes = 0.052 × 10-4 m2/s (1 stokes = 1 × 10-4 m2/s) To find: Specific gravity of a fluid (S) Solution: Specific gravity (S) = 1.730 Example - 5 Calculate the viscosity of a liquid having kinematic viscosity 4 stokes and specific gravity 1.2. Given data: Kinematic viscosity (v) = 4 stokes = 4 × 10-4 m2/sec Specific gravity = 1.2 To find: Viscosity or Dynamic viscosity (μ) Solution: Result : Dynamic viscosity (μ) = 0.48 N - S/m2 Example - 6 If certain oil has density 800Kg/m3, shear stress of a point in oil of 2 × 10-4 KN/m2 and rate of shear stress deformation at that point is 0.5 rad/sec.Calculate the kinematic viscosity of oil in stokes. Given data: Density of oil (ρ) = 800 Kg/m3 Shear stress (τ) = 2 × 10-4 KN/m2 = 2 × 10-4 × 1000 N/m2 = 0.2 N/m2 Shear stress deformation (dθ/dt) = 0.5 rad/sec To find: Kinematic viscosity (v) in stokes Solution : 1. Shear stress (τ) = Dynamic viscosity (μ) × Velocity gradient (du / dy) Velocity gradient (du / dy) = Shear stress deformation (dθ / dt) Shear stress (τ) = Dynamic viscosity (μ) × shear stress deformation Result : Kinematic viscosity (v) = 5 × 10-4 m2/sec (or) 5 stokes Example - 7 The velocity gradient at a certain point of lubricating oil is 0.76S-1. The density of the oil is 1300Kg/m3 and kinematic viscosity is 4 × 10-5m2/sec. Calculate the shear stress at the point and also force. Assume area is 2 m2. Given data: Velocity gradient (du/dy) = 0.76S-1 Density = 1300 Kg/m3 Kinematic viscosity (v) = 4 × 10-5 m2/sec Area = 2 m2. To find: (i) Shear stress (τ) (ii) Force (F) Solution : Result : 1. Shear stress (τ) = 0.03952 N/m2 2. Force (F) = 0.07904 N Example - 8 A plate of 0.35mm from a fixed plate moves at 40 cm/s and dynamic viscosity of oil is 3 poise. Calculate the required force to maintain this speed and area of the plate is 1.5 × 106 mm2 Given data: Distance between the plates (dy) = 0.35mm = 0.35 × 10-3m Velocity of moving plates (u) = 40 cm/s = 0.4m/s Dynamic viscosity (μ) of fluid = 3poise = 0.3 N - S/m2 Area of the plate = 1.5 × 10 mm2 = 1.5m2 To find: Force (F) Solution : Result : Force (F) = 514.285 N Example - 9 The space between two parallel plates 10mm apart is filled with oil. A force of 15N is required to pull the upper plate at a constant velocity of 0.9m/s. Calculate the viscosity of oil, if the area of the upper plate is 2 ×106mm2. Find also the kinematic viscosity of the oil its relative density is 0.8. Given data: Distance between the plates (dy)= 10mm = 10 × 10-3m Velocity of moving plates (u) = 0.9m/s Force = 15N Area of the plate = 2 × 106 mm2 = 2m2 Relative density = 0.8. To find: 1. Dynamic viscosity (μ) of fluid 2. Kinematic viscosity (v) of fluid Solution : = 0.9 - 0 = 0.9 m/s (ii) Change of distance (dy) = 10 × 10-3 m [dy = y because not change in distance] Result : 1. Dynamic viscosity (μ) = 0.083 N - S/m2 2. Kinematic viscosity (v) = 1.04 × 10-4m2/s Example - 10 A body with gravitational force of 400N slides down a lubricated inclined plane making 30oangle with horizontal. The body has a flat surface area of 0.3m2 and slides down at a speed of 2m/s. Determine the lubricant film thickness taking viscosity as 0.3Pa.s. Given data: Force (F) = 400N Inclined plane angle (θ) = 30° Area of the surface (A) = 0.3m2 Speed (or) velocity (u) = 2m/s. Viscosity of oil = 0.3 Pa.s = 0.3 N - s/ m2 [1Pa.s = 1 N - s/m2] To find: The lubricant film thickness (dy) Solution : 1. Weight of the component or force (F) in inclined position = Weight of the component × sin 30° = 400 × sin 30° = 200N Result : Change of oil film thickness (dy) = 9 × 10-4 m Example - 11 A cubical block having 300mm side and mass of 30kg slides down on inclined plane surface which makes an angle of 25° with the horizontal. On the plane, there is a thin film of thickness 0.7mm and viscosity 0.004N-s/ m2. What terminal velocity will be attained by the block? Given data: Cubical block side(s) = 300mm = 0.3m Mass of Cubical block(m) = 30kg Angle of block with the horizontal (θ) = 25° Thin film of oil thickness(dy) = 0.7mm = 0.7 × 10-3 m Viscosity (μ) = 0.004 N - s/m2 To find: Terminal velocity or initial velocity(u) Solution: 1. Area of the cubic plate (A) = side × side = 0.3 × 0.3 = 0.09m2 2. Weight of the component (W) = Mass × Acceleration due to gravity (g) = 30 × 9.81 = 294.3 N 3. Weight of the component or force (F) in inclined position = Weight of the component × Sin 25° = 294.3 × Sin 25° = 124.37N Change of velocity (du) = Velocity gradient × Change of oil film thickness (dy) = 345472.5 × 0.7 × 10-3 = 241.843 m/s 7. Change of velocity(du) = u1 - u2 [u2 = 0] = 241.843 - 0 Terminal velocity or initial velocity (u)=241.843m/s Result : Terminal velocity or initial velocity (u) = 241.843 m/s Example - 12 A 200mm diameter shaft rotates at 1000 rpm in a 100mm long journal bearing 201mm internal diameter. The annular space in the bearing is filled with oil having a dynamic viscosity of 0.17 pa.s. Estimate the power dissipated. Given data: Shaft diameter(D) = 200mm = 0.2m Speed(N) = 1000rpm Length of shaft (L) = 100mm = 0.1m Internal diameter of journal bearing (D1) = 201mm = 0.201m Dynamic viscosity (μ) = 0.17 pa – s = 0.17 N - s/m2 To find: Power dissipated (P) Solution : Result : Power dissipated (P) = 2342.16 Watts Example - 13 A Vertical cylinder of diameter 90mm rotates inside another cylinder concentrically and diameter of outer cylinder is 92mm. The height of the both cylinders are same and equal to 100mm. Find the speed of the inner rotating cylinder, if the space between the cylinders are filled with an oil of viscosity 4poise and torque of 2.47 N-m is applied. Given Data: Inner cylinder diameter(Di) = 90mm = 0.09m Height (or) Length of shaft(L) = 100mm = 0.1m Outer Cyclinder diameter(Do) = 92mm = 0.092m Dynamic viscosity (μ) = 4poise = 0.4N - s/m2 Torque (T) = 2.47 N - m To find: Speed of the inner rotating cylinder (N) Solution: Change of oil film thickness (dy) = (Do – Di)/2 = 0.092 – 0.09/2 = 0.001m 2. Torque (T) = F × (Di/2) Force (F) = T × 2/Di = 2.47 × 2/0.09 = 54.88 N Result: Speed of the rotating inner cylinder (N) = 1029.20 rpm Example - 14 A 20cm diameter vertical shaft rotates concentrically inside the hollow cylinder of diameter 20.3cm. Height is same equal to 40cm. The space between the cylinder and shaft are filled with a liquid. Determine the viscosity of the fluid. The speed of the shaft is 600rpm and Appling force is 200N. Given data: Shaft diameter (d) = 20cm = 0.2m Cylinder diameter (D) = 20.3cm = 0.203m Length of the cylinders (L) = 40 cm = 0.4m Speed of the Rotating inside cylinder (N) = 600rpm Appling force (F) = 200 N To find: The viscosity of the fluid (μ) Solution : Dynamic viscosity (μ) = 0.1899 N – s/m2 Example - 15 The velocity distribution over a plate is given by u = y - y3 in which u is the velocity in m/s at a distance of y meters above the plate, determine the shear stress at y = 0.10m when co-efficient of viscosity is 0.96 N-s /m2. Given data: Velocity profile (u) = y - y3 Distance between the plates (y) = 0.10 m Co-efficient of viscosity (μ) = 0.96 N - s/m2. To find: Shear stress (τ) at y = 0.1m Solution : Shear stress (τ) at y = 0.1m = 0.9312 N/m2 Example - 16 A 50cm diameter vertical shaft rotates concentrically inside the cylinder of diameter 50.5cm.Both shaft and cylinder are 80cm height and the gap filled with the oil. If a toque of 20N-m is required to rotate the shaft of 200rpm, determine dynamic viscosity of oil and the power lost in the cylinder and shaft. Given data: Shaft diameter (d) = 50 cm = 0.5m Cylinder diameter (D) = 50.5cm = 0.505m Height (or) Length of the cylinders (L) = 80 cm = 0.8m Speed of the Rotating inside cylinder (N) = 200rpm Torque (T) = 20N - m To find: 1. Dynamic viscosity of oil (μ) 2. The power lost in the cylinder and shaft (P) Solution: (Drawing is to be similar to previous Example - 19) 1. Tangential velocity(u) = лdN/60 = π × 0.5 × 200/60 = 5.235m/s 2. Change of velocity (du) = u1 - u2 = 5.235 - 0 = 5.235 m/s 3. Change of oil film thickness (dy) = D - d/2 = 0.505 - 0.50/2 = 0.0025m 7. Power dissipated (p) = 2πNT/ 60 = 2 × π × 200 × 20/60 = 418.87 Watts Result : 1. Dynamic viscosity of oil (μ) = 0.0304 N−s/ m2 2. The power lost in the cylinder and shaft (P) = 418.87 Watts Example - 17 A fluid of specific gravity 0.9 flows along a surface with a velocity profile given by u = 2y-6y3 m/s, where y is in m what is the velocity gradient at the boundary? If the kinematic viscosity is = 0.26 stokes, what is the shear stress at the boundary? Given data: Velocity profile(u) = 2y - 6y3 Specific gravity = 0.9 Kinematic viscosity (v) = 0.26 stokes = 0.26 × 10-4 m2/s To find: Velocity gradient at the boundary (du/dy) y = 0 Shear stress at the boundary (τ) at y = 0 Solution : 1. Velocity profile (u) = 2y - 6y3 Result : 1. Velocity gradient at the boundary (du/dy) at y = 0 = 2S-1 2. Shear stress (τ) at y = 0 = 0.0468 N/m2 Example - 18 If the velocity profile of a fluid over a plate is parabolic with the vertex 30cm from the plate, where the velocity is 100cm/sec. Calculate the velocity gradients and shear stresses at a distance of 0.15 and 30cm from the plate, if the viscosity of the fluid is 7.5 poise. Given data: Distance from vertex from the plate (y) = 30cm= 0.3m Velocity at vertex (u) = 100cm/sec = 1m/sec Viscosity of the fluid (μ) = 7.5 poise = 0.75N - s/m2 To find: 1. The velocity gradients (du/dy) at y = 0, y = 15 and y = 30cm 2. Shear stresses (τ) at y = 0, y = 15 and y = 30cm Solution : 1. The given velocity profile is parabolic. So that the equation for the given velocity profile is u = ay2 + by + c ... (X) . Where a,b and c are constants. These values are determined from following boundary conditions. (i) u = 0 at y = 0 (ii) u = 1 m/s at y = 0.3m (iii) du/dy = 0 at y = 0.3m 2. Substituting boundary conditions (i) in equation (X) u = ay2 + by + c [u = 0 at y = 0] 0 = a(0)2 + b(0) + c = 0 + 0 + c C = 0 Substituting boundary conditions (ii) in equation (X) u = ay2 + by + c [u = 1 at y = 0.3] 1 = a (0.3)2 + b(0.3) + c 1 = 0.09a + 0.3b + c (c = 0) 1 = 0.09a + 0.3b …(Y) Substituting boundary conditions (iii) in equation (X) u = ay2+ by + c du/dy = 0 at y = 0.3m du/dy = 2ay + b 0 = 2a × 0.3 + b = 0.6a + b b = - 0.6a . ….(Z) Substituting the values of b in equation (X) 1 = 0.09a + 0.3b [b = - 0.6a] 1 = 0.09a + 0.3 (-0.6a) 1 = 0.09a - 0.18a = -0.09a a = - 11.11 Substituting the value of (a) in equation (Z) b = - 0.6a [a =- 11.11] b = -0.6 × - 11.11 b = 6.666 Substituting a,b and c value in equation (X) u = ay2 + by + c u = - 11.11y2 + 6.666y + 0 du/dy = -22.22y + 6.666 Velocity gradients (du/dy)at y = 0 = -22.22 × 0 + 6.666 = 6.666 S-1 (du/dy) at y = 0.15 (-22:22 × 0.15) + 6.666 = 3.33 S-1 (du/dy) at y = 0.30 = (-22.22 × 0.3) + 6.666 = 0 S-1 5. Shear stresses (τ)at y = 0, y = 15 and y = 30cm Result : 1. Velocity gradients (du/dy) at y = 0 = 6.666 S-1 (du/dy) at y = 0.15 = 3.33 S-1 (du/dy) at y = 0.30 = 0 S-1 2. Shear stresses (τ) Shear stresses (τ) at y = 0 = 4.999 N/m2 Shear stresses (τ) at y = 0.15 = 2.4975 N/m2 Shear stresses (τ) at y = 0.30 = 0 N/m2 Example - 19 Determine the intensity of shear stress of an oil having viscosity =3poise. The oil is used for lubricating the clearance between a shaft of diameter 0.20m and its journal bearing. The clearance is 2.5mm and the shaft rotates at 250rpm. Given data: Dynamic viscosity (μ) = 3poise Shaft diameter (D) = 0.20m Clearance between shaft and journal bearing (dy) = 2.5mm = 2.5 × 10-3m Speed of the shaft (N) = 250 rpm To find: Shear stresses (τ) Solution : Result : Shear stress (τ) = 314.04 N/m2 Example - 20 A thin plate is moving between the two fixed surface with the oil of viscosity μ1, on the top side of the plate and viscosity μ2, on the bottom side of the plate respectively from the fixed surface. The height between the surface is h and the plate moving constant velocity is u .Derive an expression for the position of the plate so that; (i) The shear force on the both side of the plate is same (ii) The minimum force is required to drag the plate Given data: Viscosity of the oils = μ1 and μ2 Velocity of the plate įs = u Height between the surface = h To find: The position of the plate (i) The shear force on the both side of the plate is same (ii) The minimum force is required to drag the plate Solution : 1. Shear stress is required per unit area on the upper side of the plate (τ1) τ1 = μ1 × du/dy du = u dy = (h-y) τ1 = μ1 × u/(h-y) ... (i) 2. Shear stress is required per unit area on the bottom side of the plate (τ2) τ2 = μ2 × du/dy du = u dy = y τ2 = μ2 × u/y ... (ii) 3. Shear force is required per unit area on upper side of the plate (F1) (F1) = Shear stress × Area of the plate = μ1 × u/(h−y) × A 4. Shear force is required per unit area on the bottom side of the plate (F2) (F2) = Shear stress × Area of the plate = μ2 × u/y × A 5. Case (I) The shear force is equal on two side of the plate F1 = F2 μ1 × u/(h−y) × A = μ2 × u/y × A (Area of the plate is same) μ1 × u̸/(h–y) = μ2 × u/y y/(h−y) = μ2 × u/μ1 × u y/ (h−y) = μ2/μ1 у μ1 = μ2 (h - y) у μ1 = μ2 h - μ2 y у μ1 + μ2y = μ2 h у (μ1 + μ2) = μ2 h y = μ2 h/(μ1 + μ2) 6. Case (II) The minimum force is required to drag the plate (i) Total force required (F) = Force required on upper side (F1) + Force required on bottom side (F2) = [Shear stress (τ1) × A] + [Shear stress (τ2) × A] = [μ1 × u/(h-y) × A] + [μ2 × u/y × A] F = μ1 × u/(h−у) + μ2 × u/y Force (F) is to be minimum, dF/dy = 0 Result: The position of the plate The shear force on the both side of the plate is same The minimum force required = Example - 21 The thin plate of area 'A' is Placed midway in a gap of two fixed surface of height h filled with a liquid of viscosity μ1 on both side of the plate. The same gap is filled with another liquid of viscosity μ2 and the same plate is fixed not in the mid way between the gap but parallel to the fixed surface. Same velocity for the both position of the plate fixed in the gap and the force required was same to move the plate. Prove that Area of the plate = A Viscosity of the plate = μ1 and μ2 Height of the plate = h To find: Prove that = Solution : Case 1: When the plate is placed midway of the surfaces and oil of viscosity μ1 1. Shear force on the upper side of the plate (Fu) = shear stress (τ) × Area of the plate (A) 2. Shear force on the bottom side of the plate (Fb) = Shear force on the upper side of the plate (Fu) (due to equal distance and same fluid is used on both side of the plate) 3. Total force acting on the both side of the plate (F1) = (Fu) + (Fb) Case 2: When the plate is not placed midway of the surfaces and another oil of viscosity μ2 Example - 22 Two large fixed parallel planes are 16mm apart. The space between the surfaces is filled with oil of viscosity 0.82N-s/ m2. A flat thin plate 0.30 m2 area is moved through the oil at a velocity of 0.5 m/s. Calculate the force required to move the plate (i) When the thin plate is middle of the space between the surfaces. (ii) When the thin plate is at a distance of 6mm from the upper planes. Given data: Distance between the fixed planes (y) = 16mm = 0.016 Area of the thin plate = 0.30m2 Velocity of moving plate (u) = 0.5m/s Viscosity of oil (μ) = 0.82 N - s/m2 To find: Force required to moving the plate 1. When the thin plate is middle of the space between the surfaces 2. When the thin plate is at a distance of 6mm from the upper planes. Solution : Case II: The plate is fixed at a distance of 6mm from the upper planes (i) Shear stress on the upper side of the plate = (μ) × (du/dy) Change of velocity (du) = u = 0.5m/s Change of oil film thickness(dy) = y1 - y2 (y2 = 0) dy = y1 The plate is 0.006m from the upper planes so y1 = 0.006m dy = 0.006m (τ1) = 0.82 × (0.5/0.006) (τ1) = 68.33N/m2 (ii) Force on upper side of the plate (F1) = Shear stress (τ1) × Area of the thin plate = 68.33 × 0.30 = 20.499N (iii) Shear stress on the lower side of the plate (τ2) = (μ) × (du/dy) Change of velocity(du) = u = 0.5m/s Change of oil film thickness (dy) = y1 − y2 (y2 = 0) (dy) = y1 (The plate is 0.01m from the lower planes so y1 = 0.010 m) dy = 0.010m (τ2) = 0.82 × 0.5/0.01 (τ2) = 41N/m2 (iv) Force on upper side of the plate (F2) = Shear stress (τ2) × Area of the thin plate = 41 × 0.30 12.3N (v) Total force required (F) = F1 + F2 = 20.499 + 12.3 = 32.799N Result : 1. Force required to plate is middle of the gap between the planes = 30.75N 2. Force required to plate is at a distance of 6mm from the upper planes = 32.799N. Example - 23 Two large fixed parallel surfaces are 20mm apart and the space between the surfaces is filled with oil. If the dynamic viscosity of the two side oils are in the ratio of 1:4 and viscosity of bottom oil is 0.40N-s/m2. Determine the velocity of the centrally fixed plate at which the central plate will move. The central plate of area 8m2 being pulled with a force of 180N. Given data: Distance between the fixed plane surfaces (y) = 20mm = 0.020m Area of the thin plate = 8m2 Viscosity of oil at bottom surface (μ2) = 0.40 N-s/m2 Viscosity ratio of fixed surfaces = 1:4 Applied force (F) = 180N To find: Velocity of the moving plate (u) Solution : 1. Shear stress on the top side of the plate (τ1) = (μ1) × (du/dy) (i) Change of velocity (du) = u (ii) Change of oil film thickness (dy) = y1 – y2 [y2 = 0] dy = y1 (The plate is fixed midway so y1 = y/2) = y/2 = 0.020/2 = 0.010m (iii) Viscosity of oil at top side (μ1) = 1 × Viscosity of oil in bottom side = 1 × 0.40 = 0.40 N-s/m2 (τ1) = 0.40 x (u/0.010) (τ1) = 40u 2. Force on upper side of the plate (F2) = Shear stress (τ2) × Area of the thin plate = 40u × 8 = 320u 3. Shear stress on the bottom side of the plate (τ2) = (μ2) × (du/dy) (i) Change of velocity (du) = u [u2 = 0] (ii) Change of oil film thickness (dy) = y1 - y2 [y2 = 0] dy = y1 (The plate is fixed midway so y1 = y/2) = y/2 = 0.020/2 = 0.010m (iii) Viscosity of oil at top side (μ2) = 4 × Viscosity of oil in bottom side = 4 × 0.40 = 1.6 N-s/m2 (τ2) = 1.6 × (u/ 0.010) = 160 u 4. Force on bottom side of the plate (F2) = Shear stress (τ2) × Area of the thin plate = 160 u × 8 = 1280 u 5. Total force (F) = F1 + F2 180 = 320 u + 1280 u = 1600 u 6. Velocity of the plate (u) = 180/1600 = 0.1125 m/s Result : Velocity of the plate(u) = 0.1125 m/s Example - 24 A metal plate 2m × 2m × 8mm dimension and weighing 300N is place midway in 30mm between the two vertical planes. The gap between the plane surfaces are filled with oil of specific gravity 0.85 and dynamic viscosity 5N-s/ m2. Determine the force required to lift the plate with a constant velocity of 0.3m/s. Given data: Distance between the fixed surfaces (y) = 30mm = 0.030m Area of the thin plate = 2 × 2 = 4 m2 Thickness of the plate = 8mm = 0.008m Viscosity of oil(u) = 5 N-s/m2 Velocity of oil(u) = 0.2m/s Weight of the plate(W) = 300N Specific gravity of oil(S) = 0.85 To find: Force required to lifting the plate (F) Solution: 1. Distance from the fixed left side surface to metal plate (y1) Change of velocity (du)1 = u = 0.2 m/s Change of oil film thickness (dy)1 = y1 = 0.011m (τ1) = 5 × (0.2/0.011) = 90.909 N/m2 4. Shear force on left side of the plate (F1) = τ1 × A = 90.909 × 4 = 363.63N 5. Shear force of right side (F2) = Shear force of left side (F1) [plate is fixed center of the planes] (F2) = 363.63N 6. Upward thrust (or) Buoyance force on the plate = Specific weight of oil × Volume of oil displaced = (Specific gravity of oil × specific weight of water) × (Area of the plate × Thickness of the plate) = ( 0.85 × 9810) × (4 × 0.008) = 266.832N 7. Effective weight of the plate = weight of the plate - Upward thrust = 300 - 266.832 = 33.168N 8. Total force required to lift the plate = F1 + F2 + Effective weight of the plate = 363.63 + 363.63 + 33.168 = 760.428 N Result : Force required to lifting the plate (F)= 760.428 N Example - 25 A circular disc having radius R is kept at small height h above a fixed surface by a layer of oil having viscosity μ . Determine the expression for the viscous torque on the side and power necessary to maintain ω angular velocity. Given data: Disc radius = R Viscosity = μ angular velocity = ω Height = h To find: 1. Torque (T) 2. Heat dissipation (or) Power (P) Solution : In order to find viscous torque, we take an elementary ring at radius r and thickness dr. If ω is angular velocity of the disc, the tangential velocity at ring is u = rω and area of the ring is 2πr.dr Example - 26 A solid cone of radius R and vertex angle of 2θ is made to rotate at angular velocity ω in the conical cavity containing oil with viscosity μ . If h is the gap between the cone and cavity, find torque T to rotate the cone and the rate of heat dissipation in the bearing. Given data: Radius of cone = R Angular velocity = ω Vertex cone = 2θ Viscosity = μ Gap between the cone and cavity = h To find: 1. Torque (T) 2. Heat dissipation (or) Power (P) Solution: (i) Consider an small element between a radius r + dr of area dA and slant height ds of the cone Sin θ = dr/ds Slant height (ds) = dr/Sin θ (ii) Area (dA) = 2 πr ds = 2 πr × (dr/Sin θ) (iii) Shear stress (τ) = μ × du/dy (du = u and dy = h) (τ) = μ × u/h (iv) Shear force (dFr) = Shear stress (τ) × Area (dA) = μ × (u/h) × (2 лг × (dr/Sinθ)) (v) Torque (dTr) = F × d/2 (r = d/2) = μ × (u/ h) × ( 2 πr × (dr / Sin θ) ) × r = μ × (ω r/h) × (2 πr × (dr/Sin θ) xr [u = ω × t] Result : Example - 27 The shaft of diameter D and length L rotating at taper bearing. The clearances at the ends are h1 and h2 respectively. The oil has a viscosity of μ and the shaft μ moves axially at a velocity u .Derive an expression for the force required for axial movement of the shaft through a taper bearing. Given data: Diameter = D Viscosity = μ Length = L Velocity = u Clearances = h1 and h2 To find: Derive an expression for the force required for axial movement of the shaft Solution: The clearance varies along the length so the velocity gradient will vary↓ along the length and also the shear stresses vary along the length. Consider a small element of distance x from the h1 clearances and length dx. 1. The clearance at the element x, Result: Example - 28 A 150mm diameter disc rotates over a flat surface separated by an oil film of 0.8mm thickness. Calculate the viscosity of oil, if the torque required to rotate the disc at 200rpm was 1.2N-m. Given data: Diameter of disc, D = 150mm = 0.15m Oil film thickness, y = 0.8mm = 0.0008m Speed of disc, N = 200 rpm Torque, T = 1.2 N-m To find: Viscosity of oil (μ) Solution: Result : Viscosity of oil, μ = 0.9224 N-s/m2 Example - 29 Find the required oil film thickness between the plates of a collar bearing to transmit 100W power at a speed of 1000rpm. The outside and inside diameters of the collar bearing are 650mm and 500mm. The oil used has a viscosity of 0.4 . poise. Given data: Power to be transmitted, P = 100W Speed, N = 1000 rpm Outside diameter of collar bearing, D=650mm = 0.65m Inside diameter of collar bearing, Do = 500mm = 0.50m Viscosity of oil, μ = 0.4 poise = 0.04 N-s/m2 To find: Oil film thickness, y Solution: Oil film thickness, y = h = 1.3628 × 10-5 m Example - 30 A conical bearing of outer radius 600mm, inner radius 450mm and height 150mm runs on a conical support with a uniform clearance between surfaces. The clearance between bearing and support is filled with oil of viscosity 70CP is used. The support is rotated at 500rpm. Determine the clearance, if the power required was 2KW. Given data: Outer radius, Ro = 600mm = 0.6m Inner radius, Ri = 450mm = 0.45m Length (or) Height, (L) = 150mm = 0.15m Viscosity of oil, (μ) = 70CP = 70/100 = 0.7 poise = 0.07N - s/m2 Speed, N = 500 rpm Power, P = 2KW To find: Clearance Solution : Result : Clearance, h = 18.8772 × 10-3m Example - 31 The clearance between the shaft of 100mm diameter and the bearing varies from 4mm to 2mm over a length of 1m. The viscosity of oil filling the clearance is 0.06N-s/m2 The axial velocity of the shaft is 0.7 m/s. Determine the force required for axial movement of the shaft. Given data: Diameter of shaft, D = 100mm = 0.1m Maximum clearance, h1 = 4mm = 0.004m Minimum clearance, h2 = 2mm = 0.002m Length of shaft, L = 1m Viscosity of oil, μ = 0.06Ns/m2 Axial velocity, u = 0.7m/s To find: Force required for the axial movement of the shaft Solution: Result : Force required for the axial movement of the shaft is 4.5729 N Compressibility is the property of a fluid, which characterizes its ability to change its volume under pressure. It is also defined as the fluid undergoes change in volume under the action of external pressure. Fluids can be compressible or incompressible. Incompressible fluids have constant density and compressible fluids have variable density. From figure 1.6, In compressible fluids, when pressure is applied, fluid contracts (decrease in volume = dv) and when pressure is reduced, they expand (initial volume = U). The compressibility in fluid mechanics is considered mainly when the velocity of flow is high. 1. Co-efficient of Compressibility (β) It is the ratio of the change of volume per unit volume i.e. volumetric strain to change of pressure. The negative sign of the volumetric strain indicates the decrease in volume with the increase in pressure. It is also called as the reciprocal of bulk modulus of elasticity. The bulk modulus of elasticity is defined as the ratio of the change of pressure to volumetric strain. It is also called as the reciprocal of the compressibility. Elasticity of fluid is measured in terms of bulk modulus. It is also expressed in terms of change of density. The bulk modulus of the liquids depends on pressure and temperature. Relationship between bulk modulus (K) and pressure (P) for a gas: (i) Isothermal process: For isothermal process PU = Constant Partially differentiating the above equation PdU + UdP = 0 PdU = - UdP P = -UdP/dU P = k, For isothermal process. (ii) Adiabatic process For adiabatic process PUγ = Constant (γ = Ratio of specific heat) Partially differentiating the above equation Surface tension is defined as the tensile force acting on the surface of a liquid in contact with a gas or on the surface between two immiscible (not mixable) liquids such that the contact surface behaves like a membrane under tension. The magnitude of this force- per unit length of free surface will have the same value as the surface energy per unit area. When a liquid is filled inside a narrow tube, the free surface of the liquid displays either a rise (or) fall nears the walls of the tube. This phenomenon is attributed to a property of fluids known as surface tension. Soap bubbles, small droplets of water and dew on a dry solid surface also are attributed to surface tension. Surface tension in a liquid is caused by cohesion and adhesion. The value of surface tension depends upon the following factors. (i) Nature of the liquid, (ii) Nature of the surrounding matter (solid, liquid and gas), (iii) Kinetic energy. Cohesion: Cohesion means intermolecular attraction between molecules of the same liquid or same solid surface. Example for cohesive force: When mercury is poured on the floor, it does not wet the surface of floor and forms sphere. When two spheres of mercury are brought close together, they combine together to form a bigger sphere. This means that the mercury have cohesive force. Adhesion: Adhesion means attraction between the molecules of the different liquid or molecules of a liquid and solid surface. Example for adhesive force: When water is poured on the floor, the water molecules wet the surface. This means that water molecules have adhesive tendency to adhere to the floor. (Solid surface) Consider a liquid in a vessel as shown in figure 1.7 (a) Consider two molecules as A and B in a mass of liquid. The molecule A is attracted in all directions equally by the surrounding molecules of the liquid. Thus the resultant force acting on the molecules A is zero. But the molecule B is situated near the free surface. This molecule B is acted upon by upward and downward forces which are unbalanced. Thus net resultant force on molecule B is acting in a downward direction and all the molecules near the free surface experience a downward force. So the free surface of the liquid acts likes a very thin film under tension of the surface of the liquid. Similar reason incase of contact surface between two immiscible liquids as shown in figure 1.7(b). Examples of phenomenon of surface tension: (i) Rain drops. (ii) Rise of sap in a tree. (iii) Bird can drink water from ponds. (iv) Capillary rise and depression in thin- bored glass tubes. (v) Collection of dust particles on water surface. (vi) Break up of liquid jets. (vii) Formation of dew drops on grass early morning. (viii) Floating of a greased needle of steel on water surface. The value of surface tension depends upon the following factors; (i) Nature of the liquid. (ii) Nature of the surrounding matter. (iii) Kinetic energy. 1. Surface tension on liquid droplet: Consider a small spherical droplet of a liquid as shown in figure 1.8 (say a rain drop) of diameter d and let it be cut into two halves. On the entire surface of the droplet, the tensile force due to surface tension will be acting. Let, P = Pressure inside the droplet above outside pressure σ = Surface tension of the liquid d = Diameter of the droplet The forces acting on one-half (say left half) will be (i) Pressure force P × π/4 × d2 (ii) Surface tension force acting around the circumferencе = σ × πd Under equilibrium conditions these two forces will be equal and opposite From the above equation increase of droplet diameter and decrease of pressure intensity inside the droplet increases. 2. Soap (or hollow) bubble: A soap bubble has two surfaces in contact with air i.e., inside and outside. Surface tension will act on both the surfaces. Figure 1.9 shows the Soap (or hollow) bubble. Let us consider a cylindrical liquid jet of diameter (d) and length (L) as shown in figure 1.10. 1. Effect of temperature on surface tension: Surface tension depends directly upon the intermolecule at cohesion since this' cohesion decreases with rise in temperature, thus surface tension decreases with temperature rise. Capillarity is defined as a phenomenon of rise or fall of a liquid surface in a small tube relative to the adjacent general level of liquid when the tube is held vertically in the liquid. Capillarity is the property of exerting forces on fluids by fine tubes. It is due to cohesion and adhesion. The rise of liquid surface is known as capillary rise and the fall of the liquid surface is known as capillary fall. Capillarity depends upon the following factors 1. Specific weight of the liquid 2. Diameter of the tube 3. Surface tension of the liquid 1. Expression for capillary rise: Consider a glass tube of small diameter d, opened at both ends and is inserted in liquid, say water. The liquid will rise in the tube above the level of liquid shown in figure 1.11 (a). Upward surface tension force (lifting force) = σ cos × Circumference of the tube 0 = σ × πd × cos θ Weight of the liquid of height h in the tube = Mass of liquid × Acceleration due to gravity(g) = Volume (U) × density (ρ) × g = Area of the tube (A) × Height of the liquid in the tube (h) × ρ × g = π/ 4 d2 × hρg Under equilibrium condition, equate both forces σ × лd × cos θ = π/ 4 d2 × h ρ g Capillary rise (h) (For water θ = 0) (h) = 4σ / wd d - Diameter of the capillary tube θ - Angle of contact of the water surface σ - Surface tension force for unit length w - Weight density (ρ g) 2. Expression for capillary fall or depression: The glass tube is dipped in mercury, the level of mercury in the tube will be lower than the general level of the out side tube shown in figure 1.11 (b). Hydrostatic force acting upward (π/4) d2 × h ρ g Downward force making depression due to surface tension = σ × лd × cosθ Under equilibrium condition, σ × лd × cosθ = (π/4)d2 × h ρ g Capillary fall (h) = 4 σ cosθ / ρgd (The value of θ = 128°) A change from the liquid state to the gaseous state is known as vaporization. The vaporization takes place due to liquid molecules continuous escaping from the free liquid surface. Consider a liquid (water) is kept in a closed vessel at atmospheric conditions. This liquid will vaporize at 100° c as shown in figure 1.12. When vaporization takes place, the molecules escaps from the free surface (top surface) of the liquid. This vapour molecules occupies the space between the free surface of the liquid and top of the vessel. This vapour exerts a partial pressure on the surface of the liquid. This pressure is known as vapour pressure of liquid. Example - 32 The volume of oil in hydraulic cylinder with piston arrangement is 0.6 m3 and the pressure is 20kN/m2. The piston diameter is 30cm. Determine the distance through which the piston has to move so that the pressure will increase to 100kN/ m2. Take bulk modulus as 3150 × 103N/m2. Given data: Initial volume (U) = 0.6m3 Initial pressure (p1) = 20kN/m2 = 20,000 N/m2 Final pressure (p2) = 100,000 N/m2 Piston diameter (d) = 30cm = 0.3m Bulk modulus = 3150 × 103 N/m2. To find: The distance through which the piston has to move Solution : 1. Change in pressure (dP) = p2 - p1 = 100,000 - 20,000 = 80,000 N/m2 2. Bulk modulus (K) = dp / (dU/U) dU/U = K × dp = 80,000/3150 × 103 dU/U = 0.02539 Change in volume (dU) = 0.02539 × U = 0.02539 × 0.6 dU = 0.0152m3 3. Area of the cylinder (A) = π/ 4 × d2 = π/4 × (0.3)2 = 0.0706 m2 Change in volume (dU) = Area of the cylinder (A) × Piston movement (L) 4. Piston movement (L) = Change in volume (dU) /Area of the cylinder (A) = 0.01523/0.0706 = 0.215m Result : Piston movement (L) = 0.215m Example - 33 Density of storage water in the reservoir at the top surface was measured as 1000kg/m3 and atmospheric pressure is 101.325 KN/m2. At certain depth in water, the density was found to be 1050kg/m3. Determine the pressure at that point. The bulk modulus for the storage water is 23Gpa. Given data: Density of water in top surface of the reservoir (ρ1) = 1000kg/m3 Pressure of water in top surface of the reservoir (P1) = 101.325KN/m2 = 101325 N/m2 Density of water at certain depth of the reservoir(ρ2) = 1050kg/m3 Bulk modulus (K) = 23Gpa = 23 × 109 N/m2 To find: The pressure at certain depth that (P2) Solution: 1. Volumetric strain = (dU/U) (dU/U = dρ/ ρ1) = d ρ/ ρ1 = ρ1 – ρ2 / ρ1 [dρ = ρ1 – ρ2] = 1050 – 1000/1000 Volumetric strain (dρ/ ρ1) = 0.05 2. Bulk modulus (K) = dρ/ -dρ/ ρ 3. Change in pressure (dP) = Bulk modulus (K) × dρ/ ρ Change in pressure (dP) = 23 × 109 × 0.05 Change in pressure (dP) = 1.15 × 109 N/m2 4. Change in pressure (dP) = P1 – P2 Final pressure (P2) = dP + P1 = 1.15 × 109 + 101325 = 1.150 × 109 N/m2 Result : Final pressure (P2) = 1.150 × 109 N/m2 Example - 34 An increase in pressure of a liquid from 9MPa to 14MPa results into 0.6% decrease in its volume. Find bulk modulus and co-efficient of compressibility. Given data: Initial pressure (P1) = 9 MPa = 9 × 106 N/m2 Finial pressure (P2) = 14MPa = 14 × 106 N/m2 Volumetric strain (dU/U) = 0.6/100 = 0.006 To find: 1. Bulk modulus (k) 2. Co-efficient of compressibility (β) Solution : = 1.2 × 10-9 m2/N Result : 1. Bulk modulus(K) = 8.33 ×108 N/m2 2. Co-efficient of compressibility (β) = 1.2 × 10-9 m2/N Example - 35 The fluid co-efficient of compressibility is 1.5 × 109 m2/N is filled in a reservoir of capacity 0.13m3. When will the pressure reduce when some amount of fluid will spill over, if the pressure in the reservoir is reduced by 20Mpa. Calculate the amount of fluid that will spill over. Given data: Co-efficient of compressibility (β) = 1.5 × 10-9 m2/N Reservoir capacity (U) = 0.13m3 Reduce pressure (dp) = -20MPa = -20 × 106 To find: The amount of fluid that will spill over (dv) Solution : Co-efficient of compressibility (β) = (dU/U)/ dp = Change in volume (dU) = β × U × dp = 1.5 × 10-9 × 0.13 × 20 × 106 = 0.0039m3 Result : Change in volume (dU) or The amount of fluid that will spill over = 0.0039 m3 Example - 36 A cylinder contains 0.6m3 air at 100KN/m2 which is compressed to 0.08 m3. Find bulk modulus if compression is done isothermally and adiabatically. Take γ = 1.4 Given data: Initial volume (U1) = 0.6m3 Final volume (U2) = 0.08m3 Initial pressure (p1) = 100kN/m2 = 100,000 N/m2 Ratio of specific heats (γ) = 1.4 To find: Bulk modulus (K) when 1. Process isothermally 2. Process adiabatically Solution : 1. Process isothermally P1 U1 = P2U2 P2 = P1 U1/U2 = 100,000 × 0.6/0.08 P2 = 7.50 × 105 N/m2 Bulk modulus (k) = P2 = 7.50 × 105 N/m2 2. Process isothermally P1 U1 γ = P2U2 γ P2 = P1 (U1 / U2) γ = 100,000 × (0.6/0.08)1.4 P2 = 1.679 × 106 N/m2 Bulk modulus (k) = P2 = 1.679 × 106 N/m2 Result : Bulk modulus (K) when 1. Process isothermally (k) = 7.50 × 105 N/m2 2. Process adiabatically (k) = P2 = 1.679 × 106 N/m2 Example - 37 Calculate the capillary rise in a glass tube of 5.5mm diameter when immersed vertically in (a) water and (b) mercury. Take surface tension of water and mercury as 0.0925 N/m and 0.65N/m respectively. The specific gravity for mercury is given as 13.6 and angle of contact = 130o. Given data: Glass tube of diameter = 5.5mm = 5.5 × 10-3m Surface tension of water (σw) = 0.0925 N/m Surface tension of water (σm) = 0.65N/m Specific gravity for mercury (Sm) = 13.6 Angle of contact of mercury (θm) = 130° To find: 1. Capillary rise for water 2. Capillary rise for mercury Solution: Result : 1. Capillary rise for water (h) = 0.00685m 2. Capillary rise for mercury (h) = -0.00227m Example - 38 Two capillary tubes of diameter 10mm and 7mm are held vertically inside water one by one. How much high the water will rise into each tube. Take σw = 9 × 10−2 N/m Given data: First tube diameter (d1) = 10mm = 0.01m Second tube diameter (d2) = 7mm = 0.007m Surface tension for water (σw) = 9 × 10-2 N/m To find: The rise of water in the each tube h1 & h2 Solution : 2. h1d1 = h2d2 Result : The rise of water in the each tube h1 = 3.66 × 10-3 m & h2 = 5.242 × 10-3 m Example - 39 A U tube has two limbs of internal diameter of 10 & 20 mm respectively the tube contains water. Find the difference of level in the limbs. If σw = 0.095 N/m. Given data: Left limb tube diameter, d1 = 10mm = 0.01 m Right limb tube diameter, d2 = 20mm = 0.02 m Surface tension of water, σw = 0.095 N/m To find: The difference of level in the limbs (H) Solution : Water will rise more in small diameter limb, so the difference of water level in the limb is H = h1 - h2 Result : The difference of level in the limbs, H = 1.936 × 10-3m Example - 40 In a closed end single tube manometer, the height of mercury column above the mercury shows 760mm against atmospheric pressure. The diameter of the tube is 5mm and angle of contact is 130°. Determine the actual height representing the atmospheric pressure. If surface tension is 0.60 N/m. Given data: Height of the mercury column = 760 mm Angle of contact θ = 130° Diameter of the tube d = 5mm = 0.005 m Surface tension σ = 0.60 N/m To find: Actual height of mercury column Solution : 1. Specific gravity of mercury(s) = Specific weight of mercury/specify weight of water Specific weight of mercury(s) = Specific gravity of mercury × specify weight of water = 13.6 × 9810 = 133416 N/m3 3. Actual height of mercury column = manometer height + capillary depression = 760 - 2.312 = 757.688 mm Result: Height of mercury column=757.688 mm Example - 41 A differential U tube manometer in a glass tubing of various diameters is used to measure pressure. The diameters of glass tubes are 7mm and 9mm. The manometer is used to measure readings in the range of 50mm to 170mm. calculate the percentage of error that can creep in the highest and lowest readings. Take surface tension = 0.090 N/m and θ = 0 Given data: Diameter of glass tubes d1 = 7mm = 0.007 m Diameter of glass tube d2 = 9mm = 0.009 m Range of manometer reading = 50 mm to 170 mm = 0.05m to 0.17m Surface tension σ = 0.090 N/m Angle of contact θ = 0 To find: Percentage of error Solution: h1 - h2 = 0.005242 – 0.00407 = 0.001172 m 4. Percentage error at highest reading = (0.001172/0.17) × 100 = 0.6894 % 5. Percentage error at lowest reading = (0.001172/0.05) × 100 = 2.34 % Result : Manometer percentage error at highest reading is 0.6894% and manometer percentage error at lowest reading is 2.34% Example - 42 The surface tension of water in contact with air is 0.0235N/m. The pressure inside a droplet of water is to be 20N/m2. Calculate the diameter of the droplet of the water. Given data: Surface tension of water (σ) = 0.0235N/m. The pressure of droplet of water = 20N/m2 To find: Diameter of the droplet of the water (d) Solution: The pressure of droplet of water (p) = 4 σ/ d d = 4 σ /p d = 4 × 0.0235/20 d = 0.0047m d = 4.7mm Result : Diameter of the droplet of the water (d) = 4.7mm Example - 43 Find the surface tension of the soap bubble of 100mm diameter when the inside pressure is 5N/m2 above the atmospheric pressure. Given data: Soap bubble of diameter(d) = 100mm = 0.1m Inside pressure(p) = 5N/m2 To find: Surface tension of the soap bubble (σ) Solution: Pressure of the soap bubble (p) = 8 σ/d σ = p × d/8 = 5 × 0.1/8 σ = 0.0625 N/m Result : Surface tension of the soap bubble (σ) = 0.0625N/m Example - 44 The pressure outside the droplet of water of diameter 10mm is 10.32 N/cm2 (at atmospheric pressure). Calculate the pressure within the dropt if surface tension is given as 0.0425 N/m of water. Given data: Diameter of droplet, d = 10mm = 0.01m Pressure outside the droplet = 10.32 N/cm2 = 10.32 × 104 N/m2 Surface tension, σ = 0.0425 N/m To find: Pressure inside the droplet Solution: The pressure inside the droplet, in excess of outside pressure is given by = 17 N/m2 Pressure inside the droplet = P + pressure outside the droplet or atmospheric pressure = 17 + 10.32 × 104 = 103.217 × 103 N/m2 Result: Pressure inside the droplet = 103.217 × 103 N/m2 Example - 45 Calculate the gauge pressure and absolute pressure within a droplet of water 0.6 cm diameter and jet of water 0.9cm in diameter. Assume the surface tension of water as 0.06 N/m and the atmospheric pressure as 101.3 KN/m2. Given data: Surface tension of water σ = 0.06 N/m Atmospheric pressure P = 101.3 × 103 N/m2 Diameter of water droplet d = 0.6 cm = 0.006m Diameter of water jet d = 0.9 cm = 0.009m To find: Gauge pressure and absolute pressure 1. Water droplet 2. Jet of water Solution : (i) Gauge pressure of water droplet = 40 N/m2 (ii) Absolute pressure of water droplet = 101.34 × 103 N/m2 (iii) Gauge pressure of set of water = 13.33 N/m2 (iv) Absolute pressure of set of water = 101.33 × 103 N/m2 Example - 46 A capillary tube having inside diameter 6mm is dipped in CCl4 at 20°C. Find the rise of CCl4 in the tube if surface tension is 2.67 N/m and specific gravity is 1.594 and contact angle θ is 60° and specific weight of water at 20°C is 9981 N/m3. Given data: Diameter of tube, d = 6mm = 0.006m Specific gravity of CCl4 = 1.594 Specific weight of water = 9981 N/m3 Surface tension, σ = 2.67 N/m Contact angle θ = 60° To find: Capillary rise of CCl4 Solution : Specific weight of CCl4 = Sp.gravity × Sp.wt of water = 1.594 × 9981 = 15909.714 N/m3 w = 15909.714 N/m3 = 0.05594 m = 55.94 mm Result : Capillary rise of CCl4 = 55.94 mm1. Density:
2. Specific weight:
 The specific weight of the water at the standard temperature of 4°c is 9810 N/m3 (or) 9.81KN/m3.
The specific weight of the water at the standard temperature of 4°c is 9810 N/m3 (or) 9.81KN/m3.3. Specific volume:
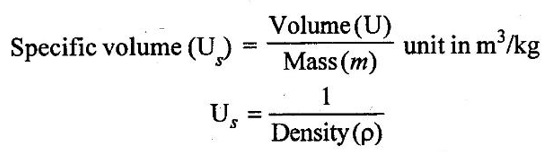
4. Specific gravity:

5. Solved Examples based on Fluids property:


6. Viscosity:
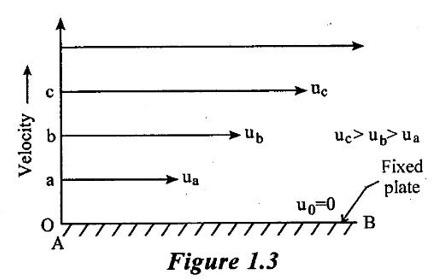


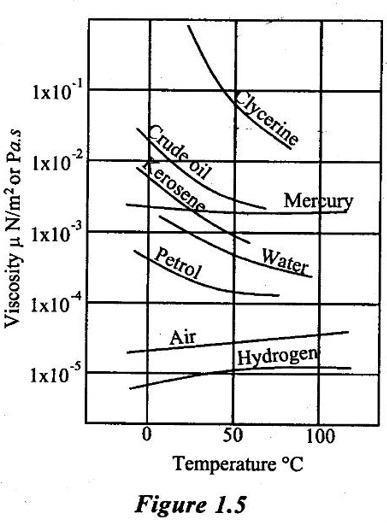
 Result :
Result :




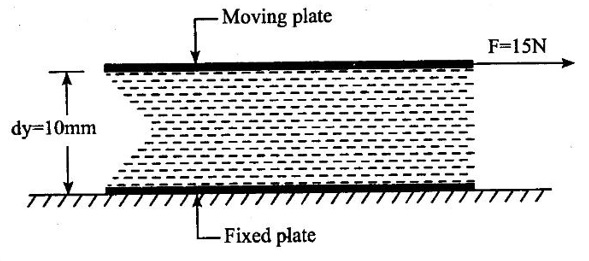
 (i) Change of velocity(du) = u1 – u2 [Not change in velocity. so u2 = 0 & u1 = u]
(i) Change of velocity(du) = u1 – u2 [Not change in velocity. so u2 = 0 & u1 = u]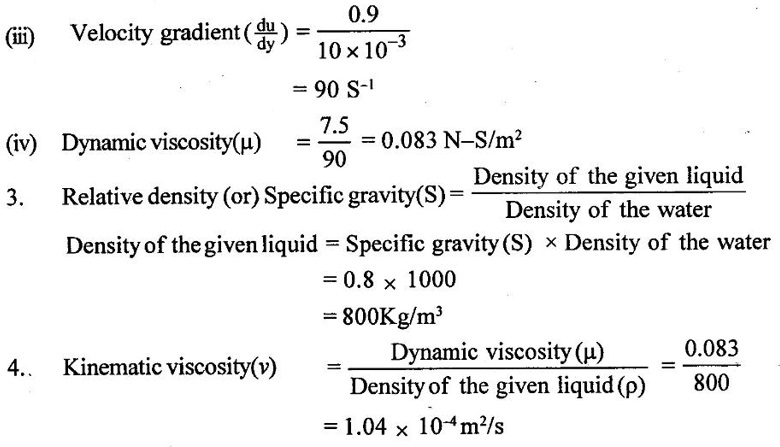




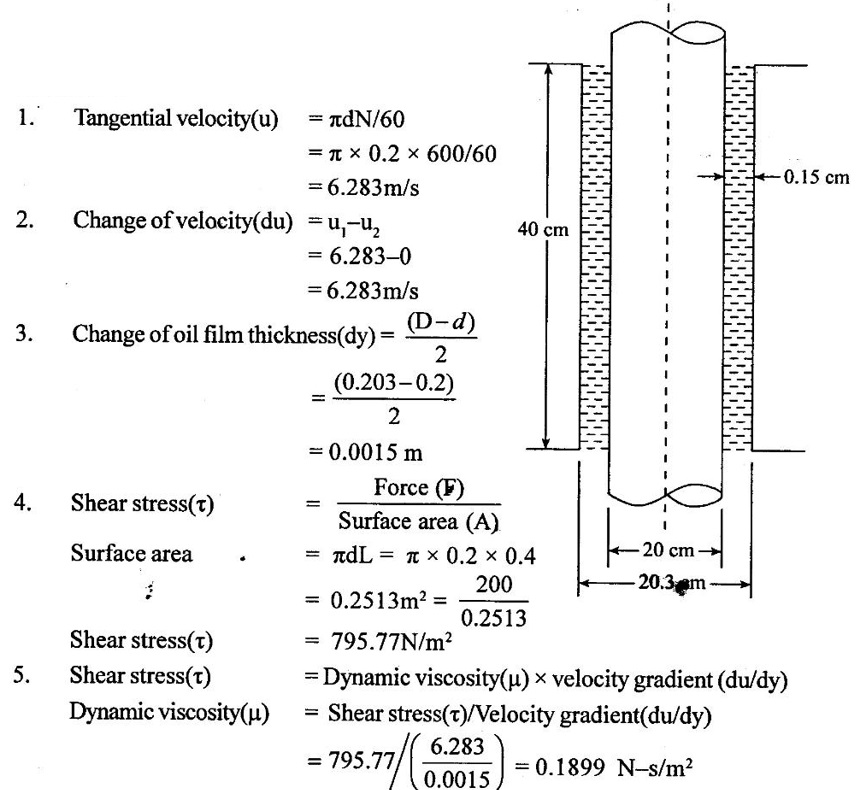 Result :
Result :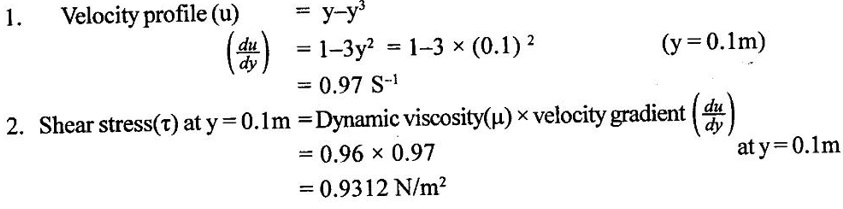 Result :
Result :

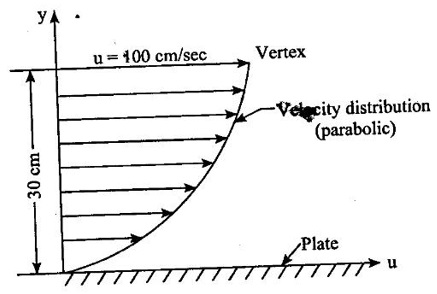


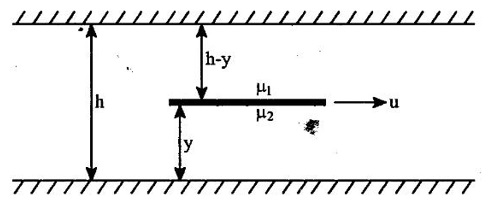
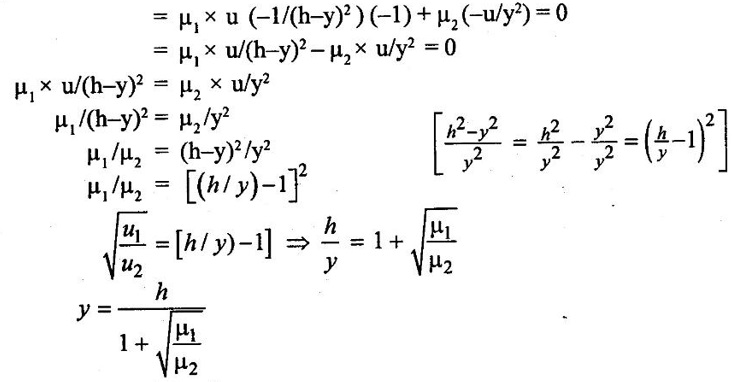


 Given data:
Given data: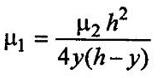
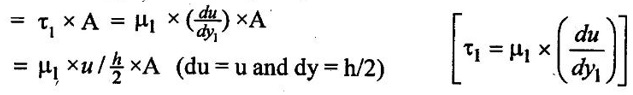
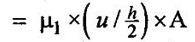
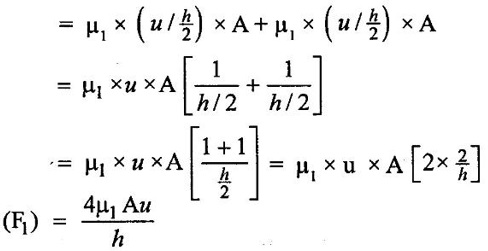

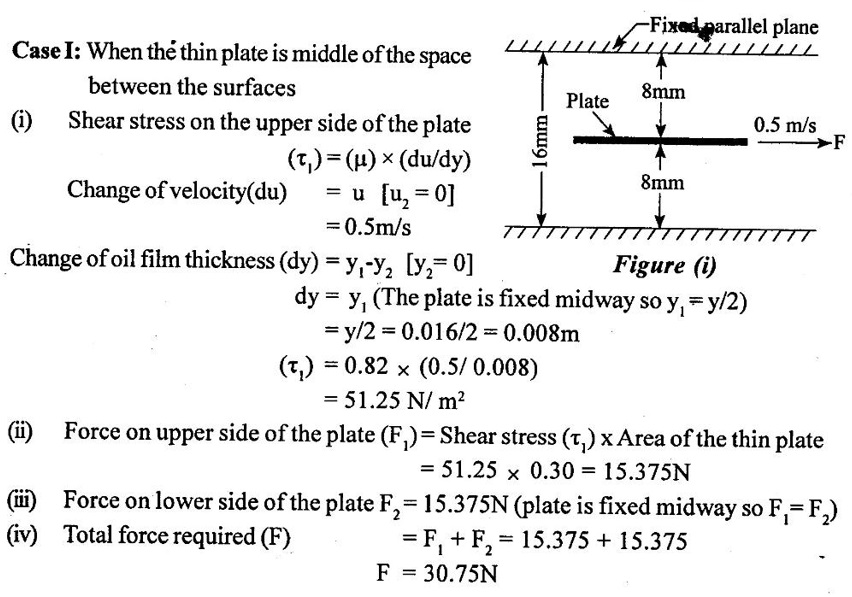
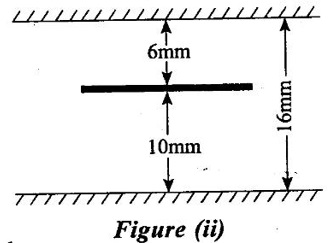
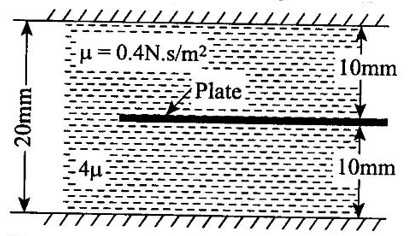

 3. Shear stress on the left side of the plate (τ1) = (μ) × (du/dy)1
3. Shear stress on the left side of the plate (τ1) = (μ) × (du/dy)1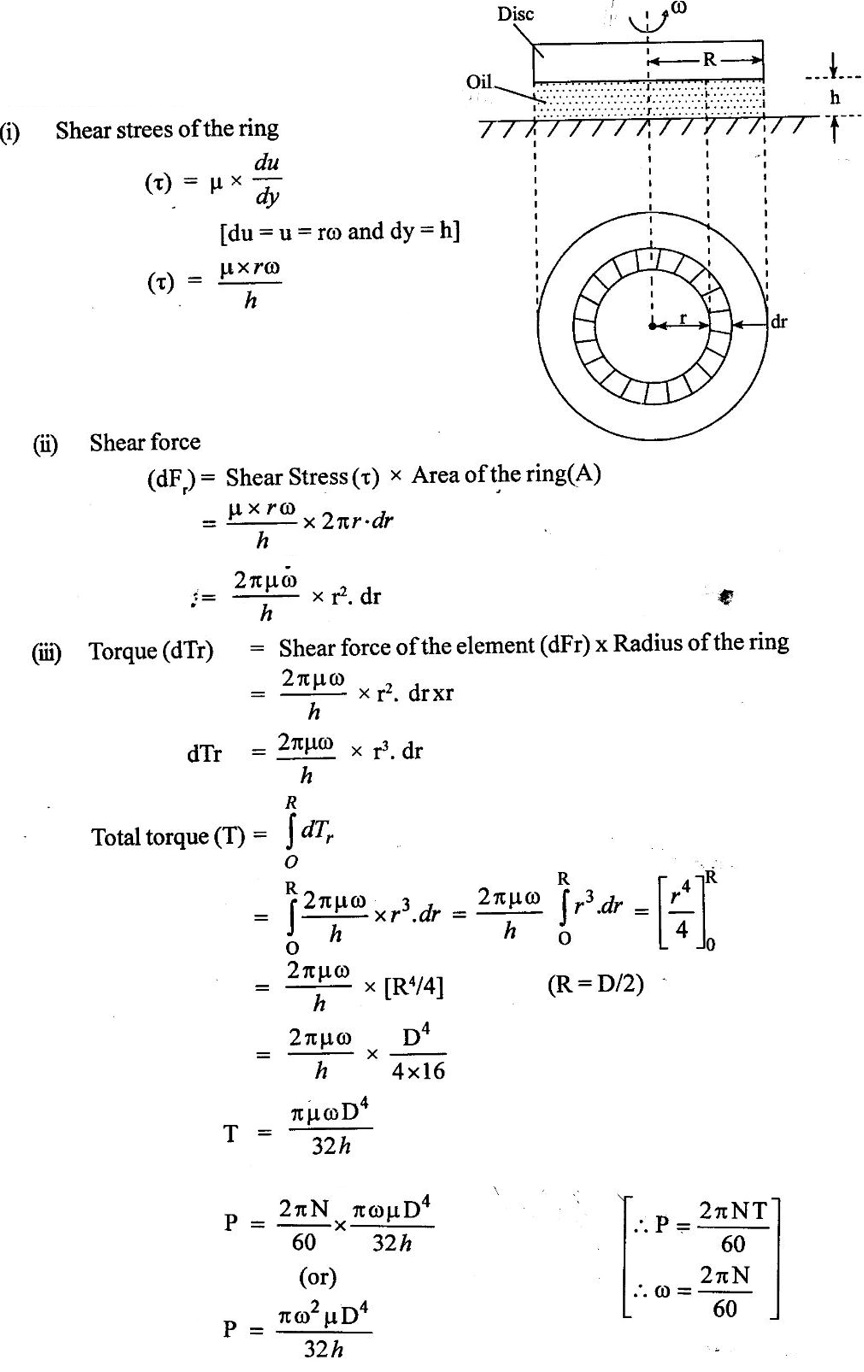

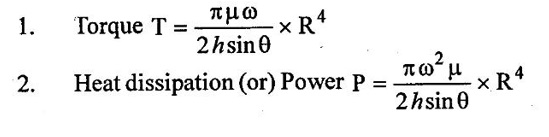
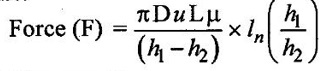
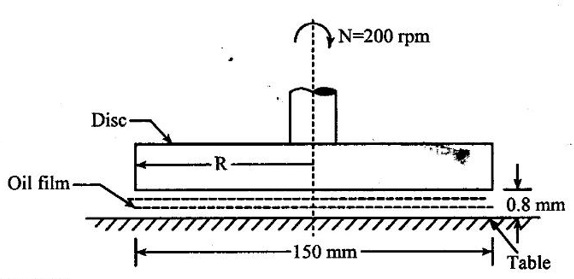
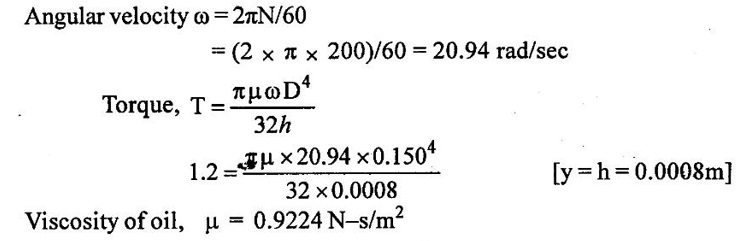
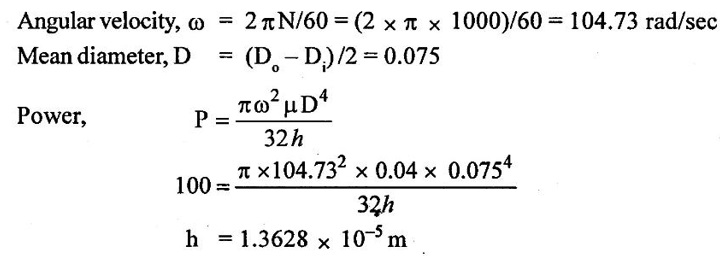 Result :
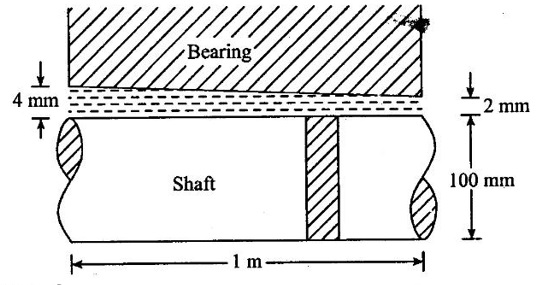
Result :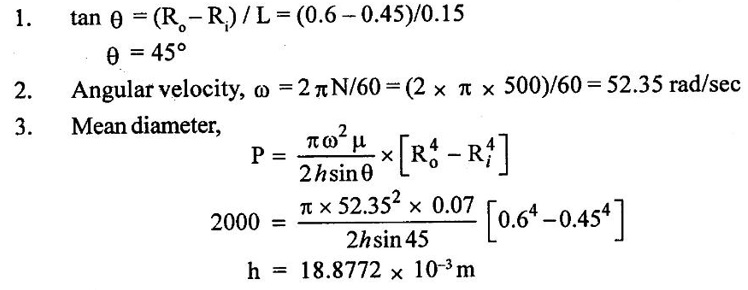
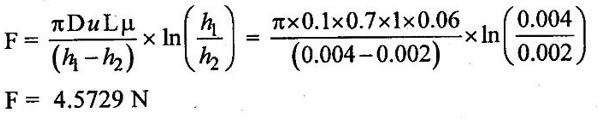
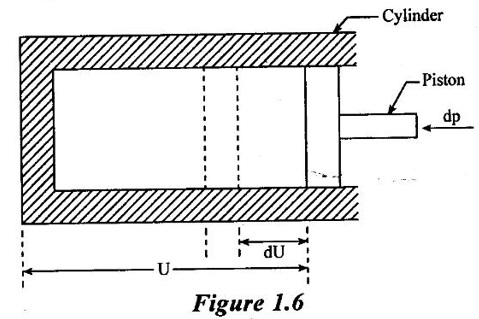
7. Compressibility:
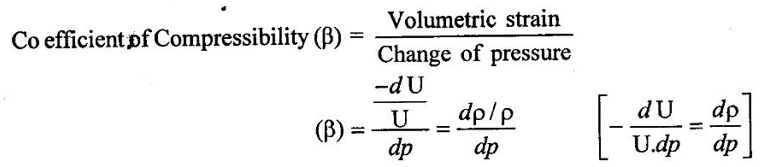
8. Bulk modulus (K):
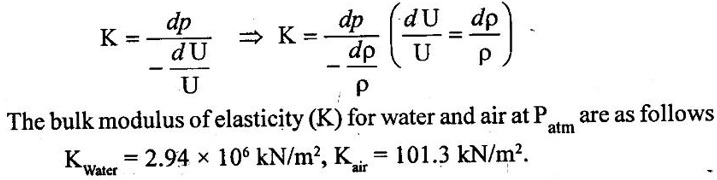
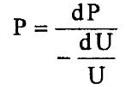
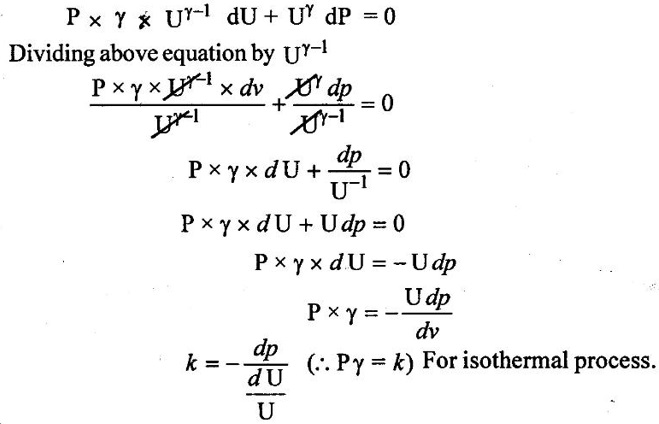
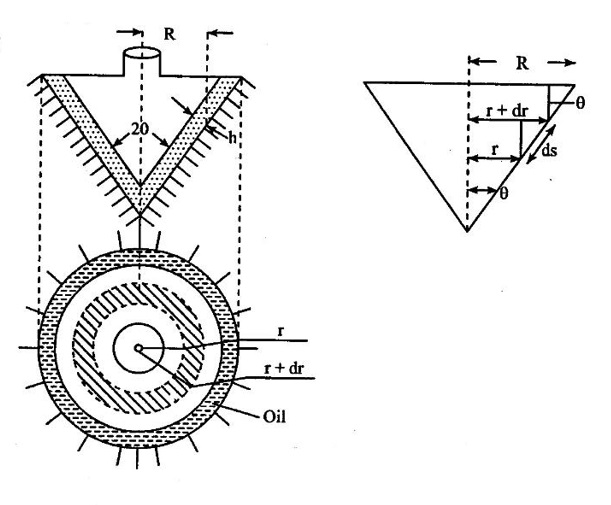
9. Surface tension:

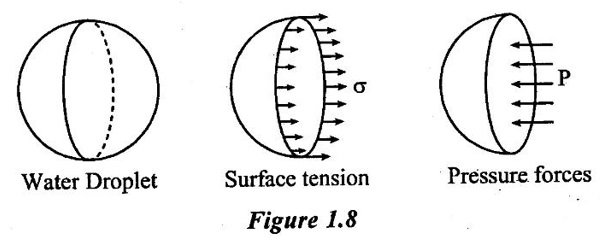
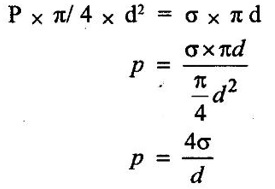
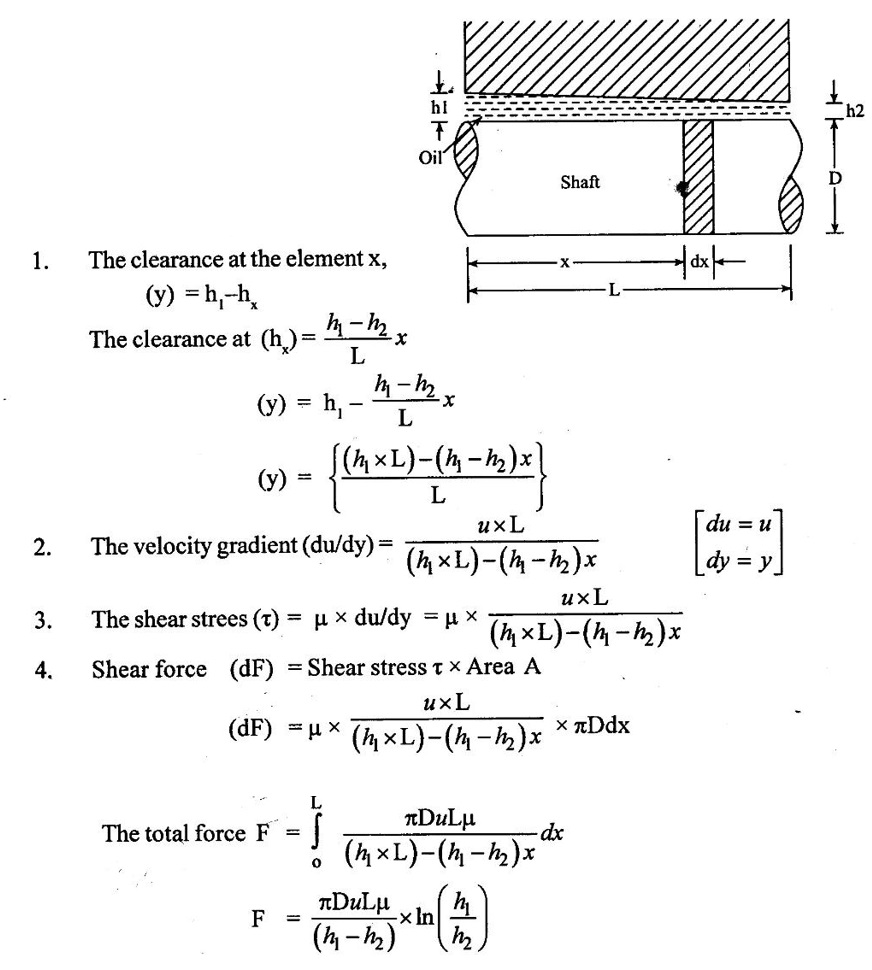
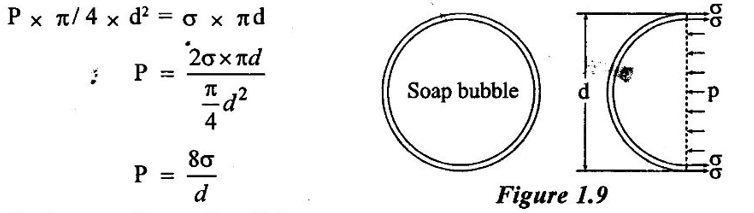 3. Surface tension on liquid jet:
3. Surface tension on liquid jet:
10. Capillarity (or) meniscus:
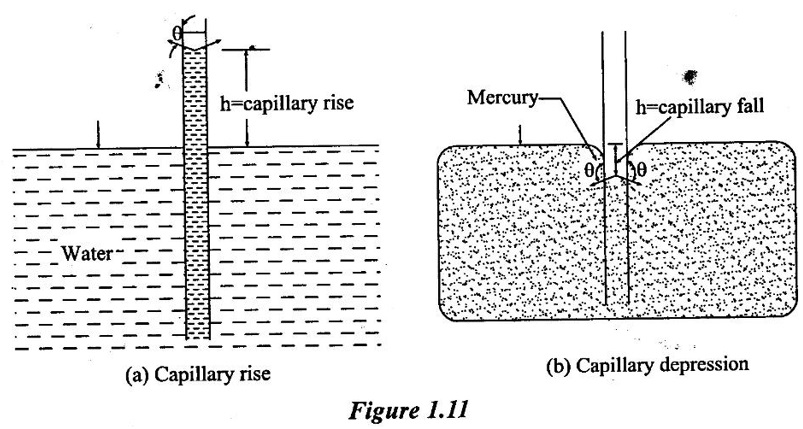
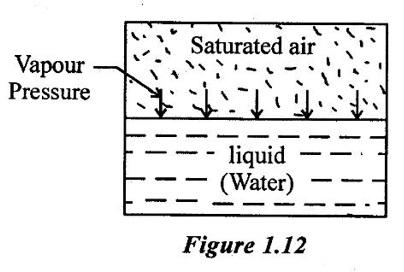
11. Vapour pressure:
12. Solved Examples based on bulk modulus and Compressibility:
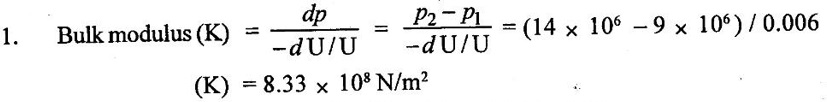 2. Co-efficient of compressibility(β) = 1/K = 1/8.33 × 108
2. Co-efficient of compressibility(β) = 1/K = 1/8.33 × 10813. Solved Examples based on capillarity:

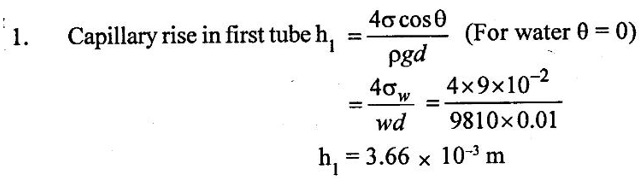
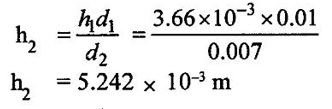
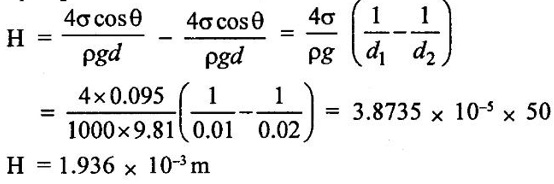
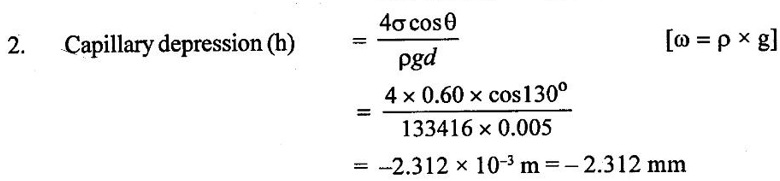
 3. Error in pressure measurement due to capillary action
3. Error in pressure measurement due to capillary action14. Solved Examples based on surface tension:
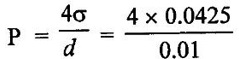
 Result:
Result: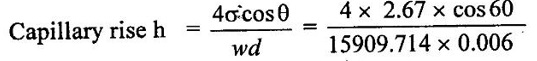
Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics : Tag: : with Solved Example Problems - Properties of Fluids
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
