Basic Electrical and Electronics Engineering: Unit I: Electrical Circuits
Problems on Matrix Method of Analysis
Electrical Circuits
Problems on Matrix Method of Analysis with solution: Basic Electrical and Electronics Engineering: Electrical Circuits
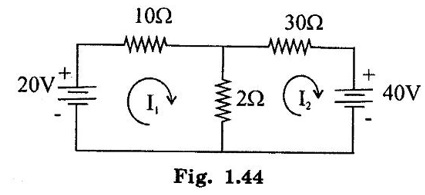
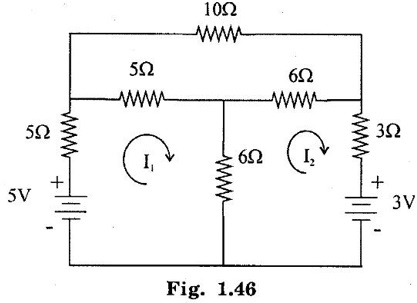
PROBLEMS ON MATRIX METHOD OF ANALYSIS Problem 1.14 Find the current through 2Ω resistor in network of figure 1.43 by mesh method. Also find the power supplied by the batteries. Solution : Apply KVL to both loops, 10I1 + 2 (I1 – I2) = 20 12 I1 -2 I1 = 20 …. .. (1) 2 (I2 − I1) + 30 I2 = −40. −2 I1 + 32 I2 = −40 ...... (2) Using the above 2 equations, form the matrix equation, Here we have to solve the mesh currents I1 and I2. By applying Cramer's rule, We can obtain mesh currents. Current through 2Ω resistor = I1 – I2 = 2.627 A Power supplied by 20V source = 20 × 1.47 = 29.4 W Power supplied by 40V source = 40 × -1.157 = -46.28 W. = 46.28 W (positive value considered) Problem 1.15 Find the current I which flows through 10 Ω resistor in the circuit shown in figure 1.45. Solution : Apply KVL, to obtain mesh equations. In loop: + 30I1 + 30 (I1 – I2) = 90 60 I1 - 30 I2 = 90 …. (1) In loop 2: + 10 I2 + 30 (I2 − I1) + 30 (I2 − I3) = 0 10 I2 + 30 I2 - 30 I1 + 30 I2 - 30 I3 = 0 -30 I1 + 70 I2 - 30 I3 = 0 30 I1 - 70 I2 + 30 I3 = 0 ….(2) In loop 3 : 30I3 + 30 (I3 – I2) + 30 I3 = 0 - 30 I2 + 90 I3 = 0 30 I2 - 90 I3 = 0 .....(3) Using above equations form the matrix equations By applying Crammer's rule, we can obtain mesh current I2 = 60 [(-70 × −90) - (30 × 30)] - (-30) [(30 × −90) – 0]. = 60 [(6300 -900)] + 30 [-2700] = 243000. Therefore, current through 10 Ω resistor is 1A. Problem 1.16 Find the current through the 10 Ω resistor in network of figure 1.46 by mesh method. Solution : Apply kVL in loop 1. 5I1 + 5 (I1 – I3) + 6 (I1 − I2) = 5 5 I1 + 5 I1 - 5 I3 + 6 I1 − 6 I2 = 5 16 I1 - 6 I2 - 5 I3 = 5 ... (1) In loop 2: 6 (I2 – I3) + 6 (I2 − I1) + 3 I2 = -3 6 I2 − 6 I3 + 6 I2 − 6 I1 + 3 I2 = -3 -6 I1 + 15 I2 - 6 I3 = -3 ……(2) In loop 3: 5 (I3 − I1) + 6 (I3 − I2) + 10 I3 = 0 5 I3 - 5 I1 + 6 I3 - 6 I2 + 10 I3 = 0 -5 I1 - 6 I2 + 21 I3 = 0 ……(3) Mesh matrix : = 16 [(15 × 21) − (−6 × −6)] (-6 × -6)] - (-6) [(-6 × 21) − (−5×-6)] - 5 [(-6 × −6) − (−5 × 15)] = 16 [315 - 36] + 6 [-126 - 30] 5 [36 + 75] = 16 × 279 + 6(−156) 5 (111) = 4464 - 936 – 555 = 2973 = 16 [0 - (18)] − (−6) [0 − (15)] + 5 [36 − (−75)] = -288 - 90 + 555 = 177Mesh Method / Loop Method




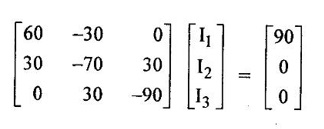
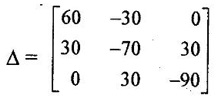
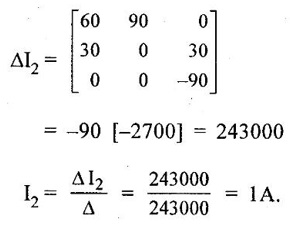
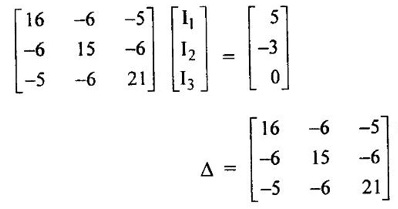

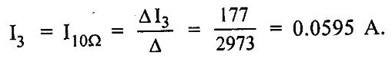
Basic Electrical and Electronics Engineering: Unit I: Electrical Circuits : Tag: : Electrical Circuits - Problems on Matrix Method of Analysis
Related Topics
Related Subjects
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation

