Engineering Physics: Unit II: Electromagnetic Waves
Phase and Orientation of Electromagnetic wave in matter
From the equations (13) and (14), it is clear that the phases of electric and magnetic fields are same (ie., ωt - kx).
PHASE AND ORIENTATION OF EM WAVE IN MATTER From the equations (13) and (14), it is clear that the phases of electric and magnetic fields are same (ie., ωt - kx). Thus, both fields are in phase with each other. We know for electromagnetic waves in free space The relation between their time and space variations is given from Maxwell's equation We know that Substituting Ey and Hz from the equations (1) & (2) in eqn. (3), we get This is the relation between the electric field vector and magnetic field vector. I is determined by the μ0 and ε0. This ratio of the electric and magnetic vectors is directly professional to the square root of the ratio of μ0 and ε0. It shows that the value of electric field at any instant is about 377 times the value of magnetic vector in electromagnetic wave. The ratio E/H is having the unit of impedance (Resistance) ie., ohm. Therefore, the quantity It is known as intrinsic or characteristic impedance of free space, denoted by Z0. It is a constant quantity for free space and having value = 377Ω. The above discussion shows that the vector Thus if Further, The cross product of electric field vector An electro-magnetic wave has electric and magnetic field vectors oscillating perpendicular to each other. The electric and magnetic disturbance travels in a same direction perpendicular to both the electric and magnetic vectors. Let a plane polarized electromagnetic wave be propagating along the x-axis. The electric vector is directed along the y-axis, then the magnetic vector is directed along the z-axis. Hence, But Ey Hz measures the energy per second (ie power) per unit area. Hence In other words, Poynting vector gives the time rate of flow of electromagnetic wave energy per unit area of the medium. Further the average Poynting vector for one complete cycle of electromagnetic wave is given by 1. If there is a varying electric field in vacuum, there is also a varying magnetic field and vice versa. The electric and magnetic fields are perpendicular to each other and also perpendicular to the direction of propagation of the wave. 2. The electric and magnetic fields obey wave equation with identical propagation speeds. 3. The speed of propagation given by c = 4. The light waves can, therefore, be identified as electromagnetic waves. 5. The electric and magnetic fields in electromagnetic waves oscillate in phase with each other. Relation between electric and magnetic field vectors
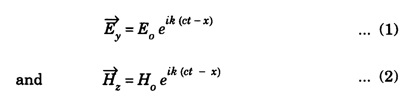
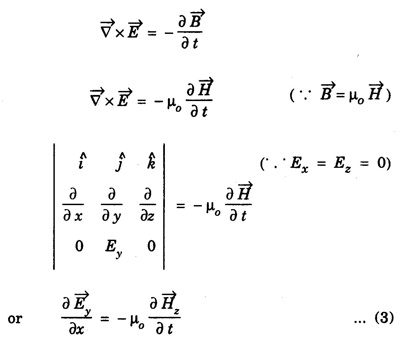


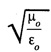 has the dimensions of impedance.
has the dimensions of impedance.
![]() and the vector
and the vector ![]() are at right angle to each other and the wave propagates in the direction of
are at right angle to each other and the wave propagates in the direction of  (Fig. 2.5)
(Fig. 2.5)![]() is parallel to Y . axis. The vector
is parallel to Y . axis. The vector 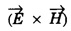 is known as Poynting vector after J.S. Poynting who first investigated its properties.
is known as Poynting vector after J.S. Poynting who first investigated its properties.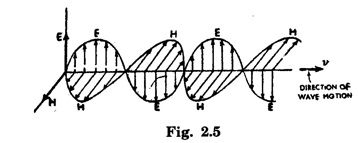
![]() and
and ![]() are always in the same phase, i.e., their relative magnitudes are the same at all points and at all times.
are always in the same phase, i.e., their relative magnitudes are the same at all points and at all times.Poynting Vector
![]() and the magnetic field vector
and the magnetic field vector ![]() is called poynting vector. It is denoted by
is called poynting vector. It is denoted by 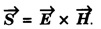
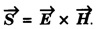
![]() represents the energy propagating along the x-axis in Js-1m-2 or Wm-2.
represents the energy propagating along the x-axis in Js-1m-2 or Wm-2.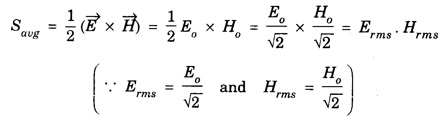
Maxwell's findings is summarised as below.
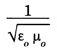 is the same as the measured speed of light.
is the same as the measured speed of light.
Engineering Physics: Unit II: Electromagnetic Waves : Tag: : - Phase and Orientation of Electromagnetic wave in matter
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
