Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics
Pascal's Law
Definition, Statement, Formula, Derivation
Pascal's law states that the pressure or intensity of pressure at a point in a static fluid is equal in all directions.
PASCAL'S LAW Pascal's law states that the pressure or intensity of pressure at a point in a static fluid is equal in all directions. Consider an arbitrary fluid element of wedge shape in a fluid mass at rest as shown in fig 1.16. The fluid element is of very small dimensions dx, dy and ds. Let the width of the element perpendicular to the plane of paper is unity and Px, Py and Pz are the pressure or intensity of pressure acting on the face AB, AC & BC respectively. Let ∠ ABC = θ. Then the forces acting on the element are: 1. Pressure forces normal to the surfaces, and 2. Weight of element in the vertical direction The forces on the faces are: Force on the face AB = Px + Area of face AB = Px × dy × 1 Similarly Force on the face AC = Py × dx × 1 Similarly Force on the face BC = Pz × ds × 1 Weight of element = (Mass of element) × g Where ρ = density of fluid Resolving the forces in x-direction, Px X dy × 1 - P (ds × 1) sin (90° – θ) = 0 Px X dy × 1 - Pz ds × 1 cos θ = 0 From fig 1.16, ds cos θ = AB = dy Px × dy × 1 - Pz X dy × 1 = 0 Px = Pz Similarly, resolving the forces in y - direction. But ds sin θ = dx and also the element is very small and hence weight is negligible. Pydx - Pz × dx = 0 Py = Pz Px = Py = Pz The above equation shows that the pressure at any point in x, y and z direction is equal. Since the choice of fluid element was completely arbitrary, which means the pressure at any point is the same in all directions.
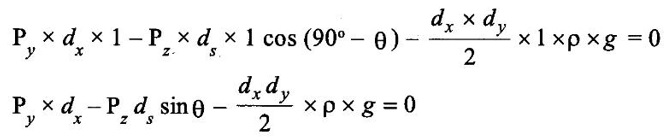
Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics : Tag: : Definition, Statement, Formula, Derivation - Pascal's Law
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
