Engineering Mechanics: Unit III: Distributed Forces
Parallel Axes Theorem (Area Moment of Inertia)
Statement, Proof, Diagram, Equation
The moment of inertia of any area about an axis in its plane is the sum of moment of inertia about a parallel axis passing through the centroid of the area
Parallel Axes Theorem • Statement: The moment of inertia of any area about an axis in its plane is the sum of moment of inertia about a parallel axis passing through the centroid of the area (known as centroidal axis) and the product of area and square of the distance between the two parallel axes. • Proof : Consider an area A with centroid G as shown in Fig. 6.4.1. To find moment of inertia about AB, consider an area element dA at distance y as shown. • Let CD be an axis parallel to AB passing through the centroid G of the area A. • Let d be the distance between the two parallel axes AB and CD and y1, the distance of dA from centroidal axis. By definition, The moment of inertia of the area A about centroidal axis CD is ∫y1dA is the moment of area A about its centroidal axis. As area is always symmetrical about its centroidal axis, Substituting these in equation (6.4.1) IAB = IG + 0 + d2 A This proves the parallel axes theorem.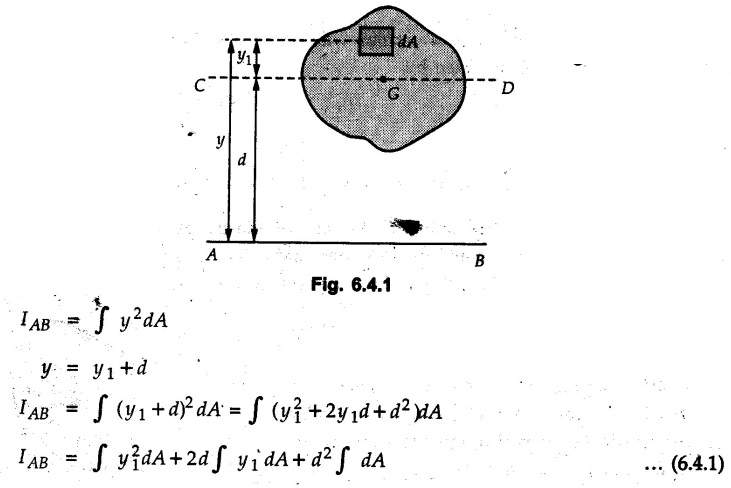
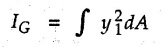
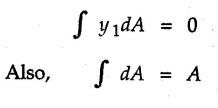

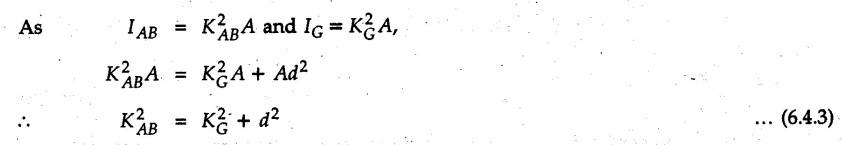
Engineering Mechanics: Unit III: Distributed Forces : Tag: : Statement, Proof, Diagram, Equation - Parallel Axes Theorem (Area Moment of Inertia)
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
